以下是数据结构中关于广度优先遍历无向连通图的操作(编程风格参考严蔚敏版数据结构)。
其实深度优先遍历就是二叉树的层次遍历的推广。
头文件及宏
#include<iostream>
#include<stdio.h>
using namespace std;
typedef char VerTexType;
typedef int ArcType;
typedef VerTexType QElemType;
#define MaxInt 32767
#define MVNum 100
#define OK 1
#define ERROR -1;
typedef int status;
说明:typedef VerTexType QElemType;//队列元素的类型就是节点的类型
队列及图的结构体声明:
typedef struct{
VerTexType vexs[MVNum] {'A','B','C','D','E','F','G','H'};//节点表
ArcType arcs[MVNum][MVNum];//邻接表(肯定是个正方形的矩阵)
int vexnum = 8,arcnum = 9;//该邻接矩阵的节点数、边数
}AMGraph;
typedef struct SeQueue{
QElemType *base;
int front;//标记队头
int rear;//标记队尾
}Squeue;
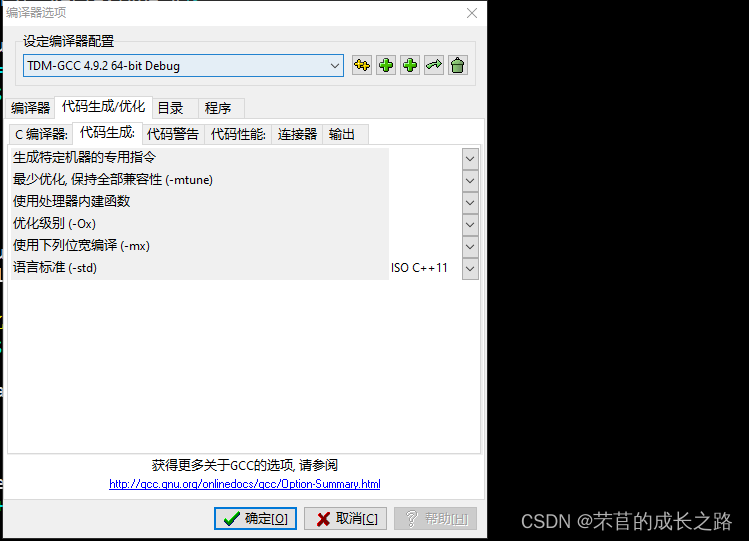
说明:直接声明节点表,编译器可能会报警告。这个影响不大,这个是编译器C++版本老旧的问题。如果是使用DEV-C++软件编译的话,可以去这样设置一下:工具 -> 编译选项 -> Setting -> 代码生成/优化 -> 代码生成 -> 语言标准(-std),选ISO C++11。
关于图和队列的基本操作
关于图和队列的基本操作在前面的文章里有整理,为了不让篇幅冗余和重复啰嗦,有需要的读者可以去往期帖子里获取:
数据结构——深度优先遍历(DFS)无向连通图
数据结构——顺序队列1(声明、初始化、判断队空/队满、入队、出队、遍历队)
广度优先遍历(BFS)核心代码
void BFS(AMGraph &G,Squeue &Q,VerTexType v){
int vi = LocateVex(G,v);
cout<<v<<" ";visited[vi] = true;//被访问过设true
Enqueue(Q,v);//被访问过的节点入队
while(isNotEmpty(Q)!=-1){//-1表示队空
VerTexType vh = Dequeue(Q);// 队头元素
for(int vn = FirstAdjVex(G,vh);vn>=0;vn = NextAdjVex(G,vh,vn)){//获取全部邻接节点
if(!visited[vn]){
VerTexType V = Transform(G,vn);//通过下标寻找节点
cout<<V<<" ";visited[vn] = true;
Enqueue(Q,V);//被访问的节点入队
}//if
}//for
} //while
}
代码说明:
当访问了某个节点后,先获取其全部邻接节点(记录方式为入队),然后再将全部邻接节点依次输出。重复上述过程,就完成了广度优先遍历。
把它转换成二叉树来看,就是这么个情况:先获取其全部子节点(就是对应图的邻接节点),然后将每个子节点挨个输出,每访问一个子节点就把该子节点的子节点全部找出来(以入队的方式记录),重复以上过程。
举个例子:
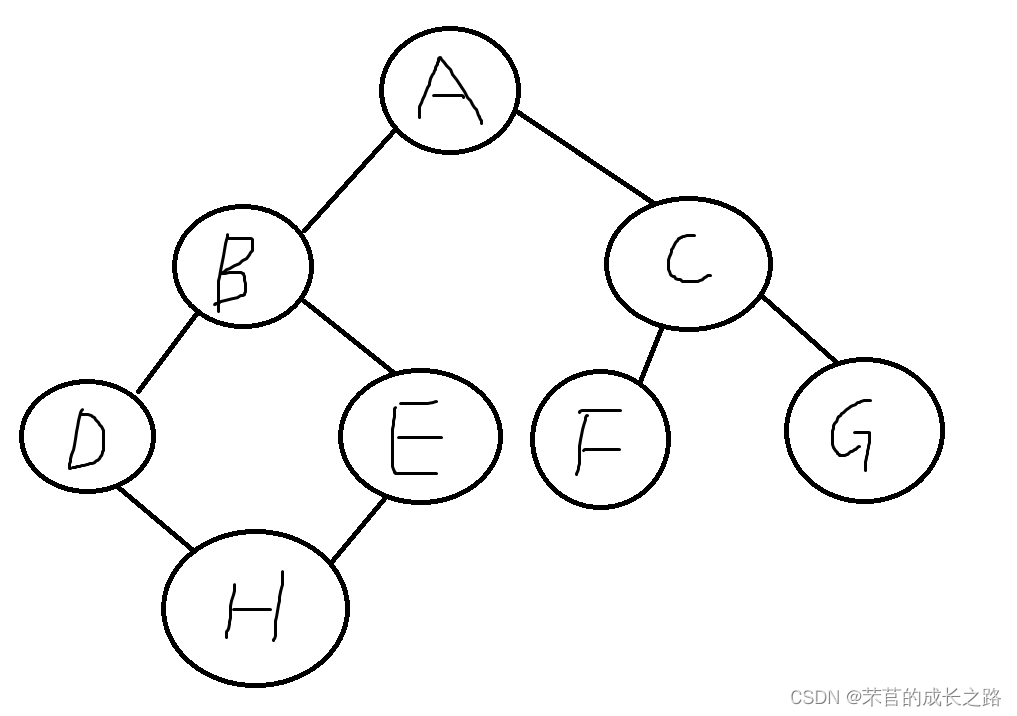
那么广度优先遍历是如何遍历的呢?
从A开始:访问A(输出A),A标记已访问,A入队;
进入while循环:
A出队(因为此时A作为队头节点),然后进入for循环(这个循环的作用是找出A全部邻接节点)
A的邻接节点B没被访问过,访问B(输出B)。然后B节点入队;
A的邻接节点C没被访问过,访问C(输出C)。然后C节点入队;此时队列是[B,C]。
此时队头是B,B出队。再次执行for循环(此次for循环就是找出B的全部邻接节点)
B的邻接节点D没被访问过,访问D(输出D)。然后D节点入队;
B的邻接节点E没被访问过,访问E(输出E)。然后D节点入队。此时队列是[C,D,E]。
此时队头是C,C出队,再次执行for循环。
C的邻接节点F没被访问过,访问F(输出F),然后F节点入队;
C的邻接节点G没被访问过,访问G(输出G),然后G节点入队。此时队列是[D,E,F,G]。
此时队头是D,D出队,再次执行for循环:
D的邻接节点H没被访问过,访问H(输出H)。然后H节点入队。此时队列是[E,F,G,H]。
往后就是队列元素依次出队寻找邻接节点,但是此时它们的邻接节点都已被访问过,找到了也不会输出了。直到队列为空,程序结束。
所以输出结果就是A B C D E F G H。
运行结果

源代码:
#include<iostream>
#include<stdio.h>
using namespace std;
typedef char VerTexType; //代表节点变量的类型(一般我们用ABCD表示节点,所以用char)
typedef int ArcType; // 代表边变量的类型(肯定用长度表示边呀,所以用int或者double都可)
typedef VerTexType QElemType;//队列元素的类型就是节点的类型
#define MaxInt 32767 //边的最大值(表示目标不可达)
#define MVNum 100 //最大节点数
#define OK 1
#define ERROR -1;
typedef int status;
bool visited[MVNum];//标记访问记录的数组;宏定义会自动赋值为0
typedef struct{
VerTexType vexs[MVNum] {'A','B','C','D','E','F','G','H'};//节点表
ArcType arcs[MVNum][MVNum];//邻接表(肯定是个正方形的矩阵)
int vexnum = 8,arcnum = 9;//该邻接矩阵的节点数、边数
}AMGraph;
typedef struct SeQueue{
QElemType *base;
int front;//标记队头
int rear;//标记队尾
}Squeue;
int LocateVex(AMGraph G, VerTexType v){
int i;
for(i=0;i<G.vexnum;i++){
if(G.vexs[i]==v){
return i;
}
}
return ERROR;
}
status initialQ(Squeue &sq){
sq.base = new QElemType[MVNum];
if(!sq.base){
cout<<"初始化失败\n";
return ERROR;
}
sq.front = sq.rear = 0;
return OK;
}
status Enqueue(Squeue &sq,QElemType e){
sq.base[sq.rear++] = e;
return OK;
}
VerTexType Dequeue(Squeue &sq){
VerTexType e = sq.base[sq.front];
for(int i=sq.front;i<sq.rear-1;i++){
sq.base[i] = sq.base[i+1];
}
sq.rear--;
return e;
}
status isNotEmpty(Squeue sq){
if(sq.front==sq.rear){
// cout<<"队空!\n";
return ERROR;
}
return OK;
}
status CreateUDN(AMGraph &G){//创建无向图
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++){
if(i==j){
G.arcs[i][j] = 0;
}else
G.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达
}
}
G.arcs[0][1]=1;
G.arcs[0][2]=1;
G.arcs[1][3]=1;
G.arcs[1][4]=1;
G.arcs[2][5]=1;
G.arcs[2][6]=1;
G.arcs[3][7]=1;
G.arcs[4][7]=1;
G.arcs[5][6]=1;
for(int i=0;i<G.vexnum;i++){
for(int j=i+1;j<G.vexnum;j++){
if(G.arcs[i][j]==1){
G.arcs[j][i] = 1;
}
}
}//矩阵对称
return OK;
}
void ShowGraph(AMGraph G){
cout<<" ";
for(int i=0;i<G.vexnum;i++){
cout<<" "<<G.vexs[i];
}
cout<<endl;
for(int i=0;i<G.vexnum;i++){
cout<<G.vexs[i]<<" ";
for(int j=0;j<G.vexnum;j++){
if(G.arcs[i][j]==MaxInt){
cout<<"* ";
}else{
cout<<G.arcs[i][j]<<" ";
}
}
cout<<endl;
}
}
VerTexType Transform(AMGraph G, int vn){
return G.vexs[vn];
}
int FirstAdjVex(AMGraph G,VerTexType v){//v的第一个邻接点
int vi = LocateVex(G,v);
for(int i=0;i<G.vexnum;i++){
if(!visited[i]&&G.arcs[vi][i]==1){
return i;//找到邻接点且此邻接点未被访问过
}
}
return ERROR;//未找到邻接点
}
int NextAdjVex(AMGraph G,VerTexType v ,int vn){//v相对于vn的下一个邻接点
int vi = LocateVex(G,v);
for(int i=vn+1;i<G.vexnum;i++){
if(!visited[i]&&G.arcs[vi][i]==1){
return i;//找到邻接点且此邻接点未被访问过
}
}
return ERROR;//未找到下一个邻接点
}
void BFS(AMGraph &G,Squeue &Q,VerTexType v){
int vi = LocateVex(G,v);
cout<<v<<" ";visited[vi] = true;//被访问过设true
Enqueue(Q,v);//被访问过的节点入队
while(isNotEmpty(Q)!=-1){//-1表示队空
VerTexType vh = Dequeue(Q);// 队头元素
for(int vn = FirstAdjVex(G,vh);vn>=0;vn = NextAdjVex(G,vh,vn)){//获取全部邻接节点
if(!visited[vn]){
VerTexType V = Transform(G,vn);//通过下标寻找节点
cout<<V<<" ";visited[vn] = true;
Enqueue(Q,V);//被访问的节点入队
}//if
}//for
} //while
}
int main(){
AMGraph G;
Squeue Q;
initialQ(Q);
CreateUDN(G);
ShowGraph(G);
BFS(G,Q,'A');
return 0;
}
代码是参考严蔚敏版《数据结构》写的,因为书上只写核心代码不是完整的源程序,以上代码能调是通过是自己对书本代码进行补充才能跑起来,水平有限可能有错,敬请批评指正。