22.10.30 LC周赛 哈希表+排序、map巧用、树+两遍DFS
?? 这次周赛仍然只做出1道题,而且第二题绊住好久,还是动态规划掌握的不好,这周没怎么做题,只做了做每日一题,还是不太够的!不多说了,保持激昂的精神继续努力啊!这次学到不少知识,分享记录一下,如果朋友看得喜欢麻烦点赞收藏哦。
? 部分代码参考了其他选手的代码,提前说一声,这并不都是我自己码出来的。~~
6220. 可被三整除的偶数的平均值(反向思维)
题目链接:6220. 可被三整除的偶数的平均值
题目大意:给你一个由正整数组成的整数数组 nums ,返回其中可被 3 整除的所有偶数的平均值。
注意:n 个元素的平均值等于 n 个元素 求和 再除以 n ,结果 向下取整 到最接近的整数。
例如:
输入:nums = [1,3,6,10,12,15]
输出:9
解释:6 和 12 是可以被 3 整除的偶数。(6 + 12) / 2 = 9 。
输入:nums = [1,2,4,7,10]
输出:0
解释:不存在满足题目要求的整数,所以返回 0 。
- 解题思路:简单题不说了 其实可以再简单些 直接 % 6 .
- 时间复杂度: O ( N ) O(N) O(N) N为数组长度
- 空间复杂度: O ( 1 ) O(1) O(1)
class Solution:
def averageValue(self, nums: List[int]) -> int:
tmp = list()
for num in nums:
if num % 2 == 0 and num % 3 == 0:
tmp.append(num)
return sum(tmp)//len(tmp) if tmp else 0
?
6221. 最流行的视频创作者(灵活运用 defaultdict() 函数和key关键词)
题目链接:6221. 最流行的视频创作者
题目大意:给你两个字符串数组 creators 和 ids ,和一个整数数组 views ,所有数组的长度都是 n 。平台上第 i 个视频者是 creator[i] ,视频分配的 id 是 ids[i] ,且播放量为 views[i] 。
视频创作者的 流行度 是该创作者的 所有 视频的播放量的 总和 。请找出流行度 最高 创作者以及该创作者播放量 最大 的视频的 id 。
- 如果存在多个创作者流行度都最高,则需要找出所有符合条件的创作者。
- 如果某个创作者存在多个播放量最高的视频,则只需要找出字典序最小的 id 。
返回一个二维字符串数组 answer ,其中 answer[i] = [creatori, idi] 表示 creatori 的流行度 最高 且其最流行的视频 id 是 idi ,可以按任何顺序返回该结果。
例如:
输入:creators = ["alice","bob","alice","chris"], ids = ["one","two","three","four"], views = [5,10,5,4]
输出:[["alice","one"],["bob","two"]]
解释:
alice 的流行度是 5 + 5 = 10 。
bob 的流行度是 10 。
chris 的流行度是 4 。
alice 和 bob 是流行度最高的创作者。
bob 播放量最高的视频 id 为 "two" 。
alice 播放量最高的视频 id 是 "one" 和 "three" 。
由于 "one" 的字典序比 "three" 更小,所以结果中返回的 id 是 "one" 。
输入:creators = ["alice","alice","alice"], ids = ["a","b","c"], views = [1,2,2]
输出:[["alice","b"]]
解释:
id 为 "b" 和 "c" 的视频都满足播放量最高的条件。
由于 "b" 的字典序比 "c" 更小,所以结果中返回的 id 是 "b" 。
-
解题思路:灵活运动 defaultdict() 函数 记住括号里面加入数据类型 非常省力!!!另外,key 关键词 太棒了,一定要好好使用。
-
时间复杂度:构造函数复杂度为 O ( N ) O(N) O(N) ,N为creators数组长度
-
空间复杂度:构造函数复杂度为 O ( N ) O(N) O(N)
-
非常好的代码
class Solution:
def mostPopularCreator(self, creators: List[str], ids: List[str], views: List[int]) -> List[List[str]]:
d,c = defaultdict(list),defaultdict(int)
for a,i,v in zip(creators,ids,views):
c[a] += v
d[a].append([i,v])
mx = max(c.values())
ans = list()
for key in c:
if c[key] == mx:
a = d[key]
a.sort(key=lambda x:(-x[1],x[0]))
ans.append([key,a[0][0]])
return ans
- 我的代码 辛辛苦苦 写了一个小时 真实 菜哦。
class Solution:
def mostPopularCreator(self, creators: List[str], ids: List[str], views: List[int]) -> List[List[str]]:
# 我的思路 哎 还是动态规划部分给卡脖子了
# 1) 找最大的 creators 名字集合 为 tmp
# 2) 找每一个 creators 对应的最大自己的名字保存在 h2中
# 3) 遍历 tmp 读出 对应tmp中每个 creator 的 最大子集 保留
h1 = dict()
h2 = dict()
for a,b in zip(creators,ids):
h1[a] = 0
h2[a] = b
# 1) 第一步
for a,c in zip(creators,views):
h1[a] += c
tmp = list()
max_c = max(h1.values())
for a,c in h1.items():
if c==max_c:
tmp.append(a)
# 2)第二步 一定要用心啊!
arr = sorted(zip(creators,ids,views))
i,n = 0,len(arr)
# 排序后的 数组有规律 而后使用双指针锁定检索区间
# 找出 每一个 creator 的最大子集的id
while i<n-1:
c1 = arr[i][0]
j = i+1
while j<n and arr[j][0] == c1:
j += 1
# 这个 t 的应用必须长记性!!! 一会写一篇 blog
t = 0
for k in range(i,j):
d,e = arr[k][1],arr[k][2]
if t==0 or t<e or (t==e and d<h2[c1]):
t = e
h2[c1] = d
i = j
# print(h2)
ans = list()
for f in tmp:
ans.append([f,h2[f]])
return ans
?
6222. 美丽整数的最小增量(map巧用非常好地一个用法 值得学习!)
题目链接:6216. 使数组相等的最小开销
题目大意:给你两个正整数 n 和 target 。
如果某个整数每一位上的数字相加小于或等于 target ,则认为这个整数是一个 美丽整数 。
找出并返回满足 n + x 是 美丽整数 的最小非负整数 x 。生成的输入保证总可以使 n 变成一个美丽整数。
输入:n = 16, target = 6
输出:4
解释:最初,n 是 16 ,且其每一位数字的和是 1 + 6 = 7 。在加 4 之后,n 变为 20 且每一位数字的和变成 2 + 0 = 2 。可以证明无法加上一个小于 4 的非负整数使 n 变成一个美丽整数。
输入:n = 467, target = 6
输出:33
解释:最初,n 是 467 ,且其每一位数字的和是 4 + 6 + 7 = 17 。在加 33 之后,n 变为 500 且每一位数字的和变成 5 + 0 + 0 = 5 。可以证明无法加上一个小于 33 的非负整数使 n 变成一个美丽整数。
输入:n = 1, target = 1
输出:0
解释:最初,n 是 1 ,且其每一位数字的和是 1 ,已经小于等于 target 。
- 解题思路:思路不难 该先做第三题的! 这里面 map() 函数用得太简洁舒服了。
- 时间复杂度: O ( N log ? 2 n ) O(N \log^2 n) O(Nlog2n),n为输入数字
- 空间复杂度: O ( 1 ) O(1) O(1)
class Solution:
def makeIntegerBeautiful(self, n: int, target: int) -> int:
def get_sum(x):
return sum(map(int,str(x)))
def change(x):
y = 1
while x%10 == 0:
y *= 10
x //= 10
x += 10-x%10
return x*y
x = n
while get_sum(x) > target:
x = change(x)
return x-n
?
6223. 移除子树后的二叉树高度(奇偶邻项变化)
题目链接:6223. 移除子树后的二叉树高度
题目大意:给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
- 从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意: - 查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
- 树的高度是从根到树中某个节点的 最长简单路径中的边数 。
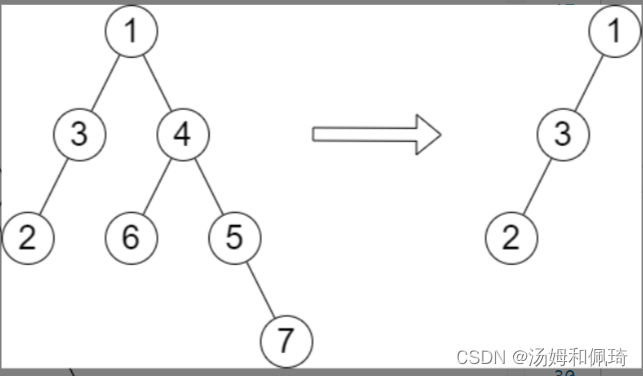
输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出:[2]
解释:上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2(路径为 1 -> 3 -> 2)。
输入:root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出:[3,2,3,2]
解释:执行下述查询:
- 移除以 3 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 4)。
- 移除以 2 为根节点的子树。树的高度变为 2(路径为 5 -> 8 -> 1)。
- 移除以 4 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 6)。
- 移除以 8 为根节点的子树。树的高度变为 2(路径为 5 -> 9 -> 3)。
- 解题思路:3步走
- 由 +1 -1 得知 邻项交换法:大的匹配大的,小的匹配小的
- +2 -2 不会改变数字的奇偶性
- 排序匹配。
- 时间复杂度: O ( N ) O(N) O(N),N为二叉树结点个数
- 空间复杂度: O ( N ) O(N) O(N)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
sh = defaultdict(int)
def check(u,d):
nonlocal sh
if not u: return 0
h = max(check(u.left,d+1),check(u.right,d+1))
h = max(h,d)
sh[u.val] = h
return h
check(root,0)
zr = defaultdict(int)
def dfs(u,h,d):
if not u: return
zr[u.val] = h
h = max(h,d)
h1=h2=h
if u.left:
h2 = max(h,sh[u.left.val])
if u.right:
h1 = max(h,sh[u.right.val])
dfs(u.left,h1,d+1)
dfs(u.right,h2,d+1)
dfs(root,0,0)
ans = []
for q in queries:
ans.append(zr[q])
return ans
总结
?? 努力 奋斗!通过1道,又要掉分了,不过这次还是学到好多有用的东西,继续吧!