开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 二分查找在leetcode部分题中的具体应用 -> 正文阅读

[数据结构与算法]二分查找在leetcode部分题中的具体应用

前言

二分查找之前有过介绍，这是一种十分高效的查找方法。本文将结合一些力扣题介绍二分查找的具体应用。以及在使用二分查找的时候一些需要注意的细节。

1.力扣704. 二分查找

1.题目分析

题目链接直接点击
在这里插入图片描述

这道题没什么好说的直接用二分查找即可。也是二分查找的常规写法和常规应用，之所以拿出来讲，只是为了复习一下二分查找的基本写法。之前的博客中也介绍过二分查找。二分查找就是通过每次缩小区间范围来找到目标值。前提是这个数组是按顺序排列的，要么升序要么降序。

代码示例

int search(int* nums, int numsSize, int target){
    int left=0;
    int right=numsSize-1;
    while(left<=right)
    { int mid=(right-left)/2+left;
      if(nums[mid]>target)
      {
          right=mid-1;
      }
      else if(nums[mid]<target)
      {
          left=mid+1;
      }
      else
      {
          return mid;
      }
    }
 return -1;
}

while循环我是取了等于的，在有些二分查找的代码中while循环有时候取等，有时候不取等。我们先搞清楚取等时是什么情况。所谓取等就是当left和right指向同一个位置时就还要查找一次，才会结束查找。
这道题中取不取等都是没有影响的。为啥呢？查找肯定会有两种情况，无非就是找到了或者没有找到。当数组中存在目标值在查找过程中当left和right还没指向同一个位置之前就会被找到。如果数组中不存在目标值，哪怕left right 指向同一个位置继续查找一次还是不会找到，因为数组中压根没有这个数。所以取不取等都没有影响。我之所以取等是为了说明这个取等条件不影响这道题。

2.力扣剑指 Offer 11. 旋转数组的最小数字

1.题目分析

题目链接直接点击
在这里插入图片描述

这道题解法很多，其中二分查找也能解决这道题。在介绍二分查找之前，先说一下我最开始的暴力解法直接用冒泡排序对数组排了个序，当然你调用语言自带的排序API也行。之后通过观察发现有个有趣的现象。因为这个数组相当于是有序数组右旋k次后得到的一个新数组。也就是说这个数组在以最小元素为分隔的话，在这个最小元素的数组是有序的，在这个最小的元素之前数组都是有序，在这个最小的元素之后数组也是有序的，但是有一中情况例外就是数组相当于没有旋转。这个时候第一个元素就是最小的。

在这里插入图片描述
代码示例

int minArray(int* numbers, int numbersSize){
    
    for(int k=0;k<numbersSize-1;k++)
    {
        if(numbers[k]>numbers[k+1])
        {
            return numbers[k+1];
        }
    }
    return numbers[0];
}

注意一点就是在这个数组旋转某次后相当于没有旋转，这个时候数组就还是升序的，直接返回第一个数组元素即可。

说了这种解法以后该说说二分解法了，我们通过上述所说知道了这个数组是会有临界值的，这个临界值就是最小的元素，我们可以通过二分的方式不断逼近这个临界值即可。当然这个查找方式可能和平时普通二分查找有些许不同。后面会对实现细节详解的。

2.代码示例与总结

代码示例

int minArray(int* numbers, int numbersSize){
   int left= 0;
    int right = numbersSize - 1;
    while (left <= right) 
    {
        int mid = left + (right - left) / 2;
        if (numbers[mid] < numbers[right]) {
            right = mid;
        }
        else if (numbers[mid] > numbers[right]) {
            left = mid + 1;
        }
        else {
            right--;
        }
    }
    return numbers[left];
}

首先这个left right mid写法和循环条件还是不变。这个查找最后的返回值为啥会是left所指向的数呢？首先我们知道在正常的二分查找中left指向最开始最小的元素的，随着遍历除了left和right指向同一个位置时，left始终是指向left和right区间中最小的元素的。这道题就是求整个数组区间最小的元素，也就是相当于反过来求left在正常二分查找中最开始指向的元素。如果nums[mid]中间值小于nums[right]说明这部分还是有序的，right=mid,之所以right没有写成right=mid-1,因为你不能保证这个mid是不是最小的，如果这个mid是最小的，mid-1相当于跳过了这个位置，循环结束这个位置都不会被再次指向。如果nums[mid]>nums[left]，这说明最小的元素在mid在right之间，因为这个时候区间中元素顺序就被改变了，不在是顺序了。这个时候left=mid+1,因为此时的nums[mid]>nums[right]，那么说明nums[mid]肯定不是最小的元素，因此是mid+1。因为这个数组中有重复的元素，所以当中间值等于nums[right]时只用将right--即可所小区间。最后返回left指向的元素即可。
我们可以看到left只有在一种情况下会被改变指向也就是元素顺序发生紊乱不在是顺序的时候。这个很好理解这就说明最小元素在这个区间范围里，通过缩小范围让left指向最小的元素。当区间是顺序时就是不断缩小右区间left指向的左区间不用移动，找到left<right这个条件被打破，left指向的就是最小的元素。这题while循环取不取等都行，因为如果不取等left循环到最后肯定是指向最小元素的位置的，right指向的肯定是left前一个位置，这样跳出循环完全不影响结果的，如果取等了，left和right都指向最小的元素之后才结束循环，left的指向是没有改变的，所以也不影响结果。

3.力扣35. 搜索插入位置

1.题目分析

题目链接直接点击

在这里插入图片描述

这道题也是可以二分来做，但是我最开始没有用二分查找来解决。这个数组是顺序排列的，我们只用遍历数组比较每个元素和target的大小，如果target小于等于某个元素直接返回该元素下标即可。这种做法可以理解为现在有一个从低到高的队列，现在插进来一个人，插进一个人之后，这个队列还是有序的。只需要从头开始挨个比较，如果比某人矮或者和某人一样高直接插进去占据这个人原有的位置即可，不用担心如果比某人矮，前面还有一个人和插进去的人一样高这种情况，这种情况根本不可能出现。队伍是有序的，如果出现了这样的情况，队伍就不是有序的。还有一种情况如果这个人比所有人都要高，直接插入队伍尾部即可。

代码示例

int searchInsert(int* nums, int numsSize, int target){
    for(int i=0;i<numsSize;i++)
    {
        if(target<=nums[i])
        {
            return i;
        }
    }
    return numsSize;
}

注意考虑target比所有的数都要大的情况。

说完了这种方法，我们说一下二分查找。首先left right mid的写法肯定还是一样的。因为数组中可能会出现和target值相同的情况，这个数组是升序的，在这样的情况下就是一个普通的二分查找，所以还是直接返回mid所指向的元素即可。但是如果不存在的话就要好好考虑。

1.第一种情况target大于所有的元素

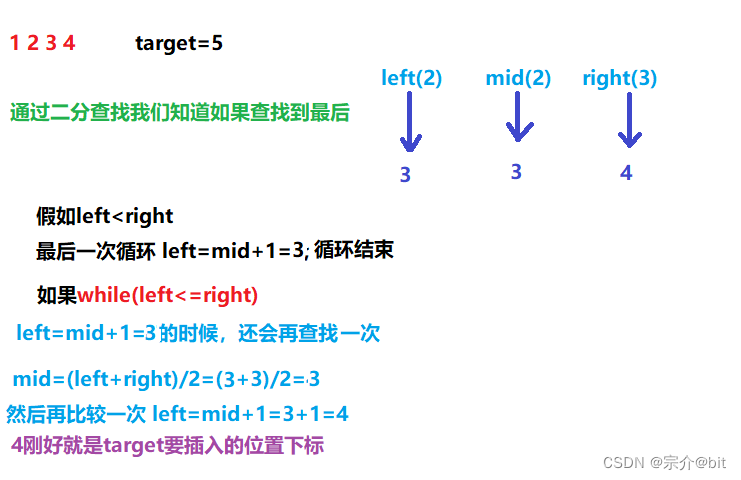
在这里插入图片描述

2.就是在中间插入的情况

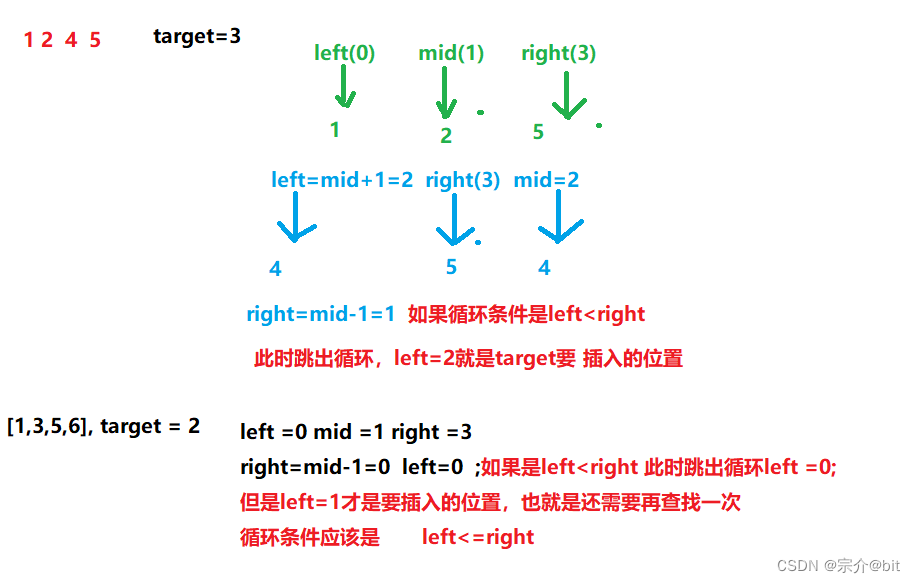
在这里插入图片描述

我们看到有时候while不取等就可以找到正确的位置，但是有时候需要取等才能才会被找到。接下来将会讨论这种情况产生的原因

2.代码示例与总结

nt searchInsert(int* nums, int numsSize, int target){
    int left=0;
    int right=numsSize-1;
    while (left <=right)
    {
        int mid = (right - left)/2+ left;
        if (target < nums[mid]) 
        {
          right = mid - 1;
        } 
        else if(target==nums[mid])
        {
            return mid;
        }
        else
         {
            left = mid + 1;
         }
    }
  return left;
}

从代码种可以看到和平时普通的二分查找写法没啥不同的，只是返回值是left罢了。我们先说说取等的问题的，首先我们知道这个是每次取到中间值的时候是向下取整的，这个时候会因为查找的target的值会有向左或者向右偏移的问题，区间元素是奇数的情况下中间值是很好确定的，但是是偶数的情况就会向下取整确定中间值，也就是可能有时候需要当left right还指向同一个位置的前提下还需要一次查找，目的是让left往右偏移一个单位。但是有时时候区间个数是奇数时，能确定中间值同时刚好要找的位置不用偏移就不用进行下一次查找了，这个时候循环不取等就可以找到正确的位置。
那么如果while循环取等了，会不会对不用取等的情况造成影响呢？实际上是没有影响的，我们想一下之所以取等是为了让left右偏移一次。如果要找的位置在取等之前以及确定了，最后一次查找一定是right左偏移一次，造成left>right的情况跳出循环，这个时候left指向的位置根本是没有变化的，也就不影响最后的结果。
当掌握二分查找的基本写法后，在遇到二分查找的变形题的时候，不确定取等条件可以先画图推演一下。

4.力扣69. x 的平方根

1.题目分析

题目链接直接点击

在这里插入图片描述

这道题是解法很多，二分查找也可以解决。这道题的要求是估算出一个数的平方，如果某个数开平方是小数直接向下区整即可。我们直接在0到x这个区间内一步步找这个目标值，因为是找开平方数所以用mid的平方去比对x即可。如果刚好是开平方数是整数，那就直接可以找到，如果不是就和上面搜索插入那道题的想法是类似的。

2.代码示例与总结

int mySqrt(int x){
 int right=x;
 int left=1;
 if(x==0||x==1)
  {
    return x;
  }
 while(left<=right)
  {
      long long mid=(right-left)/2+left;
      if(mid*mid<x)
       {
           left=mid+1;
       }
       else if(mid*mid==x)
       {
           return (int)mid;
       }
       else
       {
           right=mid-1;
       }
  }
  return left-1;
}

left从0开始lright从x开始，数据范围给的是非负整数所以就从0开始了，这个循环条件取等了，返回值left减1了。这是为啥呢，当循环到最后left和mid是很接近的，如果while不取等就可以找到，那么取等的时候是相当于left偏移了一次，left减去1才是最终答案，当while取等后才能找的数，实际上这个平方数是mid，也就是left和right指向同一个数的时候。当这一步之后left变成了 mid+1,循环结束。在最后一次循环结束时一定是left=mid+1后，left不能被写成left=mid的形式，这会造成死循环，所以就只能left-1了，我们注意到这题如果平方数不等于整数是要向下取整的，而上面搜索位置那道题，当求在数组间插入的位置时实际上是相当于向上取整的，left不用减1.
当理不清循环取等时和最后返回值的情况时，是需要画图梳理。因为结果可能溢出所以mid定义的是长整型。

5.总结

二分查找的精髓就是不断缩小区间进行查找。二分查找写起来并不难，但是实际上有时候遇到的题是二分查找的变种形式，我们需要理清查找过程，什么时候循环要取等，返回值是什么都需要慢慢理清。可以根据给出的示例先画图思考，最后在动手写代码，而不是上来就开始写代码。二分查找没有固定的写法，根据题目要求适当做出变通。

以上内容如有问题，欢迎指正！