LeetCode [977. 有序数组的平方]
题目:给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
-
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100] -
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
思路:
- 暴力解法:先考虑先把数组遍历,遍历后进行平方运算,把平方运算后的数组放进新数组res[],最后再把新数组*res[]*进行冒泡排序,就达到了非递减顺序的要求。
- 暴力优化解法:先考虑先把数组遍历,遍历后进行平方运算,把平方运算后的数组放进新数组res[],最后再把新数组*res[]*通过Arrays.sort()函数进行排序。
- 双指针算法:leftIndex指向起始位置,rightIndex指向终止位置。定义一个新数组res,和原数组一样的大小,让index指向res数组终止位置。
//暴力算法
class Solution {
public int[] sortedSquares(int[] nums) {
int[] res = new int[nums.length];
int temp;
for(int i = 0;i < nums.length;i++){//数组遍历
res[i] = nums[i] * nums[i];//进行平方运算并放进新数组res[]
}
for(int i = 0;i < res.length - 1;i++){//进行冒泡排序
for(int j = 0;j < res.length - 1;j++){
if(res[j] > res[j + 1]){
temp = res[j];
res[j] = res[j + 1];
res[j + 1] = temp;
}
}
}
return res;
}
//暴力优化算法
class Solution {
public int[] sortedSquares(int[] nums) {
int[] res = new int[nums.length];
for(int i = 0;i < nums.length;i++){//数组遍历
res[i] = nums[i] * nums[i];//进行平方运算并放进新数组res[]
}
Arrays.sort(res);
return res;
}
}
//双指针算法
class Solution {
public int[] sortedSquares(int[] nums) {
int rightIndex = nums.length - 1;
int leftIndex = 0;
int[] res = new int[nums.length];
int Index = res.length - 1;
while (leftIndex <= rightIndex) {
if (nums[leftIndex] * nums[leftIndex] > nums[rightIndex] * nums[rightIndex]) {
res[Index--] = nums[leftIndex] * nums[leftIndex];
leftIndex++;
} else {
res[Index--] = nums[rightIndex] * nums[rightIndex];
rightIndex--;
}
}
return res;
}
}
扩展:
- Arrays.sort()
-
Arrays.sort()的作用是对括号中的数组进行排序,时间复杂度O(n*logn),方法返回值为void。
是在原来数组的空间基础上进行升序排序,因此不需要定义一个数组接收它,即不需要返回值。
-
Arrays.sort()重载了四类方法:
sort(T[] a):对指定T型数组按数字升序排序。
sort(T[] a,int formIndex, int toIndex):对指定T型数组的指定范围按数字升序排序。
sort(T[] a, Comparator<? supre T> c): 根据指定比较器产生的顺序对T型数组进行排序。
sort(T[] a, int formIndex, int toIndex, Comparator<? supre T> c): 根据指定比较器产生的顺序对T型数组的指定范围进行排序。 -
sort(T[] a) 的使用
import java.util.Arrays;
import java.util.Comparator;
public class ArraysSort {
public static void main(String[] args) {
int[] a={2,5,4,3,1,8};
Arrays.sort(a);
System.out.println(Arrays.toString(a));
}
}
// 结果[1, 2, 3, 4, 5, 8]
- sort(T[] a,int formIndex, int toIndex) 的使用
import java.util.Arrays;
import java.util.Comparator;
public class ArraysSort {
public static void main(String[] args) {
int[] a={2,5,4,3,1,8};
Arrays.sort(a,2,5);
System.out.println(Arrays.toString(a));
}
}
// 结果
// [2, 5, 1, 3, 4, 8]
- sort(T[] a, Comparator<? supre T> c)的使用
// 按第一维元素比较二维数组
import java.util.Arrays;
import java.util.Comparator;
public class ArraysSort {
public static void main(String[] args) {
int[][] nums=new int[][]{{1,3},{1,2},{4,5},{3,7}};
//方法一
Arrays.sort(nums,new Comparator<int[]>(){
@Override
public int compare(int[] a,int[] b){
if(a[0]==b[0]){ // 不明白为什么要这样写 ,自己的基础有问题,不解
return a[1]-b[1];
}else{
return a[0]-b[0];
}
}
});
for (int[] num : nums) {
System.out.println(Arrays.toString(num));
}
}
}
// 结果
/*
[1, 2]
[1, 3]
[3, 7]
[4, 5]
*/
// 按照第二维元素比较二维数组
import java.util.Arrays;
import java.util.Comparator;
public class ArraysSort {
public static void main(String[] args) {
int[][] nums=new int[][]{{1,3},{1,2},{4,5},{3,7}};
//方法一
Arrays.sort(nums,new Comparator<int[]>(){
@Override
public int compare(int[] a,int[] b){
if(a[1]==b[1]){ //同样不解
return a[0]-b[0];
}else{
return a[1]-b[1];
}
}
});
//方法二
/*Arrays.sort(nums,(a,b)->a[1]-b[1]);*/
for (int[] num : nums) {
System.out.println(Arrays.toString(num));
}
}
}
// 结果
/*
[1, 2]
[1, 3]
[4, 5]
[3, 7]
*/
- sort(T[] a, Comparator<? supre T> c)类对象比较的使用
import java.util.Arrays;
import java.util.Comparator;
class Dog{
int size;
int weight;
public Dog(int s, int w){
size = s;
weight = w;
}
}
class DogSizeComparator implements Comparator<Dog>{
@Override
public int compare(Dog o1, Dog o2) {
return o1.size - o2.size;
}
}
class DogWeightComparator implements Comparator<Dog>{ // **在这里尖括号传入的是对象**
@Override
public int compare(Dog o1, Dog o2) {
return o1.weight - o2.weight;
}
}
public class ArraysSort {
public static void main(String[] args) {
Dog d1 = new Dog(2, 50);
Dog d2 = new Dog(1, 30);
Dog d3 = new Dog(3, 40);
Dog[] dogArray = {d1, d2, d3};
printDogs(dogArray);
Arrays.sort(dogArray, new DogSizeComparator());
printDogs(dogArray);
Arrays.sort(dogArray, new DogWeightComparator());
printDogs(dogArray);
}
public static void printDogs(Dog[] dogs){
for(Dog d: dogs)
System.out.print("size="+d.size + " weight=" + d.weight + " ");
System.out.println();
}
}
// 结果
/*
size=2 weight=50 size=1 weight=30 size=3 weight=40
size=1 weight=30 size=2 weight=50 size=3 weight=40
size=1 weight=30 size=3 weight=40 size=2 weight=50
*/
- 在参数中会出现super,这意味着这类型可以是T或者它的父类型。这就是的该方法可以允许所有子类使用相同的比较器。
import java.util.Arrays;
import java.util.Comparator;
class Animal{
int size;
}
class Dog extends Animal{
public Dog(int s){
size = s;
}
}
class Cat extends Animal{
public Cat(int s){
size = s;
}
}
class AnimalSizeComparator implements Comparator<Animal>{
@Override
public int compare(Animal o1, Animal o2) {
return o1.size - o2.size;
}
}
public class ArraysSort {
public static void main(String[] args) {
Dog d1 = new Dog(2);
Dog d2 = new Dog(1);
Dog d3 = new Dog(3);
Dog[] dogArray = {d1, d2, d3};
printDogs(dogArray);
Arrays.sort(dogArray, new AnimalSizeComparator());
printDogs(dogArray);
System.out.println();
Cat c1 = new Cat(2);
Cat c2 = new Cat(1);
Cat c3 = new Cat(3);
Cat[] catArray = {c1, c2, c3};
printDogs(catArray);
Arrays.sort(catArray, new AnimalSizeComparator());
printDogs(catArray);
}
public static void printDogs(Animal[] animals){
for(Animal a: animals)
System.out.print("size="+a.size + " ");
System.out.println();
}
}
// 结果
/*
size=2 size=1 size=3
size=1 size=2 size=3
size=2 size=1 size=3
size=1 size=2 size=3
*/
LeetCode [209. 长度最小的子数组]
题目:给定一个含有 n 个正整数的数组和一个正整数 target 。
? 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在 符合条件的子数组,返回 0 。
-
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。 -
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1 -
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路:
-
暴力算法:最开始就想遍历一遍,判断符合≥target第一遍连续子数组的和,题目要求的是长度最小的连续子数组,所以需要进行嵌套循环,一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环完成了一个不断搜索区间的过程。
枚举数组nums中的每个下标作为子数组的开始下标,对于每个开始下标 i,需要找到大于或等于 i 的最小下标 j,使得从 nums[i] 到nums[j] 的元素和大于或等于 target,并更新子数组的最小长度。(此时子数组的长度是 j - i + 1)
中间思考过为什么是j - i + 1,比如以示例1为例,当第一个for循环的i = 4,即nums[4] = 4,进入第二个for循环中j = 4到j = 5,得出sum = 7,符合≥target(7),所以此时子数组的是nums[4],nums[5],长度为2,count就是5 - 4 + 1,即j - i + 1。
再把每次得到的最小子数组长度进行存储比较,选择其中最小的进行返回。
一开始写完以后基本用例都可以通过,但是运行的时候显示超出时间限制,经过了解发现是LeetCode改了部分测试用例,所以暴力算法的思路算是对的,但是没办法用于这道题目的解答。
-
滑动窗口:通过暴力算法的启发,可以考虑用一个for循环来完成滑动操作。就和Day01中使用过的双指针类似。
//暴力算法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int count = 0;
int sum = 0;
int res = Integer.MAX_VALUE;//int res = nums.length + 1;也是可行的
for(int i = 0;i < nums.length;i++){
sum = 0;
for(int j = i;j < nums.length;j++){
sum += nums[j];
if(sum >= target){
count = j - i + 1;
res = count > res ? res : count;
break;
}
}
}
return res == Integer.MAX_VALUE ? 0 : res;
}
}
//滑动窗口算法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int startIndex = 0;//定义开始的索引
int count = 0;//定义子数组的长度
int sum = 0;//定义子数组和(窗口值)
int res = Integer.MAX_VALUE;//int res = nums.length + 1;也是可行的
//窗口的结束位置就是遍历数组的指针,也就是for循环里的索引(endIndex)。
for(int endIndex = 0;endIndex < nums.length;endIndex++){
//每一轮迭代,将nums[endIndex]加到sum
sum += nums[endIndex];
//如果当前窗口的值大于target了,更新子数组的最小长度count,将此时的nums[startIndex]从sum中减去,并将startIndex右移(缩小窗口),直到sum < target
while(sum >= target){
count = endIndex - startIndex + 1;
res = count > res ? res : count;
sum = sum - nums[startIndex];
startIndex++;
}
}
return res == Integer.MAX_VALUE ? 0 : res;
}
}
扩展:
-
int res = Integer.MAX_VALUE
就是开始把res赋成整型的最大值。然后下面一般都会有个循环,如果res>某个数字,就把res赋值为这个数字,目的是用来找出所有数字中的最小值。
我的理解,设成一个“大数”,目的是用来找出所有数字中的最小值,而Integer.MAX_VALUE又是整型的最大值,可以覆盖绝大部分考虑不到的情况,如果是nums.length + 1,可能会不保险。同理如果是求所有数字中的最大值的话,就可以设成Integer.MIN_VALUE。
LeetCode [59. 螺旋矩阵 II]
题目:给你一个正整数 n ,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
-
示例 1:
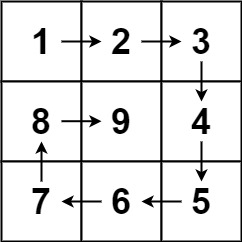
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]] -
示例 2:
输入:n = 1
输出:[[1]]
思路:考虑顺时针的写法,上行的左→右,右列的上→下,下行的右→左,左列的下→上。需要注意的是区间的定义,左闭右开或左开右闭或左闭右闭。可以考虑一种方式,拐角处让给新的一条边来继续画,即左闭右开。
//模拟法
class Solution {
public int[][] generateMatrix(int n) {
int[][] res = new int[n][n];
int left = 0;//从左上开始就是[0,0]起步
int top = 0;//从右上开始就是[0,n - 1]起步
int right = n - 1;//从右下开始就是[n - 1,n - 1]
int buttom = n - 1;//从左下开始就是[n - 1,0]
int num = 1;//后面累加用来判定结束条件,num > sum便结束循环
int sum = n * n;//用来计算矩阵格子的总数
/*
*for循环中变量定义成i或j的细节:按照通常的思维,i代表行,j代表列
*这样,就可以很容易区分出来变化的量应该放在[][]的第一个还是第二个
*对于变量的边界怎么定义:
从左向右:填充的列肯定在[left,right]区间
从上向下:填充的行肯定在[top,bottom]区间
从右向左:填充的列肯定在[right,left]区间
从下向上:填充的行肯定在[bootom,top]区间
*通过上面的总结会发现边界的起始和结束与方向是对应的
*/
while(num <= sum){//解决当n为奇数时,矩阵中心数字无法在迭代过程中被填充的问题
/*
*上侧从左到右
*比如第一轮是从[0(top),0]开始,走到[0(top),n - 1]
*对应的每个格子就内的数字从1开始累加,直到这行走完
*更新边界:从左到右填完后,上边界top++,相当于上边界向内(下)缩1。
*/
for(int j = left;j <= right;j++){
res[top][j] = num++;
}
top++;
/*
*右侧从上到下
*比如第一轮是从[0,n - 1(right)]开始,走到[n - 1,n - 1(right)]
*对应的每个格子内的数字就开始累加,直到这列走完
*更新边界:从上到下填完后,右边界right--,相当于右边界向内(左)缩1。
*/
for(int i = top;i <= buttom ;i++){
res[i][right] = num++;
}
right--;
/*
*下侧从右到左
*比如第一轮是从[n - 1(buttom),n - 1]开始,走到[n - 1(buttom),0]
*对应的每个格子内的数字就开始累加,直到这行走完
*更新边界:从右到左填完后,下边界buttom--,相当于下边界向内(上)缩1。
*/
for(int j = right;j >= left;j--){
res[buttom][j] = num++;
}
buttom--;
/*
*左侧从下到上
*比如第一轮是从[n - 1,0(left)]开始,走到[1,0(left)]
*对应的每个格子内的数字就开始累加,直到这列走完
*更新边界:从下到上填完后,右边界left++,相当于左边界向内(右)缩1。
*/
for(int i = buttom;i >= top;i--){
res[i][left] = num++;
}
left++;
}
return res;
}
}
总结:
- 经过两天的练习,发现即便题目大不相同,但是内在的思想却大同小异。循环不变量(控制每轮遍历的区间);双指针法(一个指针去找符合条件的元素,一个指针在原地等待),用的很频繁。其中的思想还需要多加体会。
- 也许是第二天的中等题难度多了,练习的时间明显远高于第一天,导致日常计划有所打乱。所以在日后的时间规划上需要进行改进。之前刷过一部分题目,刷完了就过了,没有系统的整理过。这次我就主要把个人思路的变化,以及生疏知识的扩招,按照自己习惯的方式进行记录。先用Typora写好,再发到博客上进行记录。坚持就是胜利,努力为春招做好准备。加油!