[数据结构与算法]图【经典算法】-数据结构

# 图论
图论算法可以说是在数据结构中有着极其重要的存在，它的算法都不难理解，主要是如何去存储这个图结构

图结构

通常采用二维数组的方式存储

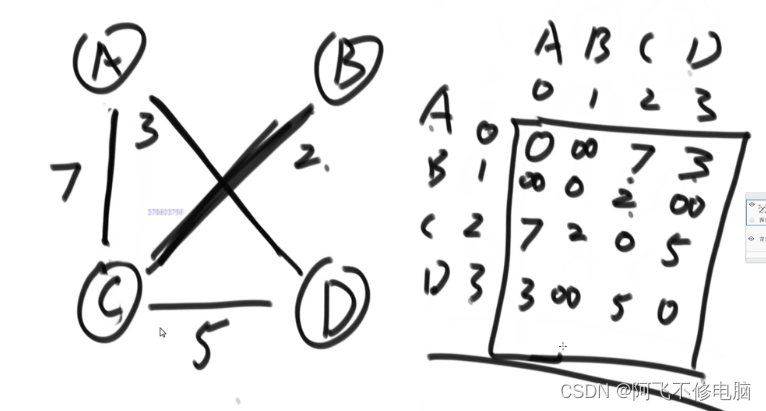
也可以采用一维数组存储

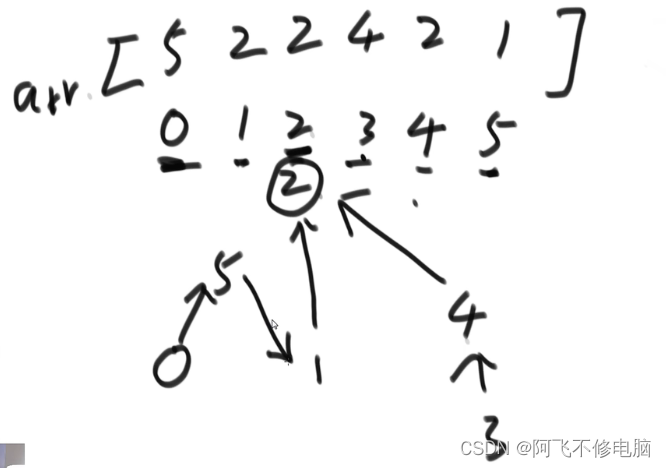
代码表示如下
点集

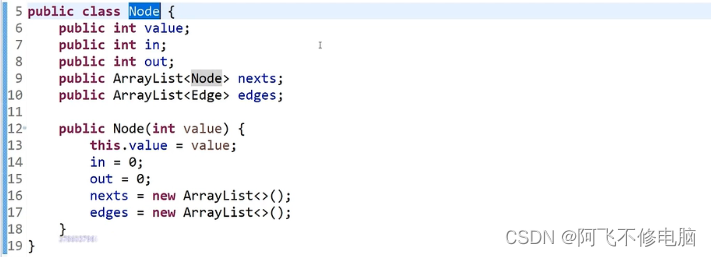
边集

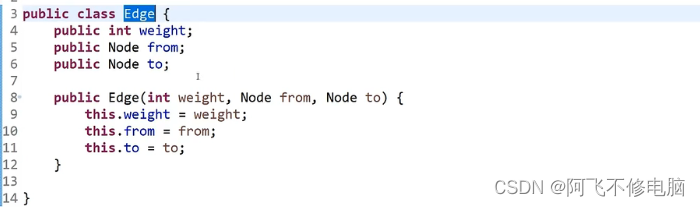
经典算法

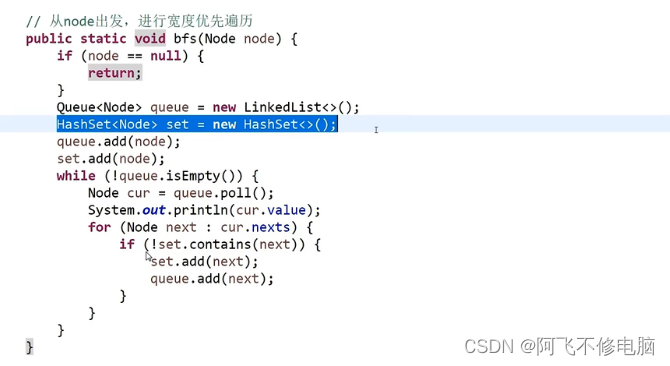
BFS（宽度优先遍历）

BFS也称宽度优先遍历，即一层一层的遍历，相对于DFS（深度优先遍历），用到了队列的结构。宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

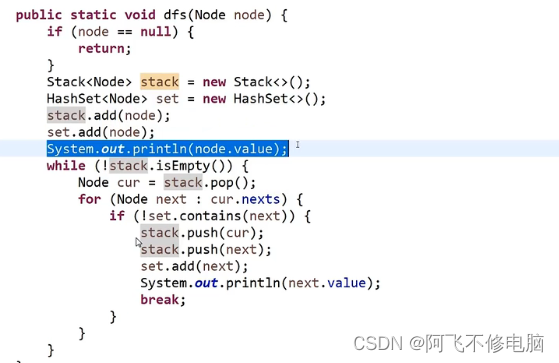
DFS（深度优先便利）

DFS也称深度优先遍历，就是一条路走到黑，遇到能走的就一直走

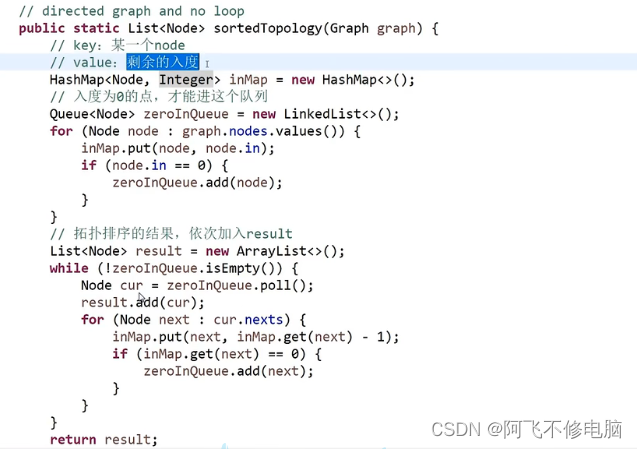
拓扑排序

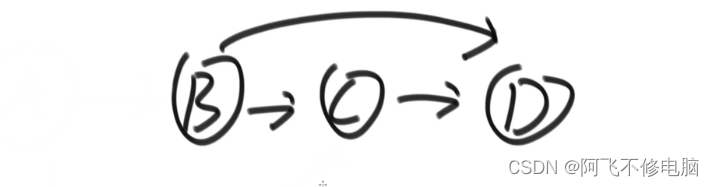
拓扑排序就是每一步都要由上一步作为条件，才能走到下一步，适合用于工程算法

如下图，走到B必须完成A，算法的关键：完成一步，把完成的节点删除掉，并且把和这个节点有关的依赖都删掉，例如：删掉A，把关于A的依赖都删除掉

克鲁斯卡尔算法（Kruskal）

用于最小生成树（就是边权最小的树）的算法，也称K算法（适用于无向图）

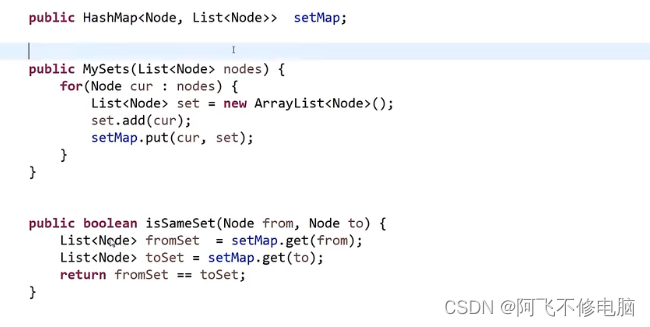
• setMap用于存储一个点的信息，包括该点和该点连接下一节点的集合
• isSameSet用于判断fromSet和toSet是不是来自一个集合，用于判断会不会形成环
• union用于合并from和to
  
  
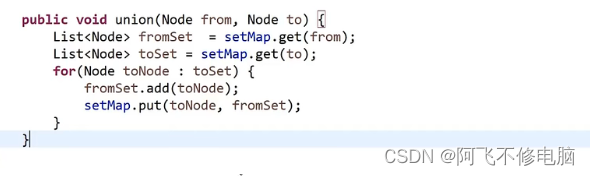
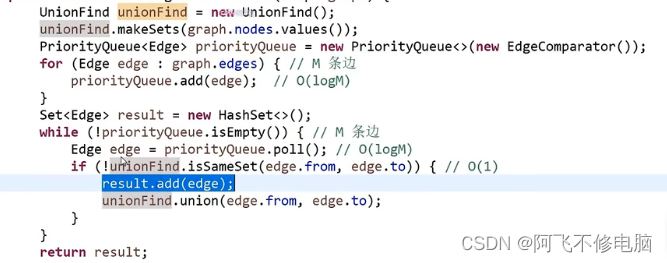
  K算法主函数

//（无向图）k算法：从边角度出发，依次选择最小的边，如果加上这条边会形成环，则不加这条边，如果不会形成环，则加上这条边
//怎么判断会不会形成环，关键在于isSameSet函数，如果在一个集合中就会形成环

public static class MySets{
	//key=节点  value=节点当前所在的集合
	public HashMap<Node, List<Node>> setMap;
	public MySets(List<Node> nodes){
		for(Node cur : nodes){
			List<Node> set = new ArrayList<Node>();
			set.add(cur);
			setMap.put(cur,set);
		}
	}
	//判断两个节点是否在同一个集合
	public boolean isSameSet(Node from,Node to){
		List<Node> fromSet = setMap.get(from);
		List<Node> toSet = setMap.get(to);
		return fromSet == toSet;
	}
	
	//将两个节点加在同一个集合里
	public void union(Node from,Node to){
		List<Node> fromSet = setMap.get(from);
		List<Node> toSet = setMap.get(to);
		//遍历to节点所在集合里的所有元素
		for(Node toNode : toSet){
			//from节点所在的集合加入to节点所在集合的元素
			fromSet.add(toNode);
			//在setmap里更新这些节点当前所在的集合
			setMap.put(toNode,fromSet);
		}
	}
	//比较器
	public static class EdgeComparator implements Comparator<Edge> {
		@Override
		public int compara(Edge o1,Edge o2){
			return o1.weight-o2.weight;
		}
	}
	//k算法
	public static Set<Edge> kruskalMST(Graph graph){
		//将图里的点集放进mysets结果初始化，每个节点就是一个集合
		MySets mysets = new MySets(graph.nodes.values());
		//优先级队列
		PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
		//把图里的边集中所有边放进优先级队列里按weight权值从小到大排序
		for(Edge edge : graph.edges){
			priorityQueue.add(edge);
		}
		Set<Edge> result = new HashSet<>();
		while(!priorityQueue.isEmpty()){
			//队列每次弹出最小边
			Edge edge = priorityQueue.poll();
			//如果边的from和to不在一个集合就：
			if(!mysets.isSameSet(edge.from,edge.to)){
				//结果集里加入这条边
				result.add(edge);
				//将边的to点所在集合里的点放进from点所在的集合里
				mysets.union(edge.from,edge.to);
			}
		}
		return result;
	}
}
			

下面是并查集版本

P算法（Prim算法）

P算法也称Prim算法，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

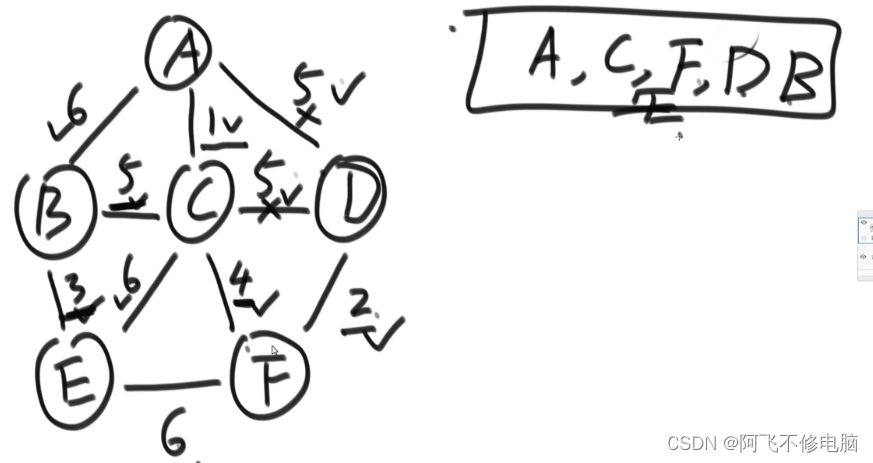
//（无向图）p算法：从一个点出发，从他的边集里解锁边，再从这些边里挑选权值最小的边，然后解锁下一个节点，再从边集里解锁并挑选权值最小的边（包括之前解锁的边），如果边的to点是已经解锁的节点，则不要这条边，然后重复上述过程，最后形成最小生成树

//比较器
public static class EdgeComparator implements Comparator<Edge>{
	@Override
	public int compara(Edge o1,Edge o2){
		return o1.weight-o2.weight;
	}
}
public static Set<Edge> primMST(Graph graph){
	//解锁的所有边都放进小根堆排序
	PriorityQueue<Edge> priortyQueue = new PriorityQueue<>(new
	EdgeComparator());
	//解锁过的点都放进set集里
	HashSet<Node> set = new HashSet<>();
	//选择后的边都放进result里
	Set<Edge> result = new HashSet<>();
	//遍历所有点集是要防止森林的情况，每一次从一个点出发只会形成一棵树
	for(Node node : graph.nodes.values()){
		if(!set.contains(node)）{
			//将解锁了的node放进set里记录
			set.add(node);
			//将node属于的所有边放进优先级队列里排序
			for(Edge edge : node.edges){
				priorityQueue.add(edge);
			}
			while(!priorityQueue.isEmpty()){
				//从优先级队列里弹出最小的边
				Edge edge = priorityQueue.poll();
				//获得node的边的to节点
				Node toNode = edge.to;
				//如果set里没有to节点，则解锁to节点
				if(!set.contains(toNode)){
					//将解锁的to节点放到set里
					set.add(toNode);
					//result集里加入node和to这条最短的边
					result.add(edge);
					//再将to节点解锁的所有边放进优先级队列，继续根据队列里最小的边解锁下一个节点和其边集
					for(Edge nextEdge : toNode.edges){
						priorityQueue.add(nextEdge);
					}
				}
			}
		}
		return result;
	}

Dijkstra算法

如下图，选A作为出发点，除了A到A距离是0，别的点都设为无穷大，然后找到与A相连的其余节点，根据权重来更新距离，之后选择一个权重最小的边，把A标记上并且封锁，如下图我们可以找到B是权重较小的一个节点，下一次从B开始，循环往复，直到全部的点都封锁

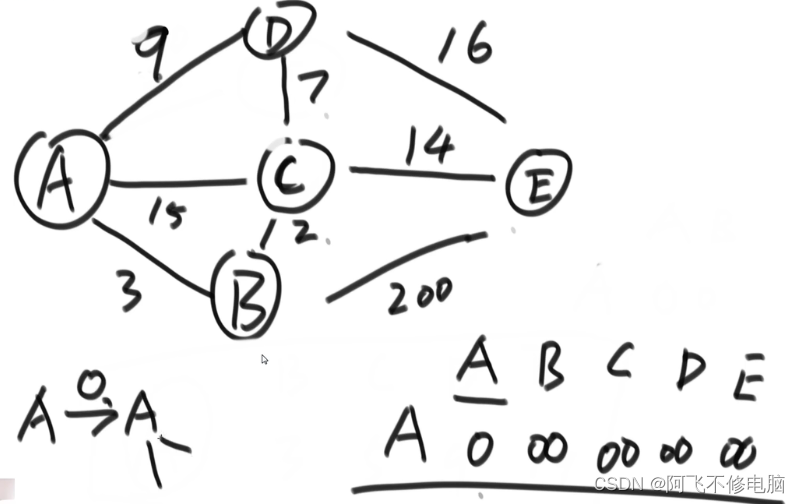
//求从出发节点到其他节点的最短路径
//适用范围：没有累加和为负数的环

public static HashMap<Node,Integer> dijkstra(Node node){
	//hashmap表记录从head出发到所有点的最小距离
	//key:从head出发到达的点   value:从head出发到达key的最小距离
	//如果在hashmap中，没有T的记录，含义是从head到T这个点的距离为∞
	HashMap<Node, Integer> distanceMap = new HashMap<>();
	distanceMap.put(head,0);
	//已经锁住，确定求得最短距离的节点，存在selectedNodes里
	HashSet<Node> selectedNodes = new HashSet<>();
	//从distanceMap里找没有被锁住并且离head最小距离的节点记录
	Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedMap);
	While(minNode != null){
		//先拿到head到minNode的距离
		int distance = distanceMap.get(minNode);
		//遍历minNode的边集
		for(Edge edge : minNode.edges){
			//拿到minNode的边的to点
			Node toNode = edge.to;
			//如果toNode是没有锁住的点
			if(!distanceMap.containskey(toNode)){
				//在distanceMap里更新to点的信息，距离为head到minNode的距离加上边的weight权值
				distanceMap.put(toNode, distance +  edge.weight);
			}
			//如果toNode是已经锁住的点，比较原来的distance和加上权值后的distance，选更小的那个
			distanceMap.put(edge.to, Math.min(distanceMap.get(toNode)， distance + edge.weight));
		}
		//更新完minNode的所有路径距离后，将minNode锁住
		selectedNodes.add(minNode);
		//继续从distanceMap里找一个没有被锁住并且离head最小距离的节点来继续遍历
		minNode = getMinDistanceAndUnseletedNode(distanceMap,selectedNodes);
	}
	return distanceMap;				
}

//从距离记录表中寻找一条从head到T的最短距离，且T点是还没有被锁住的，返回T
public static Node getMinDistanceAndUnselectedNode(HashMap<Node,Integer> distanceMap, HashSet<Node> touchedNodes){
	//最短距离的节点
	Node minNode = null;
	//最短距离
	int minDistance = Integer.MAx_VALUE;
	//遍历距离记录表
	for(Entry<Node, Integer> : distanceMap.entrySet()){
		//得到每个节点和其当前到head的最短距离
		Node node = entry.getKey();
		int distance = entry.getValue();
		//如果节点还没被锁并且新解锁边的距离小于minDistance
		if(!touchedNodes.contains(node) && disatance < minDistance){
			//更新最小节点和最小距离
			minNode = node;
			minDistance = distance;
		}
	}
	return minNode;
}	

结语

对以上算法有问题的朋友欢迎在评论区发言，觉得不错还请各位点赞支持