继续学习排序,本篇学习交换排序和归并排序
其中在交换排序中,快速排序是需要掌握的重点

目录
快排大纲一览

一、交换排序
1.冒泡排序
冒泡排序之前学习过链接如下
C语言中常用的数组排序方法:冒泡排序、选择排序、插入排序、数组的移动(含代码详解)以及相关联系题
2.快速排序(效率最高)
所有排序算法中面试官让写概率最高的
| 左侧小于基准值 | 基准值 | 右侧大于基准值 |
两侧数据不一定有序
void QuickSort(int array[], int left, int right)
{
if (right - left <= 16) //这样原因见5
{
return;
}
else
{
// 1. 在[left, right)的区间中找一个基准值,然后按照基准值
// 将区间分割成两部分
int div = Partion(array, left, right);
// div表示分割完成之后基准值在数组中的下标
// 2. 递归排基准值的左侧
QuickSort(array, left, div);
// 3. 递归排基准值的右侧,+!是应为左闭右开
QuickSort(array, div + 1, right);
}
}基准值的选择:基准值取区间中的任意数据都可以,但是为了实现简单,一般取左右两侧的数据作为基准值
对于快排,如何划定基准值区间是十分重要的,主要有三种
2.1?hoare版本
| 3 | 1 | 8 | 6 | 0 | 2 | 7 | 9 | 4 | 5 |
基准值 key = 5
将begin指向3 , end指向5

?第一次走一遍abc结果如下,8与4交换
| 3 | 1 | 4 | 6 | 0 | 2 | 7 | 9 | 8 | 5 |
第二次走abc ,6与2交换
| 3 | 1 | 4 | 2 | 0 | 6 | 7 | 9 | 8 | 5 |
此时继续a,begin与end相遇,循环结束
循环结束之后,将begin位置上的元素与区间最右侧的元素进行交换,6与5交换
| 3 | 1 | 4 | 2 | 0 | 5 | 7 | 9 | 8 | 6 |
此时找到了基准值,达到了目的。左侧小于基准值,右侧大于基准值
最后返回begin或者end即可
// 划分方式一:hoare
// 时间复杂度:O(N)
int Partion1(int array[], int left, int right)
{
int keyIndex = GetMiddleIndex(array, left, right);
Swap(&array[keyIndex], &array[right - 1]);
int begin = left; // 注意begin一定不能从0开始
int end = right - 1;
int key = array[end];
while (begin < end)
{
// 让begin从前往后找,找比基准值大的元素
while (begin < end && array[begin] <= key)
begin++;
// 让end从后往前找,找比基准值小的元素
while (begin < end && array[end] >= key)
end--;
if (begin < end)
{
Swap(&array[begin], &array[end]);
}
}
if (begin != right - 1)
{
// Swap(&array[begin], &key); // 错误
Swap(&array[begin], &array[right - 1]);
}
return begin;
}2.2 挖坑法
| 3 | 1 | 8 | 6 | 0 | 2 | 7 | 9 | 4 | 5 |
基准值 key = 5,将begin指向3 , end指向5

?时间复杂度:O(N)
// 挖坑法
// 时间复杂度:O(N)
int Partion2(int array[], int left, int right)
{
int keyIndex = GetMiddleIndex(array, left, right);
Swap(&array[keyIndex], &array[right - 1]);
int begin = left; // 注意begin一定不能从0开始
int end = right - 1;
int key = array[end]; // end位置现在就是一个坑
while (begin < end)
{
// 让begin从前往后找,找比基准值大的元素
while (begin < end && array[begin] <= key)
begin++;
// 找到比基准值大的元素
if (begin < end)
{
array[end] = array[begin];
end--;
}
// begin位置又是一个新的坑位
// 让end从后往前找比基准值小的元素,去填begin位置的坑
while (begin < end && array[end] >= key)
end--;
if (begin < end)
{
// 去填begin位置的坑
array[begin] = array[end];
begin++;
}
// end位置又是一个新的坑位
}
// 最后需要用key将最后的一个坑位填充
array[begin] = key;
return begin;
}2.3 前后指针法
时间复杂度:O(N)
// 前后指针
// 时间复杂度:O(N)
int Partion(int array[], int left, int right)
{
int cur = left;
int prev = cur - 1;
int keyIndex = GetMiddleIndex(array, left, right);
Swap(&array[keyIndex], &array[right - 1]);
int key = array[right - 1];
while (cur < right)
{
// 让cur从前往后找,找比基准值小的元素
// 找到之后,如果prev的下一个位置和cur不相等则交换
if (array[cur] < key && ++prev != cur)
{
Swap(&array[prev], &array[cur]);
}
++cur;
}
if (++prev != right-1)
{
Swap(&array[prev], &array[right - 1]);
}
return prev;
}当prev和cur 是一前一后关系时,说明cur从前往后找的过程中暂未遇到比基准值大的值
当prev和cur之间有间隔时,prev下一个位置到cur之间的元素都是比基准值大的元素
3.使用场景
快排最差情况
元素基本有序的情况下,在取基准值的时候,每次拿到基准值概率更高,所以:
快排实际上不适合元素基本有序的场景,比较适合元素杂乱的场景
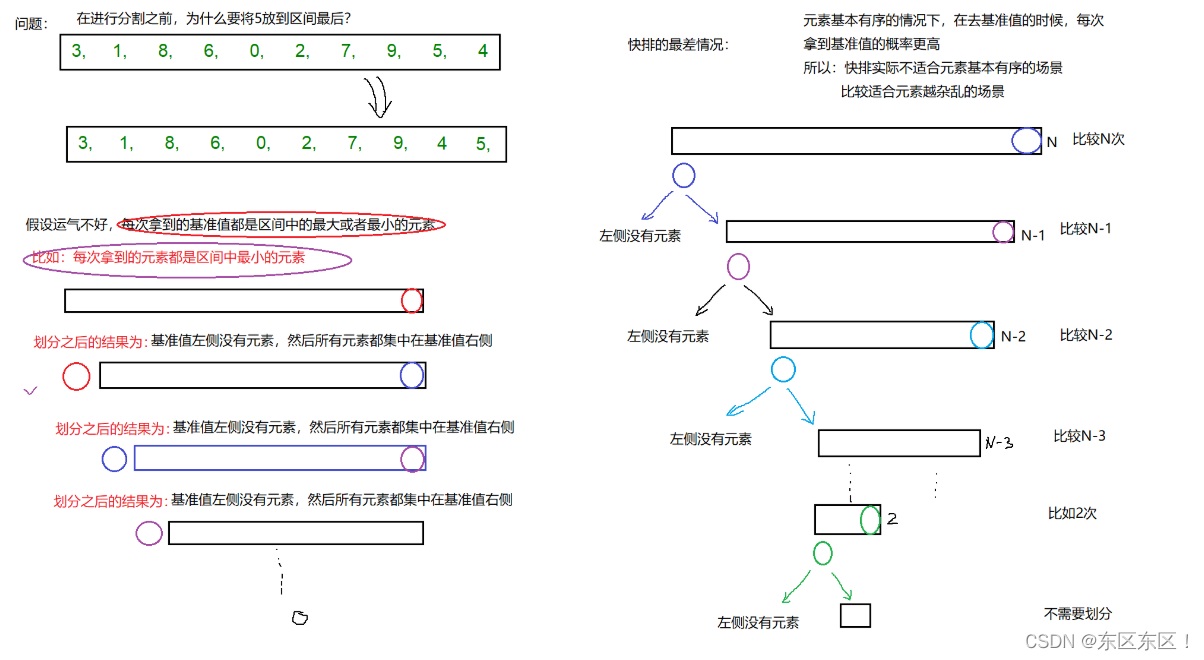
?拿二叉树来说就像一个单支二叉树,每层只有一个节点
最终比较实际复杂度为 O(N^2)
快排最优情况
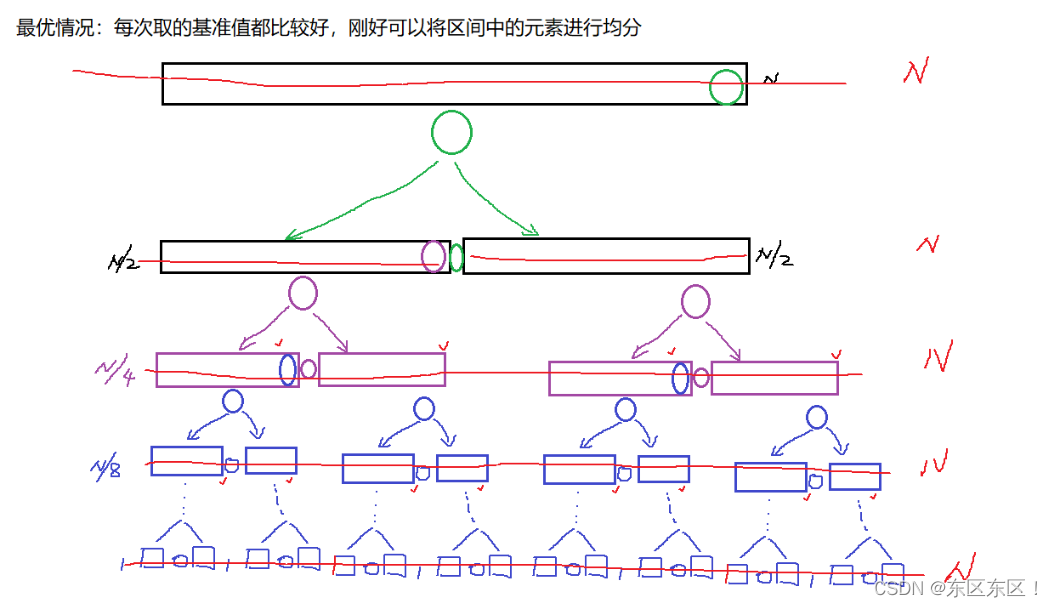
此时二叉树就是一个 二叉平衡树:求高度方式为 logN
最优情况下 时间复杂度 O(NlogN)
4.三数取中优化快排(前面取基准值方法均使用)
为了解决上述快排的问题,采用 三数取中的方法来优化快速排序

/三数取中法优化快排: 主要是降低拿到极值的概率?
int GetMiddleIndex(int array[], int left, int right)
{
int mid = left + ((right - left) >> 1);
// array[left]
// array[mid]
// array[right-1]
if (array[left] < array[right - 1])
{
if (array[mid] < array[left])
return left;
else if (array[mid] > array[right - 1])
return right - 1;
else
return mid;
}
else
{
// array[left] >= array[right-1]
if (array[mid] > array[left])
return left;
else if (array[mid] < array[right - 1])
return right - 1;
else
return mid;
}
}5.再次细分优化
5.1设置阈值
随着递归不断进行,区间元素也越来越少,少于一定数量的时候就不需要往下划分了,不断划分也会增加递归深度,如果本身元素特别多,划分太深会导致栈溢出
所以设置递归的时候不需要区间元素个数少于1的时候递归退出,可以设置一个阈值:当区间元素少于阈值时,可以采用插入排序来对区间中的元素进行排序

?所以就有了本章最开始的代码
void QuickSort(int array[], int left, int right)
{
if (right - left <= 16)
{
return;
}
else
{
// 1. 在[left, right)的区间中找一个基准值,然后按照基准值
// 将区间分割成两部分
int div = Partion(array, left, right);
// div表示分割完成之后基准值在数组中的下标
// 2. 递归排基准值的左侧
QuickSort(array, left, div);
// 3. 递归排基准值的右侧,+!是应为左闭右开
QuickSort(array, div + 1, right);
}
}
5.2 加入堆排序
如果数据量太大,没达到阈值前就已经递归深度过深造成栈溢出
1.设置快排递归次数的阈值,达到这个递归次数就不能继续递归
2.为了不影响快排时间复杂度,后续分组直接采用堆排序处理(选择堆排序的原因是他的时间复杂度也是 O(NlogN))

递归深度:logN 即二叉平衡树高度
6.循环快排
循环快排需要用到栈,记得调用栈的文件
创建栈之后,先把左右边界压入栈中,通过划分基准值,不断递归
void QuickSortNor(int array[], int size)
{
Stack s;
StackInit(&s);
StackPush(&s, size);//压右边界
StackPush(&s, 0); //压左边届
while (!StackEmpty(&s))
{
int left = StackTop(&s);
StackPop(&s);
int right = StackTop(&s);
StackPop(&s);
// [left, right)中的区间进行划分
if (right - left <= 1)
continue;
int div = Partion(array, left, right);
// 基准值的左侧[left, div)
// 基准值的右侧[div+1,right)
// 将基准值的右侧压栈
// 先压右侧然后再压区间的左侧
StackPush(&s, right);
StackPush(&s, div + 1);
// 将基准值的左侧压栈
// 先压右侧然后再压区间的左侧
StackPush(&s, div);
StackPush(&s, left);
}
StackDestroy(&s);
}