文章目录
977. 有序数组的平方
题目:
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums已按 非递减顺序 排序
进阶:
- 请你设计时间复杂度为
O(n)的算法解决本问题
题解
c++代码实现
// 暴力解决
vector<int> sortedSquares(vector<int>& nums) {
for (int i = 0; i< nums.size(); i++) {
nums[i] *= nums[i];
}
sort(nums.begin(), nums.end());
return nums;
}
// 双指针写法
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
int res = nums.size() - 1;
vector<int> result(nums.size(), 0);
// 往后赋值。
for (int i = nums.size() - 1; i >= 0; i--) {
if (nums[left] * nums[left] < nums[right] * nums[right]) {
result[i] = nums[right] * nums[right--];
}else{
result[i] = nums[left] * nums[left++];
}
}
return result;
}
};
python代码实现
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
left = 0
res = right = len(nums) - 1
results = [0] * len(nums)
while res >= 0:
if (nums[left] * nums[left] < nums[right] * nums[right]):
results[res] = nums[right] * nums[right]
right -= 1
else:
results[res] = nums[left] * nums[left]
left += 1
res -= 1
return results
209. 长度最小的子数组
题目:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例2:
输入:target = 4, nums = [1,4,4]
输出:1
示例3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
题解:
这里使用代码随想录动态题解,滑动窗口法
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-o5HTqfwy-1666890994128)(./img/209.长度最小的子数组.gif)]
c++代码实现
// 暴力解法, 会超出时间限制。
//int minSubArrayLen(int target, vector<int>& nums) {
// int result = INT_MAX;
// int n = nums.size();
// int sums = 0;
// for (int i = 0; i < n; i++) {
// sums = 0;
// for (int j = i; j < n; j++) {
// sums += nums[j];
// if (sums >= target){
// result = min(result, j - i + 1);
// break;
// }
// }
// }
// return result == INT_MAX ? 0 : result;
//}
// 滑动窗口
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int start = 0, end = 0, sums = 0;
int result = nums.size() + 1; // 最长长度。
int n = nums.size() - 1;
while (end <= n) {
sums += nums[end++];
// 因为要找长度最小,所以只要大于target,就移动start。找最小。
while (sums >= target) {
// 上面已end++, 所以这里不必 end - start + 1
result = min(result, end - start);
// 移动start,对应和要减去
sums -= nums[start++];
}
}
return (result == (nums.size() + 1)) ? 0 : result;
}
};
python 代码实现
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
start = 0
result = len(nums) + 1
sums = 0
for end in range(len(nums) ):
sums += nums[end]
while sums >= target:
result = min(result, end - start + 1)
sums -= nums[start]
start += 1
if result == (len(nums) + 1):
return 0
else:
return result
59. 螺旋矩阵 II
题目:
给你一个正整数 n ,生成一个包含 1 到
n
2
n^{2}
n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
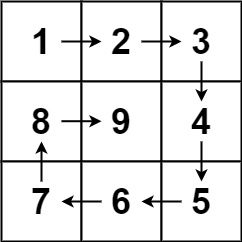
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
题解:
- 按照顺时针遍历
- 从左到右遍历,right尾,左上角已赋值,右上角赋值
- 从上到下遍历,右下角赋值。
- 从右到左, 左下角赋值
- 从底到上。
c++ 代码实现
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int left = 0, right = n -1;
int top = 0, bottom = n - 1;
vector<vector<int>> matrix(n, vector<int>(n));
int num = 1;
// 顺时针遍历
while (left <= right && top <= bottom) {
// 从左到右遍历,right尾,左上角已赋值
for (int col = left; col <= right; col++) {
// top 不会变, 移动col,直到右上角赋值
matrix[top][col] = num++;
}
// 从上到下遍历,bottom收尾
for (int row = top + 1; row <= bottom; row++) {
// right尾不变,移动row,直到右下角赋值。
matrix[row][right] = num++;
}
// 到底层,判断是否已结束
if (left < right && top < bottom) {
// 从右到左,因为右下角已赋值。right - 1遍历
for (int col = right - 1; col >= left; col--){
// bottom 不变,移动col,直到左下角赋值
matrix[bottom][col] = num++;
}
// 从底到上,左下角已赋值,bottom - 1, 上面从左到右第一个左上角已赋值,这里不用 row>=top
for (int row = bottom - 1; row > top; row--) {
// row 不变,left移动
matrix[row][left] = num++;
}
}
// left 加,right 减
// top 加, bottom 减
left ++;
right --;
top ++;
bottom --;
}
return matrix;
}
};
python 代码实现
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix = [[0] * n for _ in range(n)]
num = 1
left, right, top, bottom = 0, n - 1, 0, n - 1
while left <= right and top <= bottom:
for col in range(left, right + 1):
matrix[top][col] = num
num += 1
for row in range(top + 1, bottom + 1):
matrix[row][right] = num
num += 1
if left < right and top < bottom:
for col in range(right - 1, left, -1):
matrix[bottom][col] = num
num += 1
for row in range(bottom, top, -1):
matrix[row][left] = num
num += 1
left += 1
right -= 1
top += 1
bottom -= 1
return matrix