知识导航
一.快速排序
快速排序是1960年由查尔斯·安东尼·理查德·霍尔(Charles Antony Richard Hoare)，一般称为东尼·霍尔（Tony Hoare）。接下来让我们走进这个“很快”
的排序吧！
🥳🥳快速排序，顾名思义是实践中一种快速的排序算法，再c++和java基本类型中都特别有用。他的平均运行时间是O(NlogN),该算法之所以这么快，主要是由于非常精炼和高度优化的内部循环，它的最坏情况是O(n2),但经过稍许努力可以使这种情况极难实现。
也正是因为快速排序的高精度也使算法如果稍有问题就会产生很糟糕的情况。
1.快速排序的原理
快速排序的执行过程:
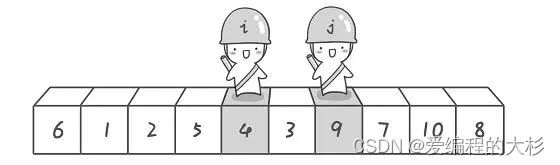
（1） 从序列中选择一个轴点元素（pivot）
? 假设每次选择 0 位置的元素为轴点元素
（2） 利用 pivot 将序列分割成 2 个子序列
? 将小于 pivot 的元素放在pivot前面（左侧）
? 将大于 pivot 的元素放在pivot后面（右侧）
? 等于pivot的元素放哪边都可以
（3） 对子序列进行 （1） （2） 操作
? 直到不能再分割（子序列中只剩下1个元素）
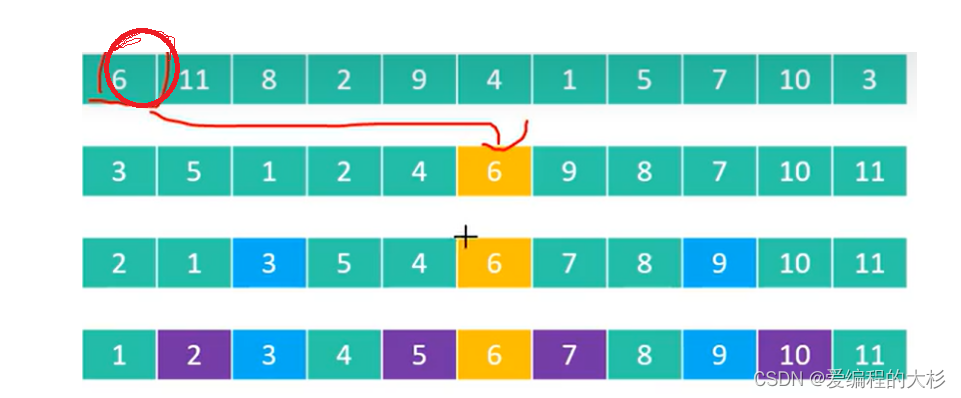快速排序的本质：逐渐将每一个元素都转换成轴点元素
2.轴点构造与代码实现
（1）已知轴点的快排实现
假设我们先以第一个元素作为轴点进行构造
- 将第一个元素进行缓存
2.（1） 数组从右向左进行遍历，如果end位置的数据比缓存的轴点元素（pivot）数大，则直接进行end–，因为右边 本来就是存储比轴点元素大的元素。
（2）如果如果end位置的数据比缓存的轴点元素（pivot）数小或者等于，则将目前的元素覆盖到前面的位置。begin++.并且交换遍历方向。
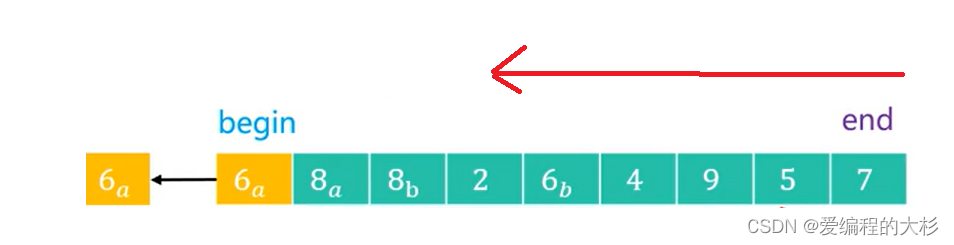
- 重复执行以上1，2过程，得出结果，最后将缓存的轴点元素归位
注意：图中黑色节点代表可以覆盖的空闲节点
代码实现：
public class QuickSort <E extends Comparable<E>> extends Sort<E> {
@Override
public void sort() {
sort(0, array.length);
}
/**
* 对 [begin, end) 范围的元素进行快速排序
* @param begin
* @param end
*/
private void sort(int begin, int end) {
if (end - begin < 2) return;
// 确定轴点位置 O(n)
int mid = pivotIndex(begin, end);
// 对子序列进行快速排序
//这里的begin不要写成0
sort(begin, mid);
sort(mid + 1, end);
}
/**
* 构造出 [begin, end) 范围的轴点元素
* @return 轴点元素的最终位置
*/
private int pivotIndex(int begin, int end) {
// 备份begin位置的元素
//这里的begin不要写成0
E pivot = array[begin];
// end指向最后一个元素
end--;
while (begin < end) {
while (begin < end) {
if (com(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
end--;
} else { // 右边元素 <= 轴点元素
array[begin++] = array[end];
break;
}
}
while (begin < end) {
if (com(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
begin++;
} else { // 左边元素 >= 轴点元素
array[end--] = array[begin];
break;
}
}
}
// 将轴点元素放入最终的位置
array[begin] = pivot;
// 返回轴点元素的位置
return begin;
}
}
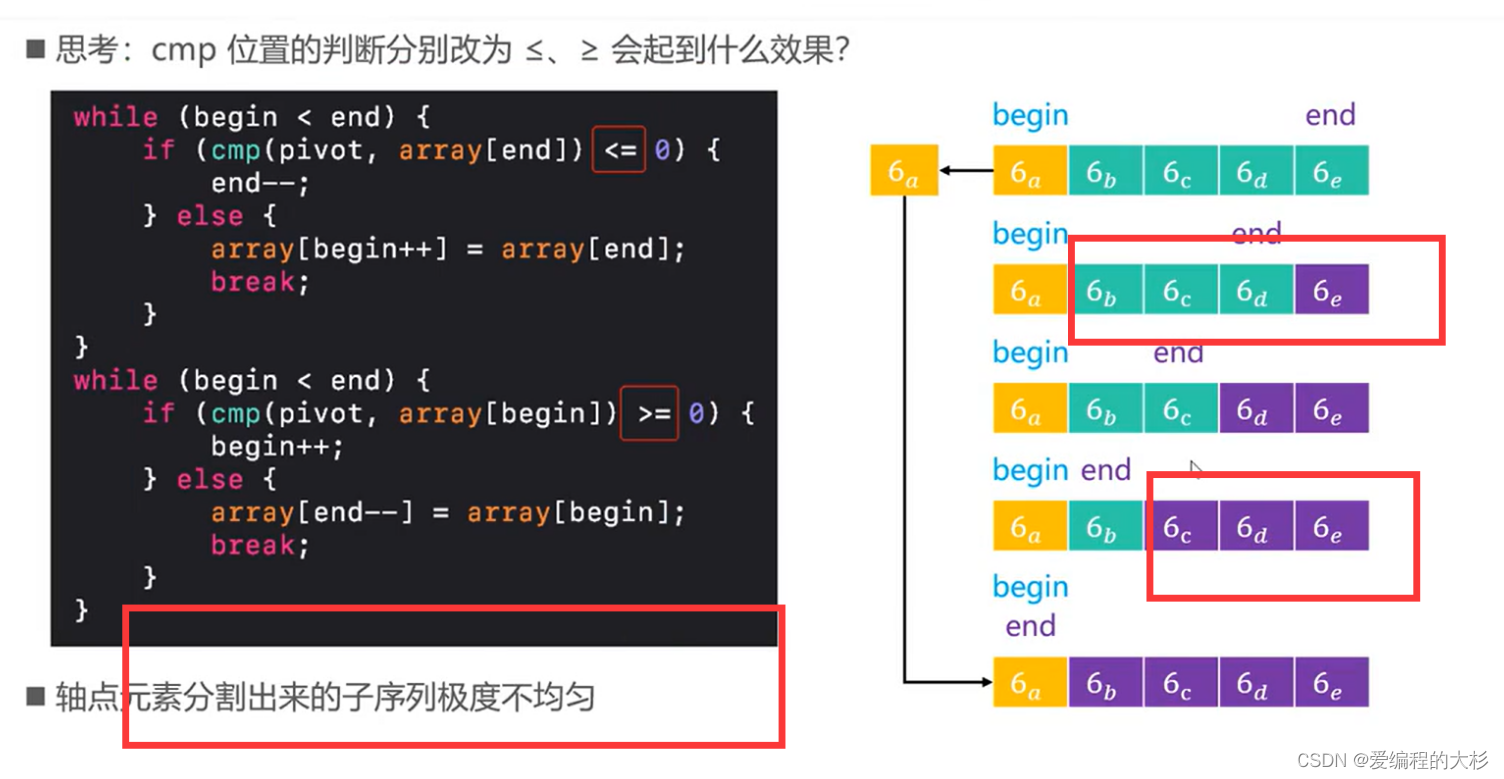
（2）轴点构造的错误用法
上面的流程我们默认轴点为第一个元素，但是这种设计显然不能发挥出快速排序的优点甚至不能看出它比归并排序到底强到哪里。
轴点构造的错误方法
- 将第一个元素作为轴点元素
如果默认将第一个元素作为轴点元素，如果输入数组元素是随机的那是可以接受的，如果输入数组是预排序的或者是反序的，那么就会产生一个恶劣的分割，因为所有点的元素会被统一规划到一边。 - 选取两个互异中的较大者作为轴点元素
这种方法和第一种方法具有同样的危害性
（3）轴点随机化
解决上面的的问题我们就要对上面的轴点的选取进行随机化
我们将begin + (int)(Math.random() * (end - begin)作为轴点元素
Math.random() * (end - begin)的范围是[0，begin-end);
所以begin + (int)(Math.random() * (end - begin)的范围就是[begin,end)
我们只需将上面的代码进行简要改动就能实现轴点元素随机化
🌎 我们只需只需执行这个操作swap(begin, begin + (int)(Math.random() * (end - begin)));将随机生成的轴点元素放在第一个元素的位置就行了
private int pivotIndex(int begin, int end) {
// 随机选择一个元素跟begin位置进行交换
swap(begin, begin + (int)(Math.random() * (end - begin)));
// 备份begin位置的元素
//这里的begin不要写成0
E pivot = array[begin];
// end指向最后一个元素
end--;
while (begin < end) {
while (begin < end) {
if (com(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
end--;
} else { // 右边元素 <= 轴点元素
array[begin++] = array[end];
break;
}
}
while (begin < end) {
if (com(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
begin++;
} else { // 左边元素 >= 轴点元素
array[end--] = array[begin];
break;
}
}
}
5.细节剖析与复杂度分析
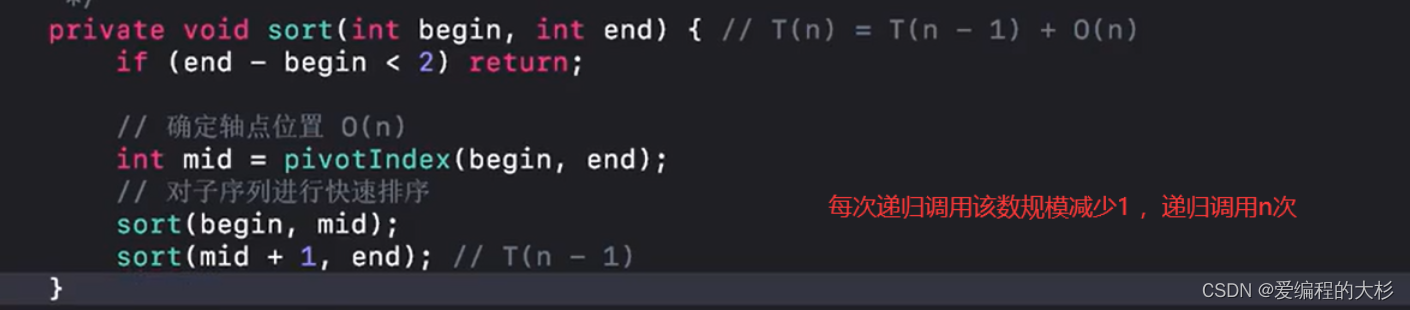
快速排序的核心调用代码：
- 在轴点左右元素数量比较均匀的情况下，同时也是最好的情况
private void sort(int begin, int end) {
if (end - begin < 2) return;
// 确定轴点位置 O(n),需要遍历所有元素
int mid = pivotIndex(begin, end);
// 对子序列进行快速排序
//这里的begin不要写成0
sort(begin, mid);//O(n/2)
sort(mid + 1, end);//O(n/2)
}
所以快速排序的所用到的时间近似为2O(T/2)+O(n),对比递推式表得知最好的情况是O(nlogn)
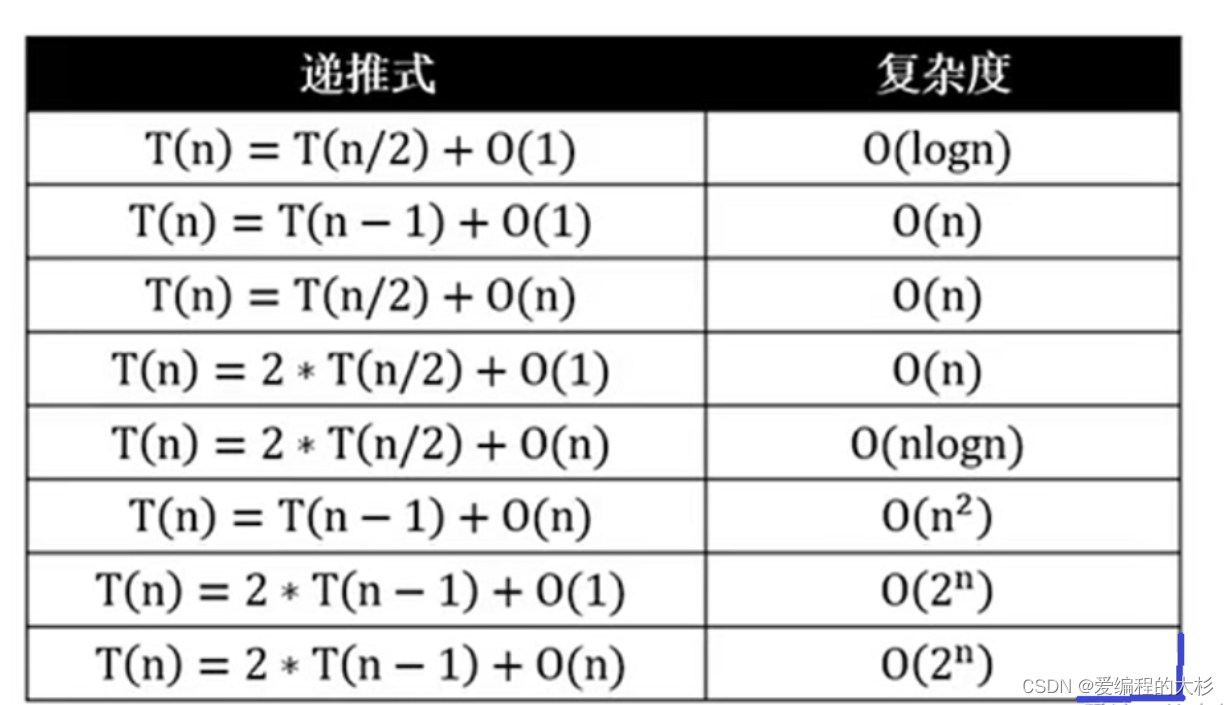
- 如果轴点左右元素数量极度不均匀，最坏情况
T（n）=T(n-1)+O(n)=O(n2) 注：T(n-1)就是一种非常不均匀的情况，每一次数据都被分到一边，则需要分n-1次。
二.希尔排序
1.希尔排序的原理
🤑 1959年由唐纳德·希尔（Donald Shell）提出
👏希尔排序把序列看作是一个矩阵，分成 𝑛 列，逐列进行排序
?𝑛 从某个整数逐渐减为1
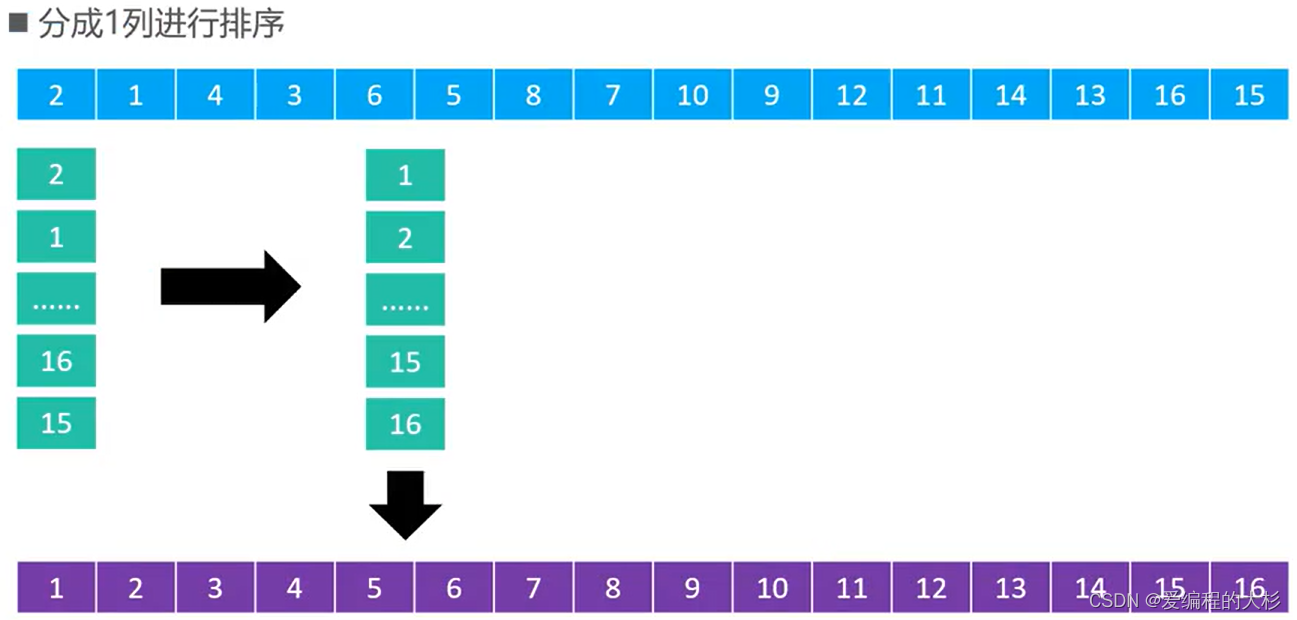
?当 𝑛 为1时，整个序列将完全有序
? 因此，希尔排序也被称为递减增量排序（Diminishing Increment Sort）
? 矩阵的列数取决于步长序列（step sequence）
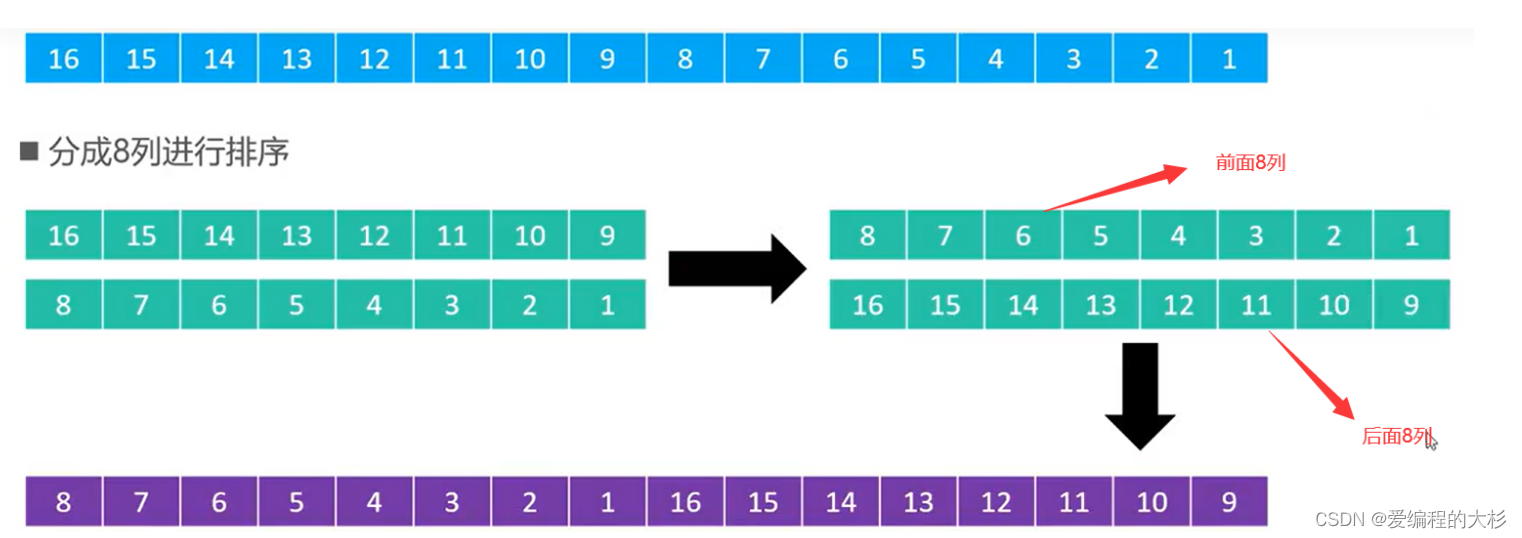
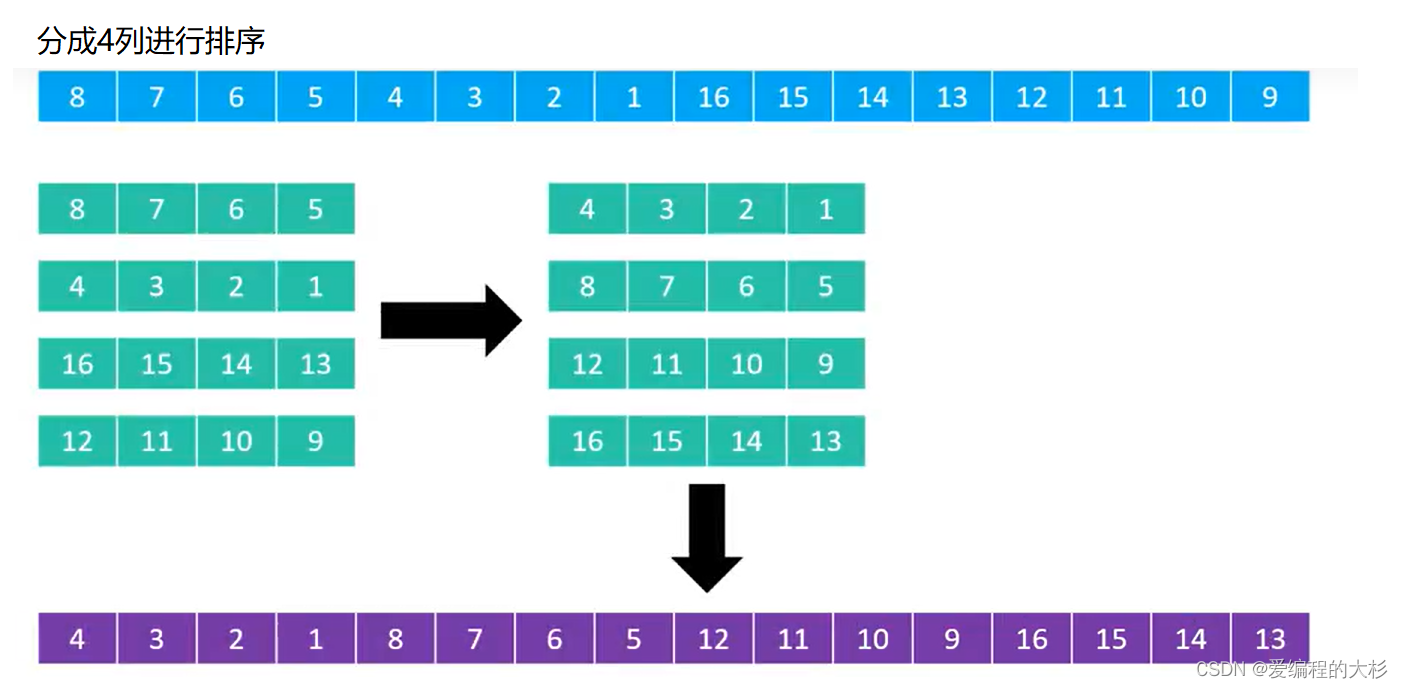
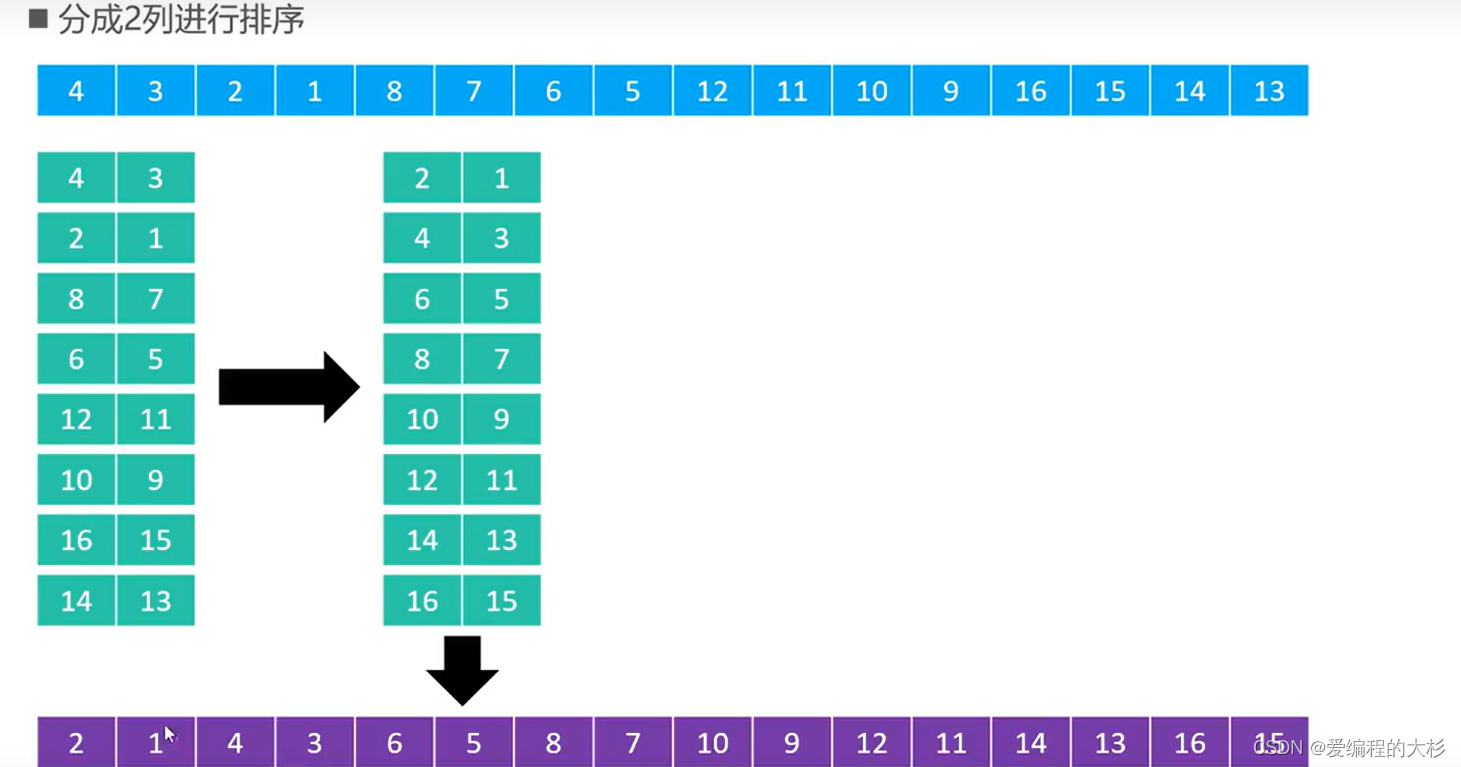
😂 比如，如果步长序列为{1,5,19,41,109,…}，就代表依次分成109列、41列、19列、5列、1列进行排序
2.希尔排序实例分析
上面的简单叙述可能还不能够充分理解希尔排序的原理；面我们通过几个实例进行探究
实例：
希尔本人给出发步长序列为n/2k,比如n为16时补偿序列就是{8，4，2，1}
将数组看成矩阵，按列不断进行排序
4.代码实现
public class ShellSort <E extends Comparable<E>> extends Sort<E>{
/**
* 希尔排序就是利用步长序列，将数组视为矩阵然后进行不断的列排序
*/
@Override
public void sort() {
//获取步长序列
List<Integer> stepSequence=shellStepSequence();
//根据步长序列进行分割排序
for(int step:stepSequence){
sort(step);
}
}
private List<Integer> shellStepSequence() {
//将每次二分长度作为步长序列的元素
List<Integer> stepSequence = new ArrayList<>();
int step = array.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}
//利用插入排序的排序的原理对数组矩阵的列进行排序
private void sort(int step){
//col :列
for(int col=0;col<step;col++)//对第几列进行排序
{
for(int begin=col+step;begin<array.length;begin+=step)
{
//一定要注意这里是
E cur=array[begin];
while(begin>col&&com(cur,array[begin-step])<0){
swap(begin,begin-step);
begin-=step;
}
}
}
}
}
