[数据结构与算法]算法提升：并查集的十个经典题目

目录

最长连续序列

被围绕的区域

岛屿数量

岛屿的最大面积

朋友圈问题

除法求值（hard）

情侣牵手（hard）

打砖块（hard）

最大人工岛（hard）

相似字符串组（hard）

最长连续序列

题目

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为?O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]

输出：4

解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]

输出：9

提示：

0 <= nums.length <= 105

-109 <= nums[i] <= 109

解析

并查集绝大多数的题目属于只要你知道有并查集这个东西就非常easy ，这个题之所以放在第一个就是想说并查集的强大。

1. 搞一个并查集把所有的节点初始化在里面；
2. 遍历每一个节点，如果key +1 也在存在，就把该节点挂在key+1 的节点下（union操作）
3. 遍历size map，看哪个key对应的size 最大；

代码

#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;

class UnionFind {
public:
    unordered_map<int,int> ancestor_; // 用来存储祖先的
    unordered_map<int, size_t> size_;  // 用来存储每一个集合的大小的

public:
    //并查集初始化
    UnionFind(const vector<int>& vec) {
        for(auto c:vec) {
            ancestor_.insert({c,c});
            size_.insert({c,1});
        }
    }

    // 查找元素属于哪一个集合
    int Find(int c) {
        //这里假设传入的字符C都是集合中已经存在的值
        int ancestor  = -1;
        int findc = c;
        while(ancestor!= findc) {
            ancestor = findc;
            findc = ancestor_[ancestor];
        }
        //这里可以做一个优化，把这个树化扁平，以减少未来的查找时间复杂度
        ancestor_[c] = ancestor;
        return ancestor;
    }

	
    void Union(int u1, int u2) {
        // 找到他们的祖先
        int anc1 = Find(u1);
        int anc2 = Find(u2);

        // 如果祖先相同就不做任何事情
        if (anc1 == anc2) return ;

        // 判断谁的size 大 && 若u1 size == u2 size，将u2挂在u1上
        int maxu = size_[anc1] >= size_[anc2] ? anc1:anc2;
        int minu = maxu == anc1? anc2:anc1;

        ancestor_[minu] = maxu;
    }
};


class solution {
public:
int function(vector<int> vec) {
        int max = 0;
        int maxkey  =0;
        UnionFind u = UnionFind(vec);
        for(auto [key,value]: u.ancestor_) {
            if (u.ancestor_.find(key+1)!=u.ancestor_.end()) {
                u.Union(key,key+1);
            }
        }
        for(auto [key,value]:u.size_) {
            if(max < value) {
                max = value;
                maxkey = key;
            }
        }
        return max;
}
};

被围绕的区域

力扣

题目

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

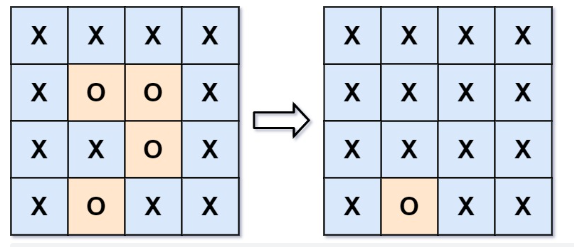
• 输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
• 输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
• 解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的?'O'?都不会被填充为?'X'。 任何不在边界上，或不与边界上的?'O'?相连的?'O'?最终都会被填充为?'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

• 输入：board = [["X"]]
• 输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

解析

题意：

• 本题中的矩阵一共有三种元素

• • x
  • 被x包围的o
  • 没有被x包围的o

• 本题要求将所有被x包围的o都变成x

分析：

• 由题意可以知道，关键在于区分两种不同状态的O。那么本题本质是：一个矩阵中有 3 个不同的元素，但是目前有2种元素（O）被混淆在一起，需要把这三种元素区分开来。
• 首先区分O和X很简单，关键是怎么区分“被x包围的o”和“没有被x包围的o”
• 题目中解释说：任何边界上的O都不会被填充为X。我们可以想到，所有的不被包围的O都直接或者间接的与边界上的O相连，因此问题转换为，如何寻找和边界联通的 O。
• 因此，我们可以用并查集的方法来做。那并查集中应该怎么区分两种状态的'O'呢？可以这样做：

• • 将那些与边界相连的'O'联通到一个虚拟节点dummy
  • 因此，那些不与dummy相连的就是不需要替换的'O'

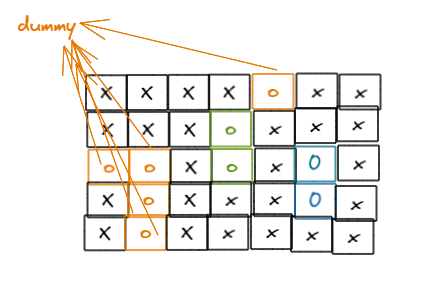
实现：

• UnionFind底层可以是多种数据结构，比如一维数组、二维数组、map......，这里我们用一维数组来实现
• 但是题目中给定的是一个二维矩阵，那么二维矩阵应该怎么用一维数据来表说呢？二维数组(x, y)可以转换成x * n + y 这个数(m是棋盘的行数，n是棋盘的列树)。这是二维坐标映射到一维的常用技巧
• 如何来表示dummy呢？我们将二维数组转换到一维数组，其坐标映射范围是索引[ 0， m ? n ? 1 ]，那么我们就让dummy占据索引m * n不就行了吗？
• 问题：为什么本题要选择使用一维数组来实现UnionFind？

• • 有因为 1 <= m, n <= 200，它比较小，预处理消耗的空间也比较小，用一维数组来实现不会有什么性能问题
  • 如果m * n比较大时，那么如果用一维数组来实现UnionFind会经历很重的初始化，这时建议用map

大流程：

• 定义一个指标转换函数

    static int index(int i, int j, int w){
        //x、y 表示二维坐标值，w 表示矩阵宽度。
        return i * w + j;
    }

• 初始化并查集，大小为矩阵的大小加一，多出的那一个作为所有边界节点的父节点dummy
• 遍历二维参数数组，如果当前值为O，说明它可能会被替换，这时候我们就要开始做区分了：

• • 如果当前O的横坐标或者纵坐标是边界索引，那么直接将当前O与dummy相连
  • 如果当前O不是边界节点，那么看它的上下左右，只要它的四周(有一个/多个)是O，就把它们之间打通。通过这样，如果有一个和边界直接或者间接的相连，那么就一定能联通dummy

• 再遍历一次二维数组，将与dummy不相连的O改成X

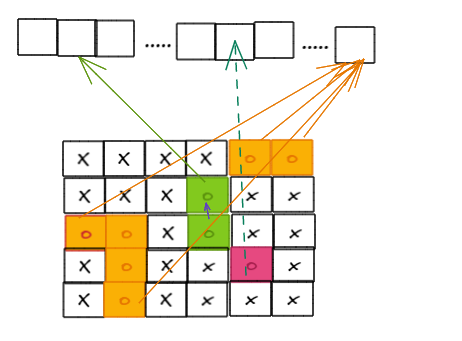
代码

class Solution {
    class UnionFind{
    private:
        std::vector<int> parent_;
        std::vector<int> size_;
        std::vector<int> help_;
        int cnt_;
    public:
        UnionFind(int N){
            cnt_ = N;
            parent_.resize(N);
            size_.resize(N);
            help_.resize(N);
            for (int i = 0; i < N; ++i) {
                parent_[i] = i;
                size_[i] = 1;
            }
        }

        void merge(int i,  int j){
            int ri = findRoot(i);
            int rj = findRoot(j);
            if(ri != rj){
                if(size_[ri] >= size_[rj]){
                    parent_[rj] = ri;
                    size_[ri] += size_[rj];
                }else{
                    parent_[ri] = rj;
                    size_[rj] += size_[ri];
                }
                --cnt_;
            }
        }

        bool isConnected(int i, int j){
            return findRoot(i) == findRoot(j);
        }
    private:
        int findRoot(int i){
            int hi = 0;
            while (parent_[i] != i){
                help_[hi++] = i;
                i = parent_[i];
            }
            for (hi--;  hi >= 0; --hi) {
                parent_[help_[hi]] = i;
            }
            return i;
        }
    };

private:
    static int index(int i, int j, int w){
        //x、y 表示二维坐标值，w 表示矩阵宽度。
        return i * w + j;
    }
public:
    void solve(vector<vector<char>>& board) {
        if(board.empty()){
            return;
        }

        int m = board.size();         // 矩阵行数
        int n = board[0].size();      // 矩阵列数(宽度)，即第一行元素数
        UnionFind unionFind(m * n + 1);          //  初始化并查集，大小为矩阵大小+1, 给 dummy 留?个额外位置
        int dummy = m * n;              // dummy索引


        // 与边角上的`O`相连的 O 与 dummy 连通
        std::vector<std::vector<int>> dirs {{1, 0},{-1, 0},{0, 1}, {0, -1}};
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == 'O') {
                    // 边界节点是O
                    if (i == 0 || j == 0 || i == m - 1 || j == n - 1) {
                        unionFind.merge(index(i, j, n), dummy);
                    } else {
                        // 非边界节点是O，那么看它上下左右是否有O
                        for (auto dir : dirs) {
                            int x = i + dir[0];
                            int y = j + dir[1];
                            if (board[x][y] == 'O') {  //如果是，那么将它们打通
                                unionFind.merge(index(i, j, n), index(x, y, n));
                            }
                        }
                    }
                }
            }
        }



        // 所有不和 dummy 连通的 O， 都要被替换
        for (int i = 1; i < m - 1; i++){
            for (int j = 1; j < n - 1; j++){
                if (board[i][j] == 'O'){
                    if (!unionFind.isConnected(index(i, j, n), dummy)){
                        board[i][j] = 'X';
                    }
                }
            }
        }
    }
};

岛屿数量

力扣

题目

给你一个由?'1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 '0' 或 '1'

解析

• 题目要求：找到矩阵中 “岛屿的数量” ，上下左右相连的 1 都被认为是连续岛屿。
• 怎么找呢？我们可以将所有相连的1都打通，最后数有几个联通分量即可
• 因此，我们用并查集来解决这个问题。UnionFind底层可以是多种数据结构，比如一维数组、二维数组、map......，这里我们用一维数组来实现，其大致流程如下：

• • 遍历给定的二维数组，将所有的1都看成是一个单独的岛屿
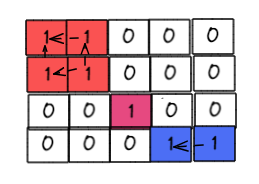
  • 然后将上下所有相连的1都打通：

• • • 遍历给定的二维数组，对于每一个1，只看它的左边和上边，如果发现有1，就做merge操作（为甚只看左边和上边，因为右边和下边是对称的，而我们从左到右，从上到下遍历，所以不会重复和遗落）

• 比如，示例二中从下图中我们可以看出，一共有3个联通分离，所以一共有三个岛屿

代码

class Solution {


    class UnionFind{
    private:
        std::vector<int> parent_;
        std::vector<int> size_;
        std::vector<int> help_;
        int cnt_{};
        int wid_;
        
        int index(int i, int j) const{
            return i * wid_ + j;         //x、y 表示二维坐标值，w 表示矩阵宽度。
        }

        int findRoot(int i){
            int hi = 0;
            while (parent_[i] != i){
                help_[hi++] = i;
                i = parent_[i];
            }
            for (hi--;  hi >= 0; --hi) {
                parent_[help_[hi]] = i;
            }
            return i;
        }
    public:
        explicit UnionFind(vector<vector<char>>& board){
            int m = board.size();         // 矩阵行数
            int n = board[0].size();      // 矩阵列数(宽度)，即第一行元素数
            parent_.resize(m * n);
            size_.resize(m * n);
            help_.resize(m * n);
            wid_ = n;
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    if(board[i][j] == '1'){
                        int idx = index(i, j);
                        parent_[idx] = idx;
                        size_[idx] = 1;
                        ++cnt_;
                    }
                }
            }
        }

        void merge(int i1,  int j1, int i2, int j2){
            int i = index(i1, j1);
            int j = index(i2, j2);
            int ri = findRoot(i);
            int rj = findRoot(j);
            if(ri != rj){
                if(size_[ri] >= size_[rj]){
                    parent_[rj] = ri;
                    size_[ri] += size_[rj];
                }else{
                    parent_[ri] = rj;
                    size_[rj] += size_[ri];
                }
                --cnt_;
            }
        }

        int count() const {
            return cnt_;
        }

        bool isConnected(int i, int j){
            return findRoot(i) == findRoot(j);
        }
    };


public:
    int numIslands(vector<vector<char>>& board) {
        if(board.empty()){
            return 0;
        }

        int m = board.size();         // 矩阵行数
        int n = board[0].size();      // 矩阵列数(宽度)，即第一行元素数

        UnionFind unionFind(board);

        // 第一列（除了(0, 0)外）
        for (int i = 1; i < m; ++i) {
            if(board[i - 1][0] == '1' && board[i][0] == '1'){
                unionFind.merge(i - 1, 0, i, 0);
            }
        }

        // 第一行（除了(0, 0)外）
        for (int j = 1; j < n; ++j) {
            if(board[0][j - 1] == '1' && board[0][j] == '1'){
                unionFind.merge(0, j - 1, 0, j);
            }
        }

        
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if(board[i][j] == '1' ){  //  只看左&上
                    if(board[i - 1][j] == '1'){
                        unionFind.merge(i, j, i - 1, j);
                    }
                    if(board[i][j - 1] == '1'){
                        unionFind.merge(i, j, i, j - 1);
                    }
                }
            }
        }

        return unionFind.count();
    }
};

岛屿的最大面积

力扣

题目

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿?是由一些相邻的?1?(代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设?grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

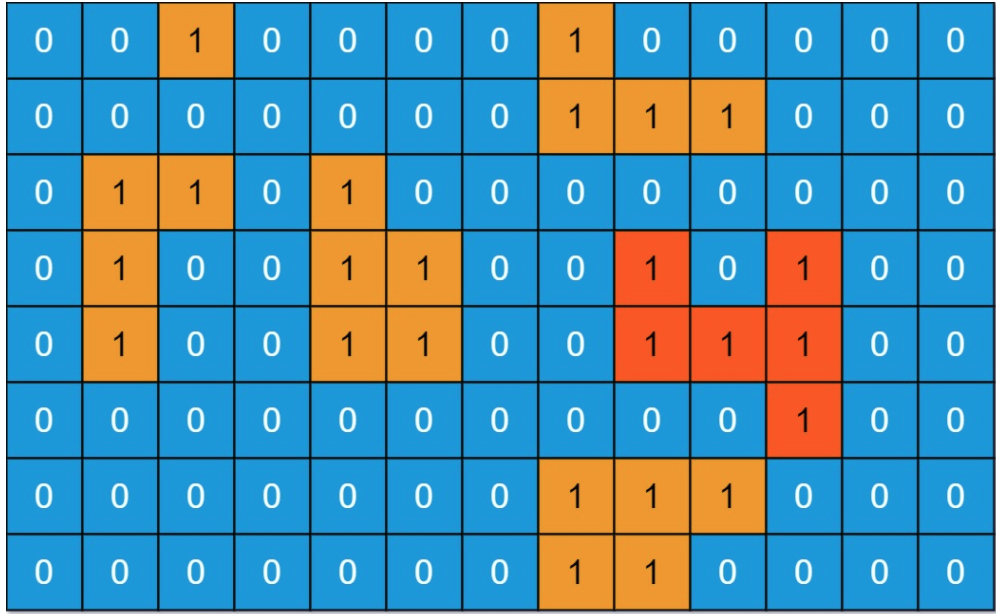
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

输出：6

解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]

输出：0

提示：

m == grid.length

n == grid[i].length

1 <= m, n <= 50

grid[i][j] 为 0 或 1

解析

岛屿问题升级版本，一个非常典型的并查集题目，用并查集把相邻点一合并，然后提取最大size 的集合，输出size。

当然也可以使用图的遍历算法做。

代码

class Solution {
private:
    vector<vector<pair<int,int>>>ancestor_;
    vector<vector<int>> size_;

public:
    bool isZeroAll (vector<vector<int>>& grid) {

        for(auto line :grid) {
            for(int i : line) {
                if (i!=0) return false;
            }
        }
        return true;
    }
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        if(isZeroAll(grid)) return 0;
        init(grid);
        for(int i = 0 ; i<grid.size();i++) {
            for(int j= 0;j<grid[0].size();j++) {
                if(grid[i][j] == 1 ) {
                    if(i+1 < grid.size() && grid[i+1][j] == 1) merge({i,j},{i+1,j});
                    if(j+1 < grid[0].size() && grid[i][j+1] == 1) merge({i,j},{i,j+1});
                }
            }
        }
        int max =0;
        for(auto line : size_) {
            for(int size : line) {
                max = max>=size? max:size;
            }
        }
    return max;
    }

    void init(vector<vector<int>>& grid) {
        ancestor_.resize(grid.size());
        size_.resize(grid.size());
        
        for(int i = 0; i < grid.size();i++ ) {
            ancestor_[i].resize(grid[0].size());
            size_[i].resize(grid[0].size());
            for(int j = 0;j<grid[0].size();j++) {
                ancestor_[i][j] = {i,j};
                size_[i][j] = 1;
            }
        }

    }
    pair<int,int> findAncestor(pair<int,int> point) {
        pair<int,int> p = point;
        while(1) {
            pair<int,int>  anc = ancestor_[p.first][p.second];
            if(anc.first == p.first && anc.second == p.second) {
                return p;
            }
            p = anc;
        }

    }

    void merge(pair<int,int> p1, pair<int,int> p2) {
        pair<int,int> a1 = findAncestor(p1);
        pair<int,int> a2 = findAncestor(p2);
        if(a1 == a2) return;
        pair<int,int> amax = size_[a1.first][a1.second] > size_[a2.first][a2.second]?ancestor_[a1.first][a1.second] :ancestor_[a2.first][a2.second] ;
        pair<int,int> amin = amax == ancestor_[a1.first][a1.second]?ancestor_[a2.first][a2.second]:ancestor_[a1.first][a1.second];
        size_[amax.first][amax.second] += size_[amin.first][amin.second];
     //   size_[amin.first][amin.second] = 0;
        ancestor_[amin.first][amin.second] = {amax.first,amax.second};

    }
};

朋友圈问题

力扣

题目

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1：

• 输入：

[[1,1,0],

[1,1,0],

[0,0,1]]

• 输出：2
• 解释：已知学生 0 和学生 1 互为朋友，他们在一个朋友圈。

第2个学生自己在一个朋友圈。所以返回 2 。

示例 2：

• 输入：

[[1,1,0],

[1,1,1],

[0,1,1]]

• 输出：1
• 解释：已知学生 0 和学生 1 互为朋友，学生 1 和学生 2 互为朋友，所以学生 0 和学生 2 也是朋友，所以他们三个在一个朋友圈，返回 1 。

提示：

• 1 <= N <= 200
• M[i][i] == 1
• M[i][j] == M[j][i]

解析

题意：给定一个二维数组，它一定是一个正方形

• 二维数组的索引可以看成是朋友圈的编号
• 二维数组的值表示朋友之间的关系：1表示认识，0表示不认识

• • M[i][j] = 1，表示i认识j
  • 由题意可以推测，M[i][j] = 1，那么M[j][i]也为1，也就是j认识i

• 也就是说：

• • 对角线一定全是1，因为自己是认识自己的

• • • M[i][i] = 1

• • 而且这个矩阵是对称的

• • • M[i][j] = 1
    • M[i][j] = 1

• 求有几个朋友圈？

分析：

• 这是一道经典的并查集问题。举个例子，如下图
• 我们先根据二维数组生成一个并查集。
• 刚开始时，有集合（{1}）、（{2}）、（{3}）、（{4}
• 然后一行行遍历数组

• • 刚开始第一行，对于0：

• • • 0和0是认识自己的，之前已经有了(0)，不用管
    • 0和1不认识，不用管
    • 0和2认识，因此(0)合并（{2}），得到{（0，2）}
    • 0和3不认识，不用管
    • 0和4认识，因此(0)合并（{2, 4}），得到{（0，2, 4）}

• • 然后第二行，对于1：

• • • 1和0不认识
    • 1和1认识，之前已经有了(1)，不用管
    • 1和2不认识
    • 1和3认识，合并（{1}）（{3}）得到{（1，3）}
    • 1和4不认识

• • 然后第三行，对于2：

• • • 2和0认识：原来应该得到{(2，0)}，这个{(2，0)}已经在第一行中出现过了，所以不用管
    • 2和1不认识，不用管
    • 2自己认识自己，不用管
    • .....

• • 然后第四行，对于3，同上
  • 最后第五行，对于4，同上

• 也就是说：最终生成了两个集合： ${（0，2、4）、（1，3）}$，所以朋友圈的个数是2
• 又因为这个矩阵高度对称，所以根据这个集合生成并查集时，只遍历右上角或者左下角就可以了

流程：

• 先根据N生成集合{0}、{1}、{2}、{3}......{N-1}
• 遍历矩阵的右上角，如果发现M[i][j] == 1，那么就将i和j合并
• 最终返回联通量

代码

class Solution {
    class UnionFind{
    private:
        std::vector<int> parent_; // parent[i] = k ： i的父亲是k
        std::vector<int> size_;   // size[i] = k ： 如果i是代表节点，size[i]才有意义( i所在的集合大小是多少)，否则无意义
        std::vector<int> help_;  //  辅助结构
        int cnt_;               //一共有多少个集合
        
    public:
        explicit UnionFind(int n){
            cnt_ = n;
            parent_.resize(n);
            size_.resize(n);
            help_.resize(n);
            for (int i = 0; i < n; ++i) {
                parent_[i] = i;
                size_[i] = 1;
            }
        }

        // 返回i的代表节点
        // 这个过程要做路径压缩
        int findRoot(int i){
            int hi = 0;
            while (i != parent_[i]){
                help_[hi++] = parent_[i];
                i = parent_[i];
            }
            for (hi--; hi >= 0; --hi) {
                parent_[help_[hi]] = i;
            }
            return i;
        }

        void merge(int i, int j){
            int f1 = findRoot(i);
            int f2 = findRoot(j);
            if(f1 != f2){
                if(size_[f1] >= size_[f2]){
                    parent_[f2] = f1;
                    size_[f1] = size_[f1] + size_[f2];
                }else{
                    parent_[f1] = f2;
                    size_[f2] = size_[f2] + size_[f1];
                }
                --cnt_;
            }
        }

        int counts() const{
            return cnt_;
        }
    };
    
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int N = isConnected.size();
        UnionFind unionFind(N);   //先初始化集合： {0} {1} {2} {N-1}
        // 遍历这个二维数组的右上角
        for (int i = 0; i < N; ++i) {
            for (int j = i + 1; j < N; ++j) {
                if(isConnected[i][j] == 1){  // i和j相互认识就合并
                    unionFind.merge(i, j);
                }
            }
        }

        // 有多少个集合就表示有多少个朋友圈
        return unionFind.counts();
    }
};

除法求值（hard）

力扣

题目

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

示例 1：

输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]

输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]

解释：

条件：a / b = 2.0, b / c = 3.0

问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?

结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]

示例 2：

输入：equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]

输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：

输入：equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]

输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：

1 <= equations.length <= 20

equations[i].length == 2

1 <= Ai.length, Bi.length <= 5

values.length == equations.length

0.0 < values[i] <= 20.0

1 <= queries.length <= 20

queries[i].length == 2

1 <= Cj.length, Dj.length <= 5

Ai, Bi, Cj, Dj 由小写英文字母与数字组成

解析

本题用图来实现算mid级别的难度，但是如果用并查集就是hard级别。

这个题目看到了二维数组：equations、queries，一个代表给出的条件，一个代表要求的内容，大概的思路就是从equations 中的除法关系推出queries的关系，这里有一个很重要的信息，就是“除法”，加减乘除都是属于四则运算，只要是单个符号出现，或者加减一起出现或者乘除一起出现都是满足结合率和分配律的，换句话说就是具备传染性。

二维数组，元素之间的关系具备传染性，且可以得到两个元素之间的关系（不是权），典型的图论解决的范畴，所以在这个题目中，可以直接使用图的搜索算法做：

1. 构建一个双向图，然后需要存储双向的关系，比如说a/b = 2， 那么a - > b = 2, b->a = 0.5；
2. 把图关系建立完毕之后，从queries 中找到一个值：x，然后开始广度寻找（为什么使用广度，因为在这里效率高）；
3. 直到找到queries 中y值，然后把路过的关系相乘，如果遍历完找不到y，就返回 -1，结束；

PS：

1. 可以在构建图的时候搞一个hash，在queries 的时候先看数在不在。

1. 需要在走过一个节点的时候标记这个节点已经走过了，不然会陷入无限循环。

解决之后开始想优化方法：

求最短路径：从有向图找路径这个题目来说，首先想到的就是上面做的BFS、DFS这样的搜索算法，然后稍微高级一点就是找找最短路径，这里是不带权的最短路径，所以一些经典的算法基本上都可以使用，比如prim、狄杰斯特拉、弗洛伊德之类的；

但是不管再怎么求最短路径其实都是有时间复杂度都是比较高的，所以可以考虑用空间去换时间，这里可以使用到带权的并查集。

带权并查集的使用思路很简单：

比如 x/y = A，x的节点作为头和y的节点合并 权值设置为A；

之后 z/y = B，那么z节点、y节点分别去现有集合find，发现y在之前的集合中已经存在，然后这一对变量就直接加入，并换算得到x/z = A/B，然后x的祖先就是x，y、z 的祖先均为x。

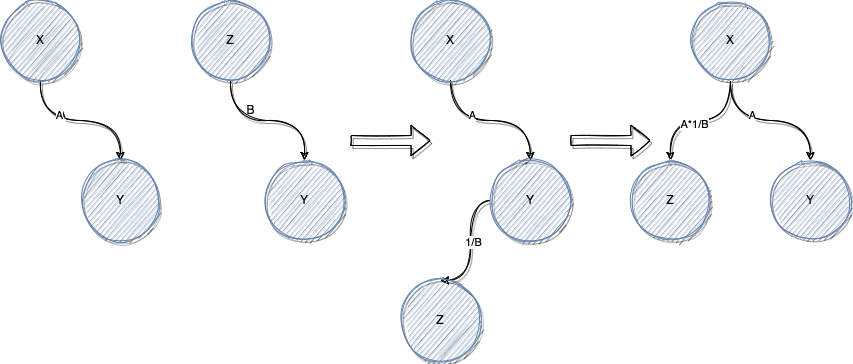
如果 之后来的是m/n = C，m与n的祖先都是自己，与之前的集合没有公共祖先，就自己形成一个集合 n的祖先为m；

然后来了 m/x = D, m的祖先是自己，是一个集合，x的祖先也是自己，也是一个集合，就将两个集合合并；

最后讲形成多个集合，每个集合都有一个公共祖先。

queries 中取出数后，就可以直接看两个数是不是同一个祖先，如果是的话，就可以直接计算拿出结果，如果不是一个公共祖先就返回 -1.

这样的话查找的时间复杂度会非常低，变成常数时间O（1）

代码

class Solution {
public:
    int findf(vector<int>& f, vector<double>& w, int x) {
        if (f[x] != x) {
            int father = findf(f, w, f[x]);
            w[x] = w[x] * w[f[x]];
            f[x] = father;
        }
        return f[x];
    }

    void merge(vector<int>& f, vector<double>& w, int x, int y, double val) {
        int fx = findf(f, w, x);
        int fy = findf(f, w, y);
        f[fx] = fy;
        w[fx] = val * w[y] / w[x];
    }

    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        int nvars = 0;
        unordered_map<string, int> variables;

        int n = equations.size();
        for (int i = 0; i < n; i++) {
            if (variables.find(equations[i][0]) == variables.end()) {
                variables[equations[i][0]] = nvars++;
            }
            if (variables.find(equations[i][1]) == variables.end()) {
                variables[equations[i][1]] = nvars++;
            }
        }
        vector<int> f(nvars);
        vector<double> w(nvars, 1.0);
        for (int i = 0; i < nvars; i++) {
            f[i] = i;
        }

        for (int i = 0; i < n; i++) {
            int va = variables[equations[i][0]], vb = variables[equations[i][1]];
            merge(f, w, va, vb, values[i]);
        }
        vector<double> ret;
        for (const auto& q: queries) {
            double result = -1.0;
            if (variables.find(q[0]) != variables.end() && variables.find(q[1]) != variables.end()) {
                int ia = variables[q[0]], ib = variables[q[1]];
                int fa = findf(f, w, ia), fb = findf(f, w, ib);
                if (fa == fb) {
                    result = w[ia] / w[ib];
                }
            }
            ret.push_back(result);
        }
        return ret;
    }
};

情侣牵手（hard）

力扣

题目

n 对情侣坐在连续排列的 2n?个座位上，想要牵到对方的手。

人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的 ID。情侣们按顺序编号，第一对是?(0, 1)，第二对是?(2, 3)，以此类推，最后一对是?(2n-2, 2n-1)。

返回 最少交换座位的次数，以便每对情侣可以并肩坐在一起。 每次交换可选择任意两人，让他们站起来交换座位。

示例 1:

输入: row = [0,2,1,3]

输出: 1

解释: 只需要交换row[1]和row[2]的位置即可。

示例 2:

输入: row = [3,2,0,1]

输出: 0

解释: 无需交换座位，所有的情侣都已经可以手牵手了。

提示:

2n == row.length

2 <= n <= 30

n?是偶数

0 <= row[i] < 2n

row?中所有元素均无重复

解析

这个题目作为hard 有点名不副实，只需要搞明白一个点就很清晰了。

那就是 （2i，2i+1）构成一对情侣，所以可以给情侣对编号，比如N这个value就属于N/2 这个情侣对

步骤：（假设就是数组下标% 2 等于0的为女朋友、为1的是男朋友）

1. 遍历数组找到女朋友，求出该值对应的情侣对，然后检查本来应该出现男朋友的位置，现在是哪个情侣对的
2. 将这两个情侣对进行 merge，代表需要把人交换过来；
3. 将所有的情侣对都遍历一遍之后，提取所有的集合，将集合的size - 1 ，就是要交换的次数

代码

class Solution {
private:
    vector<int>ancestor_;
    vector<int>size_;

public:
    int minSwapsCouples(vector<int>& row) {
        init(row);
        for(int i =0;i<row.size();i+=2) {
            merge(row[i]/2,row[i+1]/2);
        }
        int count = 0;
        for(int s :size_) {
            count+=(s-1);
        }
        return count;
    }

    void init(vector<int>& row) {
        ancestor_.resize(row.size()/2);
        size_.resize(row.size()/2);
        for(int i =0;i<row.size()/2;i++) {
            ancestor_[i] = i;
            size_[i] =1;
        }
    }
    int findAncestor(int point) {
        int p = point;
        while(1) {
            int  anc = ancestor_[p];
            if(anc == p) {
                return p;
            }
            p = anc;
        }

    }

    void merge(int p1, int p2) {
        int a1 = findAncestor(p1);
        int a2 = findAncestor(p2);
        if(a1 ==a2) return;
        int amax = size_[a1] > size_[a2]?ancestor_[a1] :ancestor_[a2] ;
        int amin = amax == ancestor_[a1]?ancestor_[a2]:ancestor_[a1];
        size_[amax] += size_[amin];
        size_[amin] = 1;
        ancestor_[amin] =amax;

    }
};

打砖块（hard）

力扣

题目

有一个 m x n 的二元网格?grid?，其中 1 表示砖块，0 表示空白。砖块 稳定（不会掉落）的前提是：

• 一块砖直接连接到网格的顶部，或者
• 至少有一块相邻（4?个方向之一）砖块 稳定 不会掉落时

给你一个数组 hits ，这是需要依次消除砖块的位置。每当消除?hits[i] = (rowi, coli) 位置上的砖块时，对应位置的砖块（若存在）会消失，然后其他的砖块可能因为这一消除操作而 掉落 。一旦砖块掉落，它会 立即 从网格?grid?中消失（即，它不会落在其他稳定的砖块上）。

返回一个数组 result ，其中 result[i] 表示第 i 次消除操作对应掉落的砖块数目。

注意，消除可能指向是没有砖块的空白位置，如果发生这种情况，则没有砖块掉落。

示例 1：

• 输入：grid = [[1,0,0,0],[1,1,1,0]], hits = [[1,0]]
• 输出：[2]
• 解释：网格开始为：

[[1,0,0,0]，

[1,1,1,0]]

消除 (1,0) 处加粗的砖块，得到网格：

[[1,0,0,0]

[0,1,1,0]]

两个加粗的砖不再稳定，因为它们不再与顶部相连，也不再与另一个稳定的砖相邻，因此它们将掉落。得到网格：

[[1,0,0,0],

[0,0,0,0]]

因此，结果为 [2] 。

示例 2：

• 输入：grid = [[1,0,0,0],[1,1,0,0]], hits = [[1,1],[1,0]]
• 输出：[0,0]
• 解释：网格开始为：

[[1,0,0,0],

[1,1,0,0]]

消除 (1,1) 处加粗的砖块，得到网格：

[[1,0,0,0],

[1,0,0,0]]

剩下的砖都很稳定，所以不会掉落。网格保持不变：

[[1,0,0,0],

[1,0,0,0]]

接下来消除 (1,0) 处加粗的砖块，得到网格：

[[1,0,0,0],

[0,0,0,0]]

剩下的砖块仍然是稳定的，所以不会有砖块掉落。

因此，结果为 [0,0] 。

解析

分析：

（1）什么样子的【砖块】不会掉落？

• 两种可能：

• • 【砖块】位于第0行
  • 与第0行的【砖块】直接或者间接的相连

（2）每一枪（hits[i]）会带来什么后果？

• 当前位置[hits[i][0]，hits[i][1]]不是【砖块】，没有影响
• 当前位置是[hits[i][0]，hits[i][1]]【砖块】，那么有如下可能：

• • 仅仅打碎了【当前砖块】
  • 除了打碎了【当前砖块】，还有一些【砖块】需要掉落

（3）打碎和掉落分别是什么意思？

• 我们无法收集到被打碎的砖块
• 一旦砖块掉落：

• • 它会立即从网格中消失，被我们收集到（它不会落在其他稳定的砖块上），意思是下面的这种情况不会出现
  • 我们这时会收集到2个掉落的砖块

（4）如何判断砖块是否会掉落呢？

• 和玩打砖块游戏一样，设置一个天花板，如果敲掉之后一组不再和天花板连接，它们就会掉下来
• 于是一种很直观的思路如下：

• • 把所有的砖块建立一个并查集，集合的数量肯定为1
  • 每敲掉一个地方，把它和四周的砖块断开连接
  • 断开后原来的集合可能变成多块，也可能还是一块
  • 判断哪块会掉落并求所有掉落连通块的大小

（5）上面的思路有什么问题？

• 断开连接：

• • 并查集擅长的事情是合并集合，而不是断开集合。
  • 因为在合并的过程中会有节点之间连接信息的损失，比如添加一条即将成环的边的时候，或者在做路径压缩的时候

（6）怎么办？

• 可以逆向思考，利用并查集擅长合并的特点，从最后一次敲砖块，向前进行合并

• • 预先敲掉要敲掉的所有砖块，把剩下的砖块建立并查集
  • 从最后一次敲击开始向前遍历

• • • 填回被敲掉的砖
    • 和上下左右四个邻居的砖块合并
    • 合并后-合并前的数量就是这次掉落的数量

• 即反过来思考，将问题打碎砖块会掉落多少个砖块转化成补上砖块会新增多少个砖块粘到房顶

思路：这道题我们可以用接在天花板上的砖的数量变化为收集答案

看个例子：

（1）先预处理grid

• 正序遍历hits，预先敲掉要敲掉的所有砖块

• • 如果发现某个位置真的有砖块，那么就将这个位置变为2
  • 如果没有砖块，不用关心，因为它不会影响最终的结果

（2）把剩下的砖块建立并查集

• 这里并查集的底层数据结构我们用二维数组来实现
• 遍历grid，对每一个1独立做成一个集合

• • 一开始，每一个1都是一个小集合，只属于自己，谁也不和谁相连
  • 在并查集中增加一个结构，让集合拥有一个属性：该集合是否与天花板相连。初始时，第0行的集合都与天花板相连
  • 在并查集中，还需要额外记录现在天花板上一共有多少个砖头

• 对每一个集合上下左右合并

• • 让所有的1合并
  • 注意，合并的过程中注意要更新属性和天花板连接的砖头数量

（3）逆序遍历hits，补上砖块，计算出会增多少个砖块粘到房顶

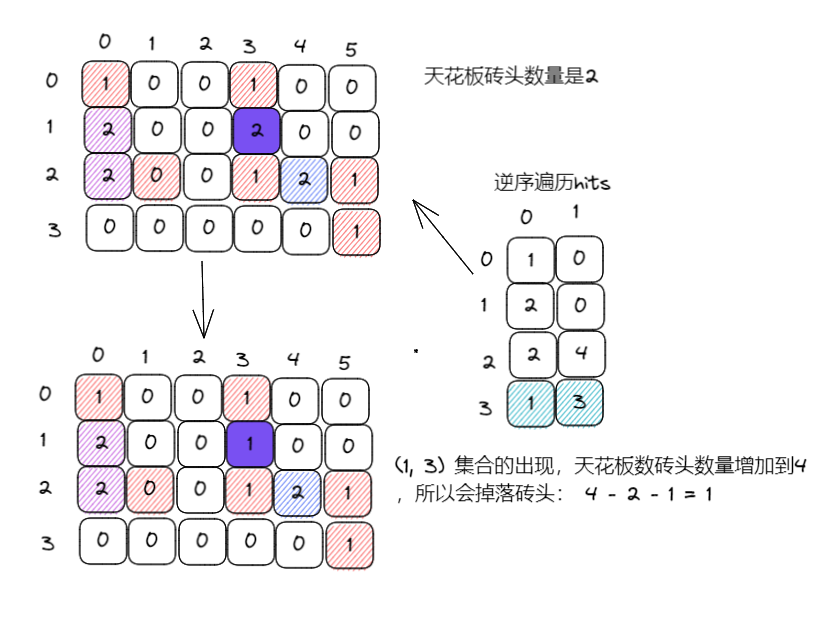
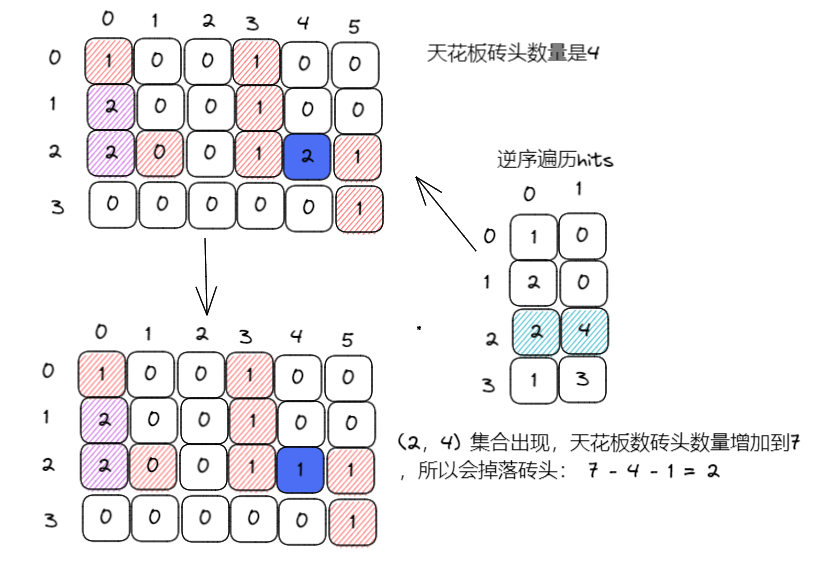
（3）很明显，hit的位置导致砖头掉落要分情况讨论

• 如果遍历hits发现某个grid不是2，说明打到了空白上，这个时候不会引起集合合并，什么也不会影响
• 如果遍历hits发现某个grid是2，说明这个地方原本是有砖块的，那么掉落砖块数量 = now - pre - 1

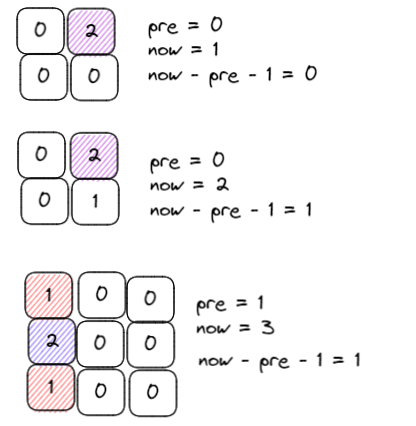
代码

class Solution {
    class UnionFind {
        int N;
        int M_;
        int cellingAll_; // 有多少块砖，连到了天花板上
        vector<vector<int>> grid_; // 原始矩阵，因为炮弹的影响，1 -> 2
        std::vector<bool> cellingSet_;// cellingSet_[i] = true; i 是头节点，所在的集合是天花板集合
        std::vector<int> parent_;
        std::vector<int> size_;
        std::vector<int> help_;

        void initSpace(vector<vector<int>> &matrix) {
            grid_ = matrix;
            N = grid_.size(), M_ = grid_[0].size();
            int all = N * M_;
            cellingAll_ = 0;
            cellingSet_.resize(all);
            parent_.resize(all);
            size_.resize(all);
            help_.resize(all);
            for (int row = 0; row < N; ++row) {
                for (int col = 0; col < M_; ++col) {
                    if (grid_[row][col] == 1) {
                        int index = row * M_ + col;
                        parent_[index] = index;
                        size_[index] = 1;
                        if (row == 0) {
                            cellingSet_[index] = true;
                            cellingAll_++;
                        }
                    }
                }
            }
        }

        void initConnect(){
            for (int row = 0; row < N; ++row) {
                for (int col = 0; col < M_; ++col) {
                    merge(row, col, row - 1, col);
                    merge(row, col, row + 1, col);
                    merge(row, col, row, col - 1);
                    merge(row, col, row, col + 1);
                }
            }
        }

        bool valid(int row, int col) {
            return row >= 0 && row < N && col >= 0 && col < M_ && grid_[row][col] == 1;
        }

        void merge(int r1, int c1, int r2, int c2) {
            if(valid(r1, c1) && valid(r2, c2)){
                int father1 = find(r1, c1);
                int father2 = find(r2, c2);
                if(father1 != father2){
                    int size1 = size_[father1];
                    int size2 = size_[father2];
                    bool status1 = cellingSet_[father1];
                    bool status2 = cellingSet_[father2];
                    if (size1 <= size2) {
                        parent_[father1] = father2;
                        size_[father2] = size1 + size2;
                        if (status1 ^ status2) {
                            cellingSet_[father2] = true;
                            cellingAll_ += status1 ? size2 : size1;
                        }
                    } else {
                        parent_[father2] = father1;
                        size_[father1] = size1 + size2;
                        if (status1 ^ status2) {
                            cellingSet_[father1] = true;
                            cellingAll_ += status1 ? size2 : size1;
                        }
                    }
                }


            }
        }

        int find(int row, int col){
            int stackSize = 0;
            int idx = row * M_ + col;
            while (idx != parent_[idx]){
                help_[stackSize++] = idx;
                idx = parent_[idx];
            }
            while (stackSize != 0){
                parent_[help_[--stackSize]] = idx;
            }
            return idx;
        }

    public:
        UnionFind(vector<vector<int>> &matrix) {
            initSpace(matrix);
            initConnect();
        }

        int cellingNum() {
            return cellingAll_;
        }


        int finger(int row, int col){
            // 填上grid
            grid_[row][col] = 1;
            // 对当前行对应的那个集合操作
            int cur = row * M_ + col;  // 这个位置对应的集合
            if (row == 0) {  // 如果当前是天花板上的砖块
                cellingSet_[cur] = true;
                cellingAll_++;
            }

            parent_[cur] = cur;
            size_[cur] = 1;
            int pre = cellingAll_;
            merge(row, col, row - 1, col);
            merge(row, col, row + 1, col);
            merge(row, col, row, col - 1);
            merge(row, col, row, col + 1);
            int now = cellingAll_;
            if (row == 0) { 
                return now - pre;  //pre之前已经加过1了
            } else {  
                return now == pre ? 0 : now - pre - 1;
            }
        }
    };
public:
    vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {
        // 预处理，正序敲掉砖块
        for (int i = 0; i < hits.size(); ++i) {
            if (grid[hits[i][0]][hits[i][1]] == 1) {
                grid[hits[i][0]][hits[i][1]] = 2;
            }
        }

        // 逆序补回砖块
        UnionFind unionFind  (grid);
        std::vector<int> ans(hits.size());
        for (int i = hits.size() - 1; i >= 0; --i) {
            if (grid[hits[i][0]][hits[i][1]] == 2) {  // 只有当前位置有砖块时才去合并
                ans[i] = unionFind.finger(hits[i][0], hits[i][1]);
            }
        }
        return ans;
    }
};

最大人工岛（hard）

力扣

题目

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格?0 变成?1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的?1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]

输出: 3

解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

输入: grid = [[1, 1], [1, 0]]

输出: 4

解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: grid = [[1, 1], [1, 1]]

输出: 4

解释: 没有0可以让我们变成1，面积依然为 4。

提示：

n == grid.length

n == grid[i].length

1 <= n <= 500

grid[i][j] 为 0 或 1

解析

首先看到二维数组就可以直接想到图算法，图算法中最常见的算法就是BFS、DFS，本题也确实可以使用图的遍历算法做：

使用遍历图中为0的节点，假设反转为1然后利用BFS做面积计算，直到找完全部的值，然后求最大值作为面积。

然后就是优化，每一个节点都去做图的遍历找面积，有很多浪费的步骤：

1. 假设a、b两个几点都挨着同一片岛，那么遍历a的时候会遍历一次面积，b的时候又会遍历一次面积；
2. 假设a是一个孤立点，旁边没有点，那它就算是反转了也无济于事；

上述的重点就是第一个，重复遍历岛的面积，所以需要一个数据结构把之前的岛的面积存下来，那么就可以顺理成章的使用并查集做这个工作了；

步骤：

1. 遍历每一个点，找联通域，利用并查集形成岛集合；
2. 遍历每一个点，判断是否为非孤立空白点2；

1. 1. 若不是跳过
   2. 若是，找上下左右4个点的祖先（属于哪个岛集合），然后把不同岛的岛size相加，记录 （max> =nowSize ? max:nowSize）

1. 输出最大值

代码

class Solution {
public:
    const static inline vector<int> dirs = {-1, 0, 1, 0, -1};

    int largestIsland(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<int> p(n * n);
        vector<int> size(n * n, 1);
        iota(p.begin(), p.end(), 0);

        function<int(int)> find;
        find = [&](int x) {
            if (p[x] != x) {
                p[x] = find(p[x]);
            }
            return p[x];
        };

        int ans = 1;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) {
                    for (int k = 0; k < 4; ++k) {
                        int x = i + dirs[k], y = j + dirs[k + 1];
                        if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y]) {
                            int pa = find(x * n + y), pb = find(i * n + j);
                            if (pa == pb) continue;
                            p[pa] = pb;
                            size[pb] += size[pa];
                            ans = max(ans,size[pb]);
                        }
                    }
                }
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (!grid[i][j]) {
                    int t = 1;
                    unordered_set<int> vis;
                    for (int k = 0; k < 4; ++k) {
                        int x = i + dirs[k], y = j + dirs[k + 1];
                        if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y]) {
                            int root = find(x * n + y);
                            if (!vis.count(root)) {
                                vis.insert(root);
                                t += size[root];
                            }
                        }
                    }
                    ans = max(ans, t);
                }
            }
        }
        return ans;
    }
};

相似字符串组（hard）

题目

如果交换字符串?X 中的两个不同位置的字母，使得它和字符串?Y 相等，那么称 X 和 Y 两个字符串相似。如果这两个字符串本身是相等的，那它们也是相似的。

例如，"tars" 和 "rats" 是相似的 (交换 0 与 2 的位置)；?"rats" 和 "arts" 也是相似的，但是 "star" 不与 "tars"，"rats"，或 "arts" 相似。

总之，它们通过相似性形成了两个关联组：{"tars", "rats", "arts"} 和 {"star"}。注意，"tars" 和 "arts" 是在同一组中，即使它们并不相似。形式上，对每个组而言，要确定一个单词在组中，只需要这个词和该组中至少一个单词相似。

给你一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个字母异位词。请问 strs 中有多少个相似字符串组？

?示例 1：

• 输入：strs = ["tars","rats","arts","star"]
• 输出：2

示例 2：

• 输入：strs = ["omv","ovm"]
• 输出：1

提示：

• 1 <= strs.length <= 300
• 1 <= strs[i].length <= 300
• strs[i] 只包含小写字母。
• strs 中的所有单词都具有相同的长度，且是彼此的字母异位词。

解析

题目大意：给出一个字符串数组，要求找出这个数组中，“不相似”的字符串有多少种？

“相似字符串”的定义：

• 如果A和B字符串只需要交换一次字母的位置就能变成两个相等的字符串，那么A和B是相似的
• 即：A和B相似，有两种情况：

• • A == B
  • A和B只有两个字符不相等，其他字符都相等，这样交换一次才能完全相等

• 而且题目中说了，字符串数组是“字母异位词”，即字符的种类和个数都完全一样，只是顺序不同

那么，什么叫做“相似字符串组呢”？即相似字符串组中的每个字符串都有另外至少一个字符串和它相似。比如对于 {“tars”, “rats”, “arts”} 这个相似字符串组而言，相似关系是 “tars” <=> “rats” <=> “arts” 。

可以看到“相似字符串组之间的关系有传递性，对于这种群组分类问题，是并查集的经典应用场合：

• 我们可以将每个字符串看成是一个节点
• 如果两个字符串相似，就将它们merge
• 最后数有多少个联通分量即可。

怎么判断字符串A和字符串B是否相似呢？只要按位置对比字符，若不相等则 diff 自增1，若 diff 大于2了直接返回 false，因为只有 diff 正好等于2或者0的时候才相似。

这个题目作为hard 有点名不副实，理解清楚题意即可

PS： 这个题目有一个点比较关键，就是会存在重复的字符串，如果没有重复的字符串，就可以不用并查集，直接做一个compare函数做相似判断，然后O（N^2），做一次一一对比，求相似对就可以了；

但是因为有相似的数组，所以会出现重复记录的情况，因此需要利用并查集提前知道是否存在已经被记录的相同字符串。

代码

class Solution {
    class UnionFind{
    private:
        std::vector<int> parent_; // parent[i] = k ： i的父亲是k
        std::vector<int> size_;   // size[i] = k ： 如果i是代表节点，size[i]才有意义( i所在的集合大小是多少)，否则无意义
        std::vector<int> help_;  //  辅助结构
        int cnt_;               //一共有多少个集合

        int findRoot(int i){
            int hi = 0;
            while (i != parent_[i]){
                help_[hi++] = parent_[i];
                i = parent_[i];
            }
            for (hi--; hi >= 0; --hi) {
                parent_[help_[hi]] = i;
            }
            return i;
        }
    public:
        explicit UnionFind(int n){
            cnt_ = n;
            parent_.resize(n);
            size_.resize(n);
            help_.resize(n);
            for (int i = 0; i < n; ++i) {
                parent_[i] = i;
                size_[i] = 1;
            }
        }




        void merge(int i, int j){
            int f1 = findRoot(i);
            int f2 = findRoot(j);
            if(f1 != f2){
                if(size_[f1] >= size_[f2]){
                    parent_[f2] = f1;
                    size_[f1] = size_[f1] + size_[f2];
                }else{
                    parent_[f1] = f2;
                    size_[f2] = size_[f2] + size_[f1];
                }
                --cnt_;
            }
        }

        int counts() const{
            return cnt_;
        }

        bool isConnected(int i, int j){
            return findRoot(i) == findRoot(j);
        }
    };

public:
    int numSimilarGroups(vector<string>& strs) {
        int N = strs.size();
        UnionFind unionFind(N);
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                // 已经连接了，不用判断相似性
                if(unionFind.isConnected(i, j)){
                    continue;
                }

                if(isSimilar(strs[i], strs[j])){
                    unionFind.merge(i, j);
                }
            }
        }

        return unionFind.counts();
    }

private:
    bool isSimilar(const string& A,const string& B){
        int diff = 0;
        for(int i = 0; i < A.size(); i++){
            if(A[i] == B[i]){
                continue;
            }
            diff++;
        }
        return diff <= 2;
    }
};