[数据结构与算法]计算思维第3章 算法思维

前言回顾

? ? ? ? 冯·诺依曼计算机的构成包括：运算器；控制器；存储器；输入设备；输出设备；
? ? ? ? 程序计数器PC存储的是下一条机器指令的地址；
? ? ? ? 操作系统的资源管理主要包括：(外部)设备管理、处理机 (CPU) 管理、存储 (内存) 管理、文件 (磁盘) 管理；
? ? ? ? 在单CPU系统中，分时操作系统可以实现程序的并发执行。

目录

一、算法类问题求解框架

? ? ? ? 1.算法及特点

二、内排序

? ? ? ? 1.冒泡排序

? ? ? ? 2.二路归并排序

三、外排序

一、算法类问题求解框架

? ? ? ? 1.算法及特点

? ? ? ? 算法：描述求解问题方法的步骤集合
? ? ? ? 特点：确定性；可执行性；可终止性；有零个或多个输入；有一个或多个输入。

? ? ? ??算法类问题求解的一般步骤：
? ? ? ? 1.问题抽象及数学建模；2.算法策略设计；3.算法的数据结构和控制结构设计；
? ? ? ? 4.算法的实现；5.算法的分析。

二、内排序

? ? ? ? 内排序：所有待排序记录可以一次性装入内存中进行的排序。

? ? ? ? 1.冒泡排序

? ? ? ? 冒泡排序——穷举法，也称蛮力法，是一种基于遍历的方法。
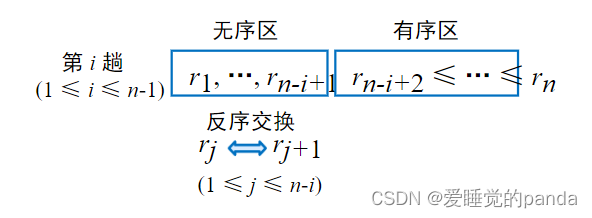
? ? ? ? 冒泡排序思想：

? ? ? ? 示例代码：

void BubbleSort(int r[],int n)//升序排序
{
    for(int i=0;i<n;i++){
        for(int j=i+1;j<n;j++){
            if(r[i]>r[j]){
                int temp = r[i];
                r[i] = r[j];
                r[j] = temp;
            }
    }
}

? ? ? ? 改进后的示例代码：

void BubbleSort_1(int r[],int n)//改进一，升序排序
{
    int exchange=1,i=1,j,temp;
    while(exchange){
        exchange=0;
        for(j=0;j<n-i;j++){
            if(r[j]>r[j+1]){
                temp = r[j];
                r[j] = r[j+1];
                r[j+1] = temp;
                exchange = 1;
            }
        }
        i++;
    } 
}

void BubbleSort_2(int r[],int n)//改进二，升序排序
{
    int exchange=n-1,bound=n-1,j,temp;
    while(exchange){
        exchange = 0;
        for(j=0;j<bound;j++){
            if(r[j]>r[j+1]){
                temp = r[j];
                r[j] = r[j+1];
                r[j+1] = temp;
                exchange = j;  
            }
        }
        bound = exchange;
    }
}

? ? ? ? 冒泡排序的分析
? ? ? ? 时间复杂性：
? ? ? ? ? ? ? ? 1.最坏情况：n(n-1)/2 = O(n^2);
? ? ? ? ? ? ? ? 2.最好情况：n-1 = O(n);

? ? ? ? ? ? ? ? 3.平均情况：O(n^2)。
? ? ? ? 空间复杂性：
? ? ? ? ? ? ? ? 1.输入空间：O(n)；
? ? ? ? ? ? ? ? 2.辅助空间：O(1)。

? ? ? ? 2.二路归并排序

? ? ? ? 算法思想——分治法：将一个难以直接解决的大规模原问题划分成k个可以直接解决的小规模子问题，分别求解各个子问题，再合并子问题解得到原问题解。

? ? ? ? 示例代码：

void MergeSort(int r[],int p[],int s,int e)//归并排序，升序排序
{
    int m;
    if(s == e) return;
    else{
        m = (s+e)/2;
        MergeSort(r,p,s,m);
        MergeSort(r,p,m+1,e);
        Merge(r,p,s,m,e);
    }   
}
void Merge(int r[],int p[],int s,int m,int e)//归并，升序
{
    int i,j,k;
    i = s;
    while(i<=m) p[i] = r[i++];
    i = sl
    j = m+1;
    k = s;
    while(i<=m && j<=e){
        if(p[i]<=r[j]) r[k++] = p[i++];
        else r[k++] = r[j++];
    }
    while(i<=m) r[k++] = p[i++];
}

? ? ? ? 二路归并排序的分析
? ? ? ? 时间复杂性：
? ? ? ? ? ? ? ? 1.最坏情况：O(nlogn);

? ? ? ? ? ? ? ? 2.最好情况：O(nlogn);
? ? ? ? ? ? ? ? 3.最坏情况：O(nlogn);

? ? ? ? 空间复杂性：

? ? ? ? ? ? ? ? 1.输入空间：O(n);

? ? ? ? ? ? ? ? 2.辅助空间：O(n);

三、外排序

? ? ? ? 外排序的基本算法思想：排序-归并。
? ? ? ? 排序-归并——分治法：第一阶段，排序，根据可用内存，将外存的记录分成若干段，将每段依次读入内存并利用内排序进行排序，再将排序后每段写入外存。排序后的有序段称为归并段。第二阶段，归并，根据可用内存，将归并段依次读入内存，进行归并，再写入外存，逐渐得到更大的归并段，直至得到所有记录的归并段即有序段。
? ? ? 对同一文件进行“排序-归并”外排序时，读/写外存次数与归并趟数成正比，我们可以通过增加归并的个数，即多路归并来减少归并趟数。但在减少归并趟数的同时，内部归并的时间将增加。那我们不能简单地内部归并排序，于是我们引入了败者树。