数据结构

数组模拟栈

int stk[N], tt;
//插入
stk[++tt] = x;
//弹出
tt --;
//判断是否为空
if(tt>0) not empty;
else empty;
//取栈顶元素
stk[tt];

队列

int q[N], hh , tt = -1;//hh对头，tt队尾
//插入
q[++tt] = x;//在队尾插入元素
hh++; //在对头弹出元素

if(hh<=tt) not empty;
else empty;

q[hh]//取队头元素
q[tt]//取队尾元素

单调栈：

如：找出 $i$ 左边比他第一个小的数

假如存在 $x<y, a_x ≥ a_y`$ 的话，则可以把 $a_x$ 删掉。剩下的点就是一个严格单调上升的序列了。

如果栈顶大于 $a_i$ ，那么栈顶元素就可以被删掉。一直删，直到找到一个元素满足 $stk[tt]<a_i$ 。然后把 $a_i$ 插到栈里。
```
int n;
int stk[N],tt;
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		int x;
		cin>>x;
		while(tt && stk[tt] >= x) tt--;//栈不空，且栈顶元素大于当前元素，说明栈顶永远用不到了，出栈
		if(tt) cout<<stk[tt]<<" ";//栈非空，找到了符合的
		else cout<<-1<<' ';//不存在

		stk[tt++]=x;
	}
	return 0;
}
```
看似两重循环，但是从tt我们可以看出，每个元素最多进栈出栈一次，所以是0(n)

单调队列

如：输出滑动窗口里的min。一般都是先考虑暴力O(nk)的复杂度，从中发现一些特性规律，降低时间复杂度。（看一下队列中的元素有没有没有用的，若存在，删除后看是否可以得到单调的序列。若可，最值，取两端点；中间值，考虑二分等）

同理，把逆序的点删掉取队头即可。

多重背包也能用单调队列优化。

int n,k;
int a[N],q[N];

int main(){
	scanf("%d%d",&n,&k);
	for(int i=0;i<n;i++） scanf("%d",&a[i]);
	
	int hh=0,tt=-1;
	for(int i=0;i<n;i++){
		//判断队头是否已经滑出窗口
		if(hh<=tt && i-k+1>q[hh]) hh++;
		while(hh<=tt &&a[q[tt]]>=a[i]) tt--;
		q[++tt]=i;//因为i也可能是最小值，所以要先入队，再输出
		if(i>=k-1) printf("%d ",a[q[hh]]);//题目要求输出前k个
	}
  puts("");

	//最大的仅仅需要改变一个符号。得到的是单减序列，最大值也是队头
	hh=0,tt=-1;
	for(int i=0;i<n;i++){
		//判断队头是否已经滑出窗口
		if(hh<=tt && i-k+1>q[hh]) hh++;//采用if的原因是因为该题只有一次；不确定多少次的话用while
		while(hh<=tt &&a[q[tt]] <= a[i]) tt--;
		q[++tt]=i;//因为i也可能是最小值，所以要先入队，再输出
		if(i>=k-1) printf("%d ",a[q[hh]]);//题目要求输出前k个
	}
  puts("");
	return 0;
}

KMP

相等的前缀和后缀最大是多少

以i为终点的后缀和从1开始的前缀。next[i]=j意味着 p[1,…,j]=p[i-j+1,…,i]
Trie树：高效地存储和查找字符串集合的数据结构；

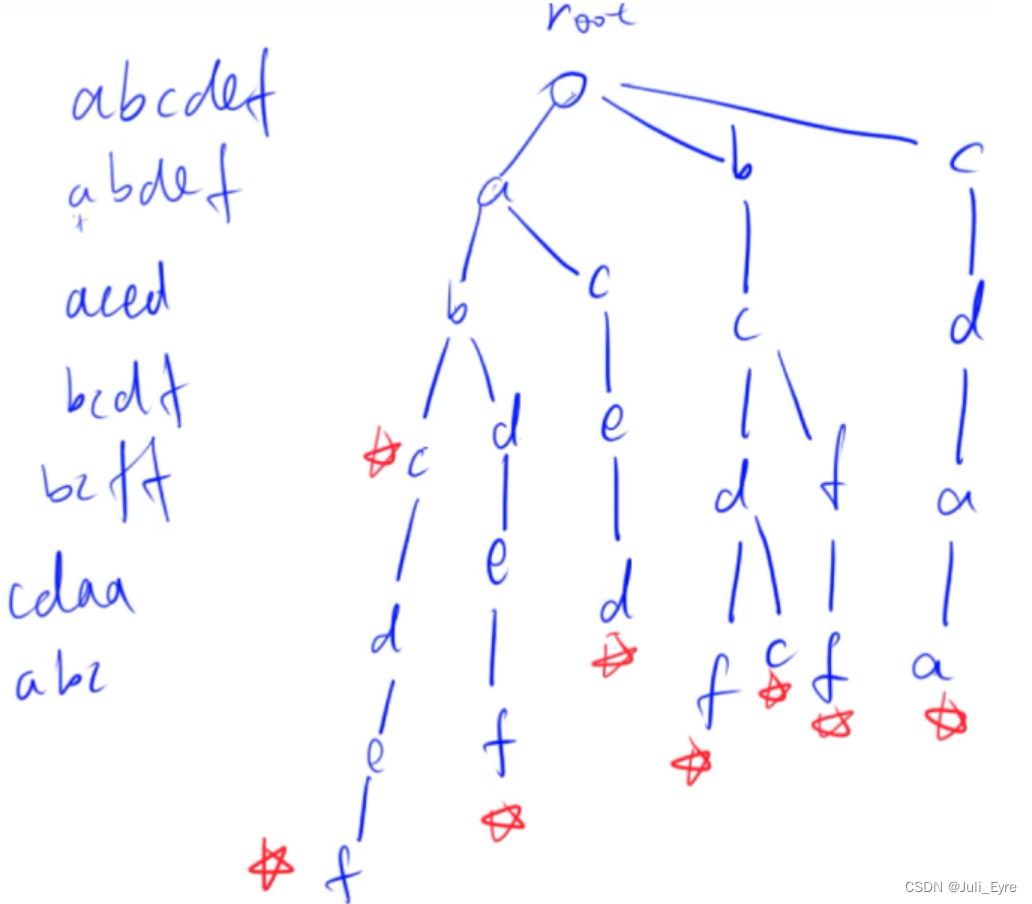
在这里插入图片描述

```cpp
int son[N][26];//因为每个节点最多和26个英文字母相连
int cnt[N],idx;//cnt存的是以当前这个点结尾的单词有多少个，idx是当前用到了哪个下标与单链表中相同
//下标是0的点，既是根节点又是空结点，若一个节点没有子节点，我们也会把他指向根节点

void insert(char str[]){
	int p=0;
	for(int i=0;str[i];i++){
		int u=str[i]-'a';//映射到0-25
		if(!son[p][u]) son[p][u] = ++ idx;//如果结点p不存在u这个儿子的话，则创建出来
		p = son[p][u];//继续往下走
	}
	cnt[p]++;//以p结尾的单词数++
}

int query(char str[]){//返回字符串出现多少次
	int p=0;
	for(int i=0;str[i];i++){
		int u = str[i]-'a';
		if(!son[p][u]) return 0;//不存在该字符
		p = son[p][u];
	}
	return cnt[p];
}
```

并查集

在近乎O(1)的复杂度内，将两个集合合并/询问两个元素是否在一个集合当中

每个集合用一颗树来表示，根节点是集合的代表元素，根节点的编号是集合的编号；每个点都要存储他的父节点是谁。（用p[x]表示父节点）

问题1：如何判断树根：

if (p[x]==x) 是树根

问题2：如何求x的集合编号：

while(p[x]!= x) x = p[x];//不是树根，就一直往上走

问题3：如何合并两个集合：

假设px是x的集合编号，py是y的集合编号。则p[px] = py

优化：压缩路径。 前面不优化的还是取决于树的高度的

找到根节点后，直接把路径上的所有点都指向根节点

int p[N], sizep[N]//size代表每个集合中有几个点
**int find(int x){//返回x的祖宗节点+路径压缩
	if(p[x] != x) p[x]=find(p[x]);//如果x不是根节点的话
	return p[x];//回溯的时候直接是压缩路径
}**

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) p[i]=i,size[i]=1;//初始化
	
	while(m--){
		char op[2];
		int a,b;
		scanf("%s%d%d",op,&a,&b);
		
		if(op[0] == 'M')  p[find(a)] = find(b);//合并
		//某一个点所在集合中点的数量
		//假设只有根节点的size是有意义的
		if(find(a) == find(b)) continue;//如果ab已经在同一个集合里了，就不需任何操作了
		size[find(b)] += size[find(a)],p[find(a)] = find(b),printf("%d\n",size[find(a)]);

如何用并查集数集合中的数量

连通块中点的数量

连通块：如果从a可以走到b，b也可以走到a的话，就说明a和b在同一个连通块中

堆（STL中的堆是一个优先队列）

op：插入一个数，求集合中的最小值；删除最小值；删除任意一个元素；修改任意一个元素

堆是一个完全二叉树；小根堆：根节点≤左右节点

使用一维数组进行存储（完全二叉树也是这样存的。(从1开始的)

结点x	x的左儿子：2x	x的右儿子：2x+1

插入一个数：在整个堆的最后一个位置插入一个元素，在不断往上移。

heap[++ size] = x;up(size);
heap[1];//求集合中的最小值

//删除最小值(头部节点)：
//用最后一个元素覆盖掉堆顶元素，size--，删掉最后一个元素 down(1);
heap[1]=heap[size];size--;down(1)//让1号点往下走

//删除任意一个元素k
heap[k]=heap[size];size--;down(k);up(k);//down和up只会执行一个；若heap[k]变大了，则down

//修改元素
heap[k]=x;down(k);up(k);
//求最小值O(1)，插入删除O(logn)

若下标从0开始，则左儿子是2x还是0，冲突了

void down(int u){
	int t = u;
	if(u*2<size && h[u*2]<h[t]) t=u*2;//左儿子存在并且小
	if(u*2+1<=size && h[u*2+1]<h[t]) t=u*2+1;
	if(u != t)//需要交换，即t不是父节点了
	{
			swap(h[u],h[t]);
			down(t);//交换后的位置是否合适，还要继续判断
	}
}

//堆的初始化
for(int i=1;i<=n;i++) scanf("%d",&h[i]);
size=n;
for(int i=n/2;i;i--) down(i);//以O(n)的方式建堆，插入n个结点的话是O(nlogn)
// n/2那层最多降1层，n/4那层最多降2层，n/8那层最多降3层
//从n/2开始，是因为最后一半元素一定是堆，因为只有一个数，然后归纳证明。假设最下面一层都是堆了，依次往上down,满足了堆顶最小的条件
//因此，整个也就是一个堆了

哈希：（离散化是一种特殊的哈希方式，离散化需要单增）

一般直接取模 (x%N+N)%N 即可，模要取一个质数，不容易冲突。一般情况时间复杂度为O(1)
- 存储结构：开放地址法/拉链法
  - 拉链法：一维数组+链表
  - 开放地址法：仅需一维数组，长度通常需要输入数目的2-3倍；
    
    思路：从前往后，直到找到第一个空的坑位再插进去；删除也是先查找，用一个标记实现的
```
const int null = 0x3f3f3f3f;
//后面main memset(h,0x3f,sizeof h); memset是按照字节进行的，不能处理vector

int find(int x){
	int k = (x%N+N)%N;
	while(h[k] != null [//h[k]!=null说明这个位置上有人
		k++;
		if(k == N)  k = 0;//找完一轮了，从头开始
	}
	return k;
}//不在，k就是x应该存储的位置；在哈希表中，k就是x的下标
```
- 字符串前缀哈希法：（可以计算出任意一个字串的哈希值）
  
  先预处理出来每个前缀的哈希值
  
  从L到R的字串的哈希值： $h[R]-h[L-1]*P^{R-L+1}$