14天阅读挑战赛
努力是为了不平庸~
算法学习有些时候是枯燥的,这一次,让我们先人一步,趣学算法!欢迎记录下你的那些努力时刻(算法学习知识点/算法题解/遇到的算法bug/等等),在分享的同时加深对于算法的理解,同时吸收他人的奇思妙想,一起见证技术er的成长~
一、动态规划
动态规划也是一种分治思想,但与分治算法不同的是,分治算法是把原问题分解为若干子问题,自顶向下求解各子问题,合并子问题的解,从而得到原问题的解。动态规划也是把原问题分解为若干子问题,然后自底向上,先求解最小的子问题,把结果存储在表格中,再求解大的子问题时,直接从表格中查询小的子问题的解,避免重复计算,从而提高算法效率。
1.使用动态规划需要满足的性质:
(1)最优子结构。最优子结构性质是指问题的最优解包含其子问题的最优解。
(2)子问题重叠。子问题重叠是指在求解子问题的过程中,有大量的子问题是重复的。
(3)无后效性。当前阶段的求解只和前面阶段有关,和后续阶段无关,称为“无后效性”。
2.动态规划解决问题的步骤:
(1)分析最优解的结构特征。
(2)建立最优值的递归式。
(3)自底向上计算最优值,并记录。
(4)构造最优解。
二、动态规划算法实例——最长公共子序列
1.问题描述
最长公共子序列问题是指:给定两个序列 X = X= X={ x 1 , x 2 , x 3 , … , x m x_1,x_2,x_3,…,x_m x1?,x2?,x3?,…,xm?}和 Y = Y= Y={ y 1 , y 2 , y 3 , … , y n y_1,y_2,y_3,…,y_n y1?,y2?,y3?,…,yn?},找出X和Y的一个最长的公共子序列。
2.问题分析
(1)分析最优解的结构特征
假设已经知道
Z
k
=
Z_k=
Zk?={
z
1
,
z
2
,
z
3
,
…
,
z
k
z_1,z_2,z_3,…,z_k
z1?,z2?,z3?,…,zk?}是
X
=
X=
X={
x
1
,
x
2
,
x
3
,
…
,
x
m
x_1,x_2,x_3,…,x_m
x1?,x2?,x3?,…,xm?}和
Y
=
Y=
Y={
y
1
,
y
2
,
y
3
,
…
,
y
n
y_1,y_2,y_3,…,y_n
y1?,y2?,y3?,…,yn?}的最长公共子序列。
-
x m = y n = z k x_m=y_n=z_k xm?=yn?=zk?,那么 Z k ? 1 = Z_{k-1}= Zk?1?={ z 1 , z 2 , z 3 , … , z k ? 1 z_1,z_2,z_3,…,z_{k-1} z1?,z2?,z3?,…,zk?1?}是 X m ? 1 X_{m-1} Xm?1?和 Y n ? 1 Y_{n-1} Yn?1?的最长公共子序列。

-
x m ≠ y n x_m≠y_n xm?=yn?, x m ≠ z k x_m≠z_k xm?=zk?。可以把 x m x_m xm?去掉,那么 Z k Z_k Zk?是 X m ? 1 X_{m-1} Xm?1?和 Y n Y_n Yn?的最长公共子序列。

-
x m ≠ y n x_m≠y_n xm?=yn?, y n ≠ z k y_n≠z_k yn?=zk?。可以把 y n y_n yn?去掉,那么 Z k Z_k Zk?是 X m X_m Xm?和 Y n ? 1 Y_{n-1} Yn?1?的最长公共子序列。

(2)建立最优值的递归式
设
c
[
i
]
[
j
]
c[i][j]
c[i][j]表示
X
i
X_i
Xi?和
Y
j
Y_j
Yj?的最长公共子序列长度。
?
x
m
=
y
n
=
z
k
:
x_m= y_n= z_k:
xm?=yn?=zk?:那么
c
[
i
]
[
j
]
=
c
[
i
?
1
]
[
j
?
1
]
+
1
;
c[i][j]= c[i?1][j?1]+1;
c[i][j]=c[i?1][j?1]+1;
?
x
m
≠
y
n
:
x_m≠y_n:
xm?=yn?:那么只需要求解
X
i
X_i
Xi?和
Y
j
?
1
Y_{j?1}
Yj?1?的最长公共子序列和
X
i
?
1
X_{i?1}
Xi?1?和
Y
j
Y_j
Yj?的最长公共子序列,取最大值:
c
[
i
]
[
j
]
=
m
a
x
c[i][j]= max
c[i][j]=max{
c
[
i
]
[
j
?
1
]
,
c
[
i
?
1
]
[
j
]
c[i][j?1], c[i?1][j]
c[i][j?1],c[i?1][j]}。
c
[
i
]
[
j
]
=
{
0
,
i
=
0
或
j
=
0
c
[
i
?
1
]
[
j
?
1
]
+
1
,
i
,
j
>
0
且
x
i
=
y
j
m
a
x
{
c
[
i
]
[
j
?
1
]
,
c
[
i
?
1
]
[
j
]
}
,
i
,
j
>
0
且
x
i
≠
y
j
c[i][j]= \begin{cases} 0& \text{$,i=0或j=0$}\\ c[i-1][j-1]+1& \text{$,i,j>0且x_i=y_j$}\\ max\{c[i][j-1],c[i-1][j]\}& \text{$,i,j>0且x_i≠y_j$} \end{cases}
c[i][j]=?
?
??0c[i?1][j?1]+1max{c[i][j?1],c[i?1][j]}?,i=0或j=0,i,j>0且xi?=yj?,i,j>0且xi?=yj??
(3)自底向上计算最优值,并记录最优值和最优策略
i
=
1
i=1
i=1时:
{
x
1
}
\{x_1\}
{x1?}和
{
y
1
,
y
2
,
y
3
,
…
,
y
n
}
\{y_1,y_2,y_3,…,y_n\}
{y1?,y2?,y3?,…,yn?}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
i
=
2
i=2
i=2时:
{
x
2
}
\{x_2\}
{x2?}和
{
y
1
,
y
2
,
y
3
,
…
,
y
n
}
\{y_1,y_2,y_3,…,y_n\}
{y1?,y2?,y3?,…,yn?}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
··········
(4)构造最优解
c
[
i
]
[
j
]
c[i][j]
c[i][j]的来源一共有3个:
c
[
i
]
[
j
]
=
c
[
i
?
1
]
[
j
?
1
]
+
1
,
c
[
i
]
[
j
]
=
c
[
i
]
[
j
?
1
]
,
c
[
i
]
[
j
]
=
c
[
i
?
1
]
[
j
]
c[i][j]= c[i?1][j?1]+1, c[i][j]= c[i][j?1],c[i][j]= c[i?1][j]
c[i][j]=c[i?1][j?1]+1,c[i][j]=c[i][j?1],c[i][j]=c[i?1][j]。计算最优值时,用辅助数组
b
[
i
]
[
j
]
b[i][j]
b[i][j]记录来源:
c
[
i
]
[
j
]
=
c
[
i
?
1
]
[
j
?
1
]
+
1
,
b
[
i
]
[
j
]
=
1
;
c[i][j]= c[i?1][j?1]+ 1, b[i][j] =1;
c[i][j]=c[i?1][j?1]+1,b[i][j]=1;
c
[
i
]
[
j
]
=
c
[
i
]
[
j
?
1
]
,
b
[
i
]
[
j
]
=
2
;
c[i][j]= c[i][j?1] , b[i][j] =2;
c[i][j]=c[i][j?1],b[i][j]=2;
c
[
i
]
[
j
]
=
c
[
i
?
1
]
[
j
]
,
b
[
i
]
[
j
]
=
3
。
c[i][j]= c[i?1][j] , b[i][j] =3。
c[i][j]=c[i?1][j],b[i][j]=3。
这样就可以根据
b
[
m
]
[
n
]
b[m][n]
b[m][n]反向追踪最长公共子序列,当
b
[
i
]
[
j
]
=
1
b[i][j] =1
b[i][j]=1时,输出
x
i
x_i
xi?;当
b
[
i
]
[
j
]
=
2
b[i][j] =2
b[i][j]=2时,追踪
c
[
i
]
[
j
?
1
]
c[i][j?1]
c[i][j?1];当
b
[
i
]
[
j
]
=
3
b[i][j] =3
b[i][j]=3时,追踪
c
[
i
?
1
]
[
j
]
c[i?1][j]
c[i?1][j] ,直到
i
=
0
i=0
i=0或
j
=
0
j=0
j=0停止。
3.程序代码
//最长公共子序列
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1005;
int c[maxn][maxn],m,n,b[maxn][maxn];//b[][]记录最优值来源
char s1[maxn],s2[maxn];
void LCS(){
memset(c,0,sizeof(c));
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(s1[i-1]==s2[j-1]){
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
else if(c[i][j-1]>=c[i-1][j]){//两者找最大值,并记录最优值来源
c[i][j]=c[i][j-1];
b[i][j]=2;
}
else{
c[i][j]=c[i-1][j];
b[i][j]=3;
}
}
}
}
void print(int i,int j){//根据b[i][j]构造最长公共子序列
if(i==0||j==0) return;
if(b[i][j]==1){
print(i-1,j-1);
printf("%c",s1[i-1]);
}
else if(b[i][j]==2)
print(i,j-1);
else
print(i-1,j);
}
int main(){
int t;//测试用例数
scanf("%d",&t);
while(t--){
scanf("%s",s1);
scanf("%s",s2);
m=strlen(s1);
n=strlen(s2);
LCS();
printf("%d\n",c[m][n]);
print(m,n);
}
return 0;
}
4.算法复杂度分析
(1)时间复杂度:由于每个数组单元的计算耗费
O
(
1
)
Ο(1)
O(1)时间,如果两个字符串的长度分别是m、n,那么算法时间复杂度为
O
(
m
n
)
Ο(mn)
O(mn)。
(2)空间复杂度:空间复杂度主要为两个二维数组
c
[
]
[
]
,
b
[
]
[
]
c[][],b[][]
c[][],b[][],占用的空间为
O
(
m
n
)
O(mn)
O(mn)。
三、动态规划算法实例——矩阵连乘
1.问题描述
给定n个矩阵 { A 1 , A 2 , A 3 , … , A n } \{A_1,A_2,A_3,…,A_n\} {A1?,A2?,A3?,…,An?},其中, A i A_i Ai?和 A i + 1 ( i = 1 , 2 , … , n ? 1 ) A_{i+1}(i=1,2,…,n?1) Ai+1?(i=1,2,…,n?1)是可乘的。用加括号的方法表示矩阵连乘的次序,不同的计算次序计算量(乘法次数)是不同的,找出一种加括号的方法,使得矩阵连乘的计算量最小。
2.问题分析
(1)什么是矩阵可乘?
如果两个矩阵,第1个矩阵的列等于第2个矩阵的行时,那么这两个矩阵是可乘的。

(2)矩阵相乘后的结果是什么?
多个矩阵相乘的结果矩阵,其行、列分别等于第1个矩阵的行、最后一个矩阵的列。

无论矩阵的计算次序如何都不影响结果矩阵。
(3)两个矩阵相乘需要多少次乘法?
A
m
×
n
、
A
n
×
k
A_{m×n}、A_{n×k}
Am×n?、An×k?相乘执行乘法运算的次数为
m
×
n
×
k
m×n×k
m×n×k。
3.算法设计
下面分析矩阵连乘问题
A
i
A
i
+
1
…
A
j
A_iA_{i+1}…A_j
Ai?Ai+1?…Aj?是否具有最优子结构性质。
(1)分析最优解的结构特征
假设我们已经知道了在第k个位置加括号会得到最优解,那么原问题就变成了两个子问题:
(
A
i
A
i
+
1
…
A
k
),(
A
k
+
1
A
k
+
2
…
A
j
)
(A_iA_{i+1}…A_k),(A_{k+1}A_{k+2}…A_j)
(Ai?Ai+1?…Ak?),(Ak+1?Ak+2?…Aj?)
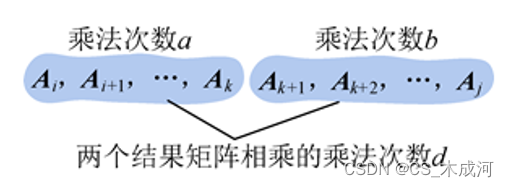
假设 A i A i + 1 … A j A_iA_{i+1}…A_j Ai?Ai+1?…Aj?的乘法次数是c,那么 c = a + b + d c=a+b+d c=a+b+d,结果矩阵的乘法次数d不变。只需要证明如果c是最优的,则a和b一定是最优的。
(2)建立最优值递归式
用
m
[
i
]
[
j
]
m[i][j]
m[i][j]表示
A
i
A
i
+
1
…
A
j
A_iA_{i+1}…A_j
Ai?Ai+1?…Aj?矩阵连乘的最优值,那么两个子问题
(
A
i
A
i
+
1
…
A
k
)、(
A
k
+
1
A
k
+
2
…
A
j
)
(A_iA_{i+1}…A_k)、(A_{k+1}A_{k+2}…A_j)
(Ai?Ai+1?…Ak?)、(Ak+1?Ak+2?…Aj?)对应的最优值分别是
m
[
i
]
[
k
]
、
m
[
k
+
1
]
[
j
]
m[i][k]、m[k+1][j]
m[i][k]、m[k+1][j]。只需考查结果矩阵相乘的乘法次数。
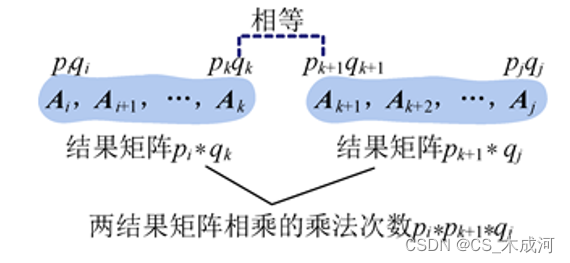
如果用一维数组p[]来记录矩阵的行和列,第i个矩阵的行数存储在数组的第i?1位置,列数存储在数组的第i位置,那么
p
i
?
p
k
+
1
?
q
j
p_i*p_{k+1}*q_j
pi??pk+1??qj?对应的数组元素相乘为
p
[
i
?
1
]
?
p
[
k
]
?
p
[
j
]
p[i?1]*p[k]* p[j]
p[i?1]?p[k]?p[j],原递归式变为:
m
[
i
]
[
j
]
=
{
0
,
i
=
j
m
i
n
i
≤
k
<
j
{
m
[
i
]
[
k
]
+
m
[
k
+
1
]
[
j
]
+
p
[
i
?
1
]
?
p
[
k
]
?
p
[
j
]
}
,
i
<
j
m[i][j]= \begin{cases} 0& \text{$,i=j$}\\ \underset{i≤k<j}{min}\{m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]\}& \text{$,i<j$} \end{cases}
m[i][j]=?
?
??0i≤k<jmin?{m[i][k]+m[k+1][j]+p[i?1]?p[k]?p[j]}?,i=j,i<j?
(3)自底向上计算并记录最优值
先求两个矩阵相乘的最优值,再求3个矩阵相乘的最优值,直到n个矩阵连乘的最优值。
(4)构造最优解
上面得到的最优值只是矩阵连乘的最小的乘法次数,并不知道加括号的次序,需要从记录表中还原加括号次序,构造最优解。
4.程序代码
//矩阵连乘
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=105;
const int inf=0x3f3f3f3f;
int p[maxn],m[maxn][maxn],s[maxn][maxn];
int matrixchain(int n){ //求最优值
memset(m,0,sizeof(m));
memset(s,0,sizeof(s));
for(int d=2;d<=n;d++){ //问题规模d
for(int i=1;i<=n-d+1;i++){ //区间起点
int j=i+d-1; //区间终点
m[i][j]=inf; //初始化为无穷大,后面需要找最小值
for(int k=i;k<j;k++){ //枚举从i到j-1的所有决策,求最优值,记录最优策略
int temp=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(temp<m[i][j]){
m[i][j]=temp;
s[i][j]=k;
}
}
}
}
return m[1][n];
}
void print(int i,int j){ //构造最优解
if(i==j){
cout<<"A["<<i<<"]";
return ;
}
cout<<"(";
print(i,s[i][j]);
print(s[i][j]+1,j);
cout<<")";
}
int main(){
int t,n; //测试用例数,矩阵个数
cin>>t;
while(t--){
cin>>n;
for(int i=0;i<=n;i++)
cin>>p[i];
cout<<matrixchain(n)<<endl;
//print(1,n);
//cout<<endl;
}
return 0;
}
5.算法复杂度分析
(1)时间复杂度:语句
t
=
m
[
i
]
[
k
]
+
m
[
k
+
1
]
[
j
]
+
p
[
i
?
1
]
?
p
[
k
]
?
p
[
j
]
t= m[i][k] + m[k+1][j] +p[i?1]*p[k]*p[j]
t=m[i][k]+m[k+1][j]+p[i?1]?p[k]?p[j],在3层for循环中嵌套,该语句的执行次数为
O
(
n
3
)
O(n^3)
O(n3),时间复杂度为
O
(
n
3
)
O(n^3)
O(n3)。
(2)空间复杂度:该程序的输入数据的数组为
p
[
]
p[]
p[],辅助数组
m
[
]
[
]
、
s
[
]
[
]
m[][]、s[][]
m[][]、s[][],因此空间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
四、动态规划算法实例——01背包
1.问题描述
假设有n个物品和1个购物车,每个物品i对应价值为 v i v_i vi?,重量 w i w_i wi?,购物车的容量为W(也可以将重量设定为体积)。每个物品只有1件,要么装入,要么不装入,不可拆分。在购物车不超重的情况下,如何选取物品装入购物车,使所装入的物品的总价值最大?最大价值是多少?装入了哪些物品?
2.问题分析
有n个物品和购物车的容量,每个物品的重量为
w
[
i
]
w[i]
w[i],价值为
v
[
i
]
v[i]
v[i],购物车的容量为W。选若干个物品放入购物车,使价值最大,可表示如下。
约束条件:
{
∑
i
=
1
n
w
i
x
i
≤
W
x
i
∈
{
0
,
1
}
,
1
≤
i
≤
n
约束条件: \begin{cases} \sum_{i=1}^{n} w_ix_i≤W\\ x_i∈\{0,1\}& \text{$,1≤i≤n$} \end{cases}
约束条件:{∑i=1n?wi?xi?≤Wxi?∈{0,1}?,1≤i≤n?
目标函数:
m
a
x
∑
i
=
1
n
v
i
x
i
目标函数:max\sum_{i=1}^{n}v_ix_i
目标函数:maxi=1∑n?vi?xi?
问题归结为求解满足约束条件,使目标函数达到最大值的解向量
X
=
{
x
1
,
x
2
,
…
,
x
n
}
X=\{x_1,x_2,…,x_n\}
X={x1?,x2?,…,xn?}。
(1)分析最优解的结构特征
假设已经知道了
X
=
{
x
1
,
x
2
,
…
,
x
n
}
X=\{x_1,x_2,…,x_n\}
X={x1?,x2?,…,xn?}是原问题
{
a
1
,
a
2
,
…
,
a
n
}
\{a_1,a_2,…,a_n\}
{a1?,a2?,…,an?}的最优解,那么原问题去掉第一个物品就变成了子问题
{
a
2
,
a
3
,
…
,
a
n
}
\{a_2,a_3,…,a_n\}
{a2?,a3?,…,an?}。

子问题的约束条件和目标函数如下:
约束条件:
{
∑
i
=
2
n
w
i
x
i
≤
W
?
w
1
x
1
x
i
∈
{
0
,
1
}
,
2
≤
i
≤
n
约束条件: \begin{cases} \sum_{i=2}^{n} w_ix_i≤W-w_1x_1\\ x_i∈\{0,1\}& \text{$,2≤i≤n$} \end{cases}
约束条件:{∑i=2n?wi?xi?≤W?w1?x1?xi?∈{0,1}?,2≤i≤n?
目标函数:
m
a
x
∑
i
=
2
n
v
i
x
i
目标函数:max\sum_{i=2}^{n}v_ix_i
目标函数:maxi=2∑n?vi?xi?
只需要证明:
X
′
=
{
x
2
,
…
,
x
n
}
X'=\{x_2,…,x_n\}
X′={x2?,…,xn?}是子问题
{
a
2
,
…
,
a
n
}
\{a_2,…,a_n\}
{a2?,…,an?}的最优解,即证明最优子结构性质。
(2)建立最优值的递归式
对每个物品依次检查是否放入或者不放入:
用
c
[
i
]
[
j
]
c[i][j]
c[i][j]表示前i件物品放入容量为j的购物车可以获得的最大价值。
? 不放入第
i
i
i件物品,
x
i
=
0
x_i=0
xi?=0,装入购物车的价值不增加。问题就转化为“前
i
?
1
i?1
i?1件物品放入容量为
j
j
j的背包中”,最大价值为
c
[
i
?
1
]
[
j
]
c[i?1][j]
c[i?1][j]。
? 放入第
i
i
i件物品,
x
i
=
1
x_i=1
xi?=1,装入购物车的价值增加
v
i
v_i
vi?。问题转化为“前
i
?
1
i?1
i?1件物品放入容量为
j
?
w
[
i
]
j?w[i]
j?w[i]的购物车中”,获得的最大价值
c
[
i
?
1
]
[
j
?
w
[
i
]
]
c[i?1][j?w[i]]
c[i?1][j?w[i]],再加上放入第
i
i
i件物品获得的价值
v
[
i
]
v[i]
v[i]。即
c
[
i
?
1
]
[
j
?
w
[
i
]
]
+
v
[
i
]
c[i?1][j?w[i]]+ v[i]
c[i?1][j?w[i]]+v[i]。
购物车容量不足,肯定不能放入;购物车容量足,我们要看放入、不放入哪种情况获得的价值更大。
递归式:
c
[
i
]
[
j
]
=
{
c
[
i
?
1
]
[
j
]
,
j
<
w
i
m
a
x
{
c
[
i
?
1
]
[
j
]
,
c
[
i
?
1
]
[
j
?
w
[
i
]
]
+
v
[
i
]
}
,
j
≥
w
i
c[i][j]= \begin{cases} c[i-1][j]& \text{$,j<w_i$}\\ max\{c[i-1][j],c[i-1][j-w[i]]+v[i]\}& \text{$,j≥w_i$} \end{cases}
c[i][j]={c[i?1][j]max{c[i?1][j],c[i?1][j?w[i]]+v[i]}?,j<wi?,j≥wi??
(3)循环阶段
· 按照递归式计算第1个物品的处理情况,得到
c
[
1
]
[
j
]
,
j
=
1
,
2
,
…
,
W
c[1][j],j=1,2,…,W
c[1][j],j=1,2,…,W。
· 按照递归式计算第2个物品的处理情况,得到
c
[
2
]
[
j
]
,
j
=
1
,
2
,
…
,
W
c[2][j],j=1,2,…,W
c[2][j],j=1,2,…,W。
· ……
· 按照递归式计算第n个物品的处理情况,得到
c
[
n
]
[
j
]
,
j
=
1
,
2
,
…
,
W
c[n][j],j=1,2,…,W
c[n][j],j=1,2,…,W。
(4)构造最优解
c
[
n
]
[
W
]
c[n][W]
c[n][W]就是不超过购物车容量能放入物品的最大价值。根据
c
[
]
[
]
c[][]
c[][]数组逆向构造最优解可以知道具体放入了哪些物品。
3.程序代码
//01背包
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=105;
const int maxw=10005;
int c[maxn][maxw];//c[i][j]表示前i个物品放入容量为j的背包获得的最大价值
int w[maxn],v[maxn];//w[i]表示第i个物品的重量,v[i]表示第i个物品的价值
bool x[maxn]; //x[i]表示第i个物品是否放入背包
int knapsack(int n,int W){
for(int i=1;i<=n;i++){//计算c[i][j]
for(int j=1;j<=W;j++){
if(j<w[i]) //当物品的重量大于背包的容量,则不放此物品
c[i][j]=c[i-1][j];
else //否则比较此物品放与不放哪种情况使得背包内的价值最大
c[i][j]=max(c[i-1][j],c[i-1][j-w[i]]+v[i]);
}
}
return c[n][W];
}
void print(int n,int W){//逆向构造最优解
int j=W;
for(int i=n;i>0;i--){
if(c[i][j]>c[i-1][j]){
x[i]=1;
j-=w[i];
}
else
x[i]=0;
}
cout<<"装入背包的物品序号为:";
for(int i=1;i<=n;i++){
if(x[i])
cout<<i<<" ";
}
cout<<endl;
}
int main(){
int n,W,t;//n表示n个物品,W表示背包的容量,t表示测试用例数
cin>>t;
while(t--){
cin>>n>>W;
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=n;i++)//初始化第0列为0
c[i][0]=0;
for(int j=1;j<=W;j++)//初始化第0行为0
c[0][j]=0;
cout<<knapsack(n,W)<<endl;
//print(n,W);
}
return 0;
}
4.算法复杂度分析
(1)时间复杂度:有两层嵌套的for循环,时间复杂度为
O
(
n
W
)
O(nW)
O(nW)。
(2)空间复杂度:二维辅助数组
c
[
n
]
[
W
]
c[n][W]
c[n][W],空间复杂度为
O
(
n
W
)
O(nW)
O(nW)。