十大算法
学完数据结构该学什么?当然是来巩固算法,下面介绍了十中比较常用的算法,希望能帮到大家。
包括:非递归二分查找、分治法、动态规划、贪心算法、回溯算法(骑士周游为例)、KMP、最小生成树算法:Prim、Kruskal、最短路径算法:Dijkstra、Floyd。
1.非递归二分查找
- 前面我们讲过了二分查找算法,是使用递归的方式,下面我们讲解二分查找算法的非递归方式
- 二分查找法只适用于从有序的数列中进行查找(比如数字和字母等),将数列排序后再进行查找
- 二分查找法的运行时间为对数时间o(logzn),即查找到需要的目标位置最多只需要logzn步,假设从[0,99]的队列(100个数,即n=100)中寻到目标数30,则需要查找步数为log2100,即最多需要查找7次(26<100<27)
package com.DataStructure;
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {1,3,5,7,9,10,15,88,999};
// 递归版 二分查找
System.out.println(binarySearchRecursion(arr,0,arr.length-1,88));
// 非递版 二分查找
System.out.println(binarySearch(arr,88));
}
public static int binarySearchRecursion(int[] arr,int head,int tail,int num) {
if (head>=tail) return -1;
int middle = (head+tail)/2;
if (arr[middle]==num) return middle;
else if (middle>num) return binarySearchRecursion(arr,head,middle-1,num);
else if (middle<num) return binarySearchRecursion(arr,middle+1,tail,num);
return -1;
}
public static int binarySearch(int[] arr,int num) {
int head = 0;
int tail = arr.length-1;
while (head<tail){
int middle = (head+tail)/2;
if(arr[middle]==num) return middle;
else if(middle>num) tail=middle-1;
else if(middle<num) head=middle+1;
}
return -1;
}
}
2.分治法
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
- 合并:将各个子问题的解合并为原问题的解。
汉诺塔问题
? 相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4JLlKjlA-1666596296728)(https://bkimg.cdn.bcebos.com/pic/d50735fae6cd7b896014d3e7052442a7d9330e5e?x-bce-process=image/resize,m_lfit,w_1280,limit_1/format,f_auto)]
package com.DataStructure;
public class HanNuoTower {
public static void main(String[] args) {
hanNuoTower(3,"A","B","C");
}
public static void hanNuoTower(int layer,String currentPt,String exchangePt, String targetPt){
// 如果只有塔层数仅有1 直接从当前位置移动到目标位置
if (layer==1) System.out.println(currentPt + "->" + targetPt);
else { // 塔层数大于1
// 将塔分为上下两部分 下部分有1层 上部分有layer-1层 转化为 移动两层的问题
// 将上面一层移动到空余位置
hanNuoTower(layer-1,currentPt,targetPt,exchangePt);
// 将下面一层移动到目标位置
System.out.println(currentPt + "->" + targetPt);
// 将空余位置的上层移动到目标位置
hanNuoTower(layer-1,exchangePt,currentPt,targetPt);
}
}
}
3.动态规划
动态规划(Dynamic programming)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。 动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。 关于动态规划最经典的问题当属背包问题。
经典的 01背包 与 无限背包问题
实例
找出最长递增子序列
int[] arr = {1,5,2,4,3}
递增序列有
/*
暴力遍历
- 从一开始
- 1 2 4
- 1 2 3
- 1 4
- 1 3
- 从五开始
- 5
- 从…
*/

观察上图 可以发现 1 2 4 这条路线
已经将 从4开始的路线一并计算 计算重复
暴力遍历会使得计算重复 时间复杂度 O(2n次方)
// 暴力解决
package com.DataStructure;
import static java.lang.Math.max;
public class DynamicPlan {
public static void main(String[] args) {
int[] arr = {1, 5, 2, 4, 3};
int maxNum = 0;
// 计算 从 数组元素 0-最后的每一个 最大子序列长度 选择最大的子序列长度
for (int i=0;i<arr.length;i++){
if (getMaxLength(arr,i)>maxNum) maxNum = getMaxLength(arr,i);
}
System.out.println(maxNum);
}
// 计算 arr 数组中 从 i 开始的 最大子序列的长度
public static int getMaxLength(int[] arr,int i){
// 到达数组中最后一个数
if (i==arr.length) return 1;
int maxLength = 1;
for (int j=i+1;j< arr.length;j++){
if (arr[j]>arr[i]){
maxLength = max(maxLength, getMaxLength(arr,j)+1);
}
}
return maxLength;
}
}
动态规划优化
package com.DataStructure.DynamicPlan;
import java.util.HashMap;
import java.util.Map;
import static java.lang.Math.max;
// 改进思路 将getMaxLength(0-最后一个元素)保存下来 无需计算
public class DynamicPlan {
public static Map<Integer,Integer> numMap = new HashMap();
public static void main(String[] args) {
int[] arr = {1, 5, 2, 4, 3};
int maxNum = 0;
// 计算 从 数组元素 0-最后的每一个 最大子序列长度 选择最大的子序列长度
for (int i=0;i<arr.length;i++){
if (getMaxLength(arr,i)>maxNum) maxNum = getMaxLength(arr,i);
}
System.out.println(maxNum);
}
// 计算 arr 数组中 从 i 开始的 最大子序列的长度
public static int getMaxLength(int[] arr,int i){
// 查找从i开始的最大子序列长度是否已经计算 已计算直接返回
if (numMap.containsKey(i)) return numMap.get(i);
// 到达数组中最后一个数
if (i==arr.length) return 1;
int maxLength = 1;
for (int j=i+1;j< arr.length;j++){
if (arr[j]>arr[i]){
maxLength = max(maxLength, getMaxLength(arr,j)+1);
}
}
// 保存从i开始的最大子序列长度
numMap.put(i,maxLength);
return maxLength;
}
}
动态规划非递归实现
package com.DataStructure.DynamicPlan;
import java.util.ArrayList;
import java.util.List;
import static java.lang.Math.max;
public class IteraciveDynamicPlan {
public static void main(String[] args) {
int[] arr = {1, 5, 2, 4, 3};
// 初始化列表为 [1,1,1,1,1] 代表该位置最长递增数列
List<Integer> L = new ArrayList<Integer>();
for (int num :
arr) {
L.add(1);
}
// 计算一个位置的 最长递增子数列 都会递归到最后 求出 L[arr.length-1] 直接倒序计算并保存即可
for (int i = arr.length - 1; i >= 0; i--) {
// 从i向后遍历
for (int j = i+1; j < arr.length; j++) {
// 如果arr[j] > arr[i] 说明构成递增 最长数加一
if (arr[j] > arr[i]) {
L.set(i, max(L.get(i), L.get(j) + 1));
}
}
}
System.out.println(L);
}
}
4.KMP
推荐视频:
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的[时间复杂度O(m+n) 。
package com.DataStructure;
import java.util.Arrays;
public class KMP {
public static void main(String[] args) {
String father = "ABAokasjf";
String son = "ABA";
System.out.println(calcBF(father,son));
System.out.println(Arrays.toString(getNextArr(son)));
System.out.println(calcKMP(father,son));
}
public static int calcBF(String father,String son){
char[] fatherChar = father.toCharArray();
char[] sonChar = son.toCharArray();
for (int i=0;i<fatherChar.length;i++){
int run=i;
int j=0;
while (fatherChar[run]==sonChar[j]){
if (j>=sonChar.length-1){
return i;
}
run++;
j++;
}
}
return -1;
}
public static int calcKMP(String father,String son){
// 得到next数组
int[] next = getNextArr(son);
// 给sonChar数组
son = " " + son;
char[] sonChar = son.toCharArray();
char[] fatherChar = father.toCharArray();
for (int i=0,j=1;i<fatherChar.length;){
// 匹配第一个字符是否相等 相等 j++
if (fatherChar[i]==sonChar[j]){
j++;
i++;
// 判断是否到达末尾 到达末尾返回 i
if (j>=sonChar.length-1){
return i+1-(sonChar.length-1);
}
// 继续循环
continue;
}
// 不匹配
else{
// 为0将i移至下一位
if (next[j-1]==0){
i++;
}
// 将当前j的值移至next数组中的值
else {
j=next[j-1];
}
}
}
return -1;
}
// 获取next数组
public static int[] getNextArr(String son){
char[] sonChar = son.toCharArray();
int[] nextNum = new int[sonChar.length];
for(int i=0;i<sonChar.length;i++){
int nextNUM = 0;
int head=0,tail=1;
int run = tail;// 指针回溯定义
while (tail<i){
if (sonChar[head]==sonChar[tail]){
nextNUM++;
tail++;
head++;
}
else {
head=0;
run++;
tail=run; // 指针回溯使用
nextNUM = 0;
}
}
// next数组值为 最大前后缀长度加1
nextNum[i] = nextNUM+1;
}
nextNum[0]=0;
return nextNum;
}
}
5.贪心算法
与动态规划对比
动态规划是下一个子问题的解与已经得到的子问题解有关。而贪心算法仅仅关注单次结果
- 共同点:取最优子结构的解,一步一步解决问题
- 不同点:贪心的取局部最优做全局最优,动态规划递推全局最优
- 深层区别:贪心是动态规划在最优子结构评价纬度单一时的一种特殊解法
注意:之后讲的 普利姆算法与克鲁斯卡尔算法也是贪心算法
// 评价最优条件是什么?
// 循环->未解决问题 && 还有解
// 从可能的解中取出最优解
// 执行最优解
// 缩小问题规模->双指针,for循环,减去最优解.
- 贪婪算法(贪心算法)是指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法
- 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果
实例
假设存在如下表的需要付费的广播台,以及广播台信号可以覆盖的地区。如何选择最少的广播台,让所有的地区都可以接收到信号
| 广播台工 | 覆盖地区 |
|---|---|
| K1 | “北京”,“上海”, “天津” |
| K2 | “广州” , “北京”,“深圳” |
| K3 | “成都” ,“上海”,“杭州” |
| K4 | “上海”,“天津” |
| K5 | “杭州”,“大连” |
使用贪婪算法,效率高:
目前并没有算法可以快速计算得到准备的值,使用贪婪算法,则可以得到非常接近的解,并且效率高。选择策略上,因为需要覆盖全部地区的最小集合:
- 遍历所有的广播电台,找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区,但没有关系)
- 将这个电台加入到一个集合中(比如ArrayList),想办法把该电台覆盖的地区在下次比较时去掉。
- 重复第1步直到覆盖了全部的地区
package com.DataStructure;
import java.util.ArrayList;
// java的语法一言难尽 与 python list相比
public class greedAlgorithm {
public static void main(String[] args) {
// 初始化城市列表
ArrayList<ArrayList> radioNumber = new ArrayList<ArrayList>();
ArrayList<String> k1 = new ArrayList<>();
k1.add("A");
k1.add("B");
k1.add("C");
radioNumber.add(k1);
ArrayList<String> k2 = new ArrayList<>();
k2.add("D");
k2.add("A");
k2.add("E");
radioNumber.add(k2);
ArrayList<String> k3 = new ArrayList<>();
k3.add("F");
k3.add("B");
k3.add("G");
radioNumber.add(k3);
ArrayList<String> k4 = new ArrayList<>();
k4.add("B");
k4.add("C");
radioNumber.add(k4);
ArrayList<String> k5 = new ArrayList<>();
k5.add("G");
k5.add("H");
radioNumber.add(k5);
System.out.println(radioNumber);
System.out.println(findRadioNumber(radioNumber));
}
public static ArrayList findRadioNumber(ArrayList radioList){
// 创建结果列表
ArrayList<Integer> resultList = new ArrayList<Integer>();
System.out.println("Began");
boolean flag = true;
while (flag){
//1. 找到包含电台最多的城市
int maxLength=0,maxIndex=0;
for (int i=0;i<radioList.size();i++){
if (((ArrayList)radioList.get(i)).size() > maxLength){
maxIndex=i;
maxLength=((ArrayList)radioList.get(i)).size();
}
}
//2. 将其添加进入结果
ArrayList<String> choiceRadio = (ArrayList)radioList.get(maxIndex);
resultList.add(maxIndex);
//3. 将其暂时设置为空数组
radioList.set(maxIndex,new ArrayList<String>());
//4. 删除radioList中其中已选择的城市的元素的元素
for (Object list :
radioList) {
list = (ArrayList<String>) list;
for (String str :
choiceRadio) {
((ArrayList<?>) list).remove(str);
}
}
//5. 判断是否挑选完毕 没有未覆盖区域
flag=false;
for (Object list :
radioList) {
list=(ArrayList)list;
if (((ArrayList<?>) list).size()!=0){
flag=true;
}
}
}
return resultList;
}
}
6.Prim
推荐视频:
最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示_哔哩哔哩_bilibili
最小生成树算法 普利姆算法
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
// 图的结构
package com.DataStructure;
import javafx.scene.shape.Arc;
import java.util.ArrayList;
// 自己写的图可能不太规范
// 使用邻接表法实现
public class Graph {
// 头节点列表
public ArrayList<HeadNode> nodeList = new ArrayList<>();
// 添加头节点
public void addHeadNode(int data){
HeadNode node = new HeadNode(data);
this.nodeList.add(node);
}
// 添加边 为头节点 连接其他节点
// i 为头节点 j 为要连接哪个节点 weightval 边的权值大小
public void linkNode(int i,int j,int weightVal){
GraphNode run = this.nodeList.get(i).nextNode;
if (run==null) this.nodeList.get(i).nextNode = new GraphNode(weightVal,j);
else{
while (run.nextNode!=null){
run = run.nextNode;
}
run.nextNode = new GraphNode(weightVal,j);
}
}
}
class GraphNode{
public int value; // 边的权值
int node; // 指向的节点
public GraphNode nextNode = null; // 预留下一个节点的空间
public GraphNode(int value,int node){
this.value=value;
this.node=node;
}
@Override
public String toString() {
return "GraphNode{" +
"value=" + value +
", node=" + node +
", nextNode=\n" + nextNode +
'}';
}
}
class HeadNode{
public int data; // 节点的值
public GraphNode nextNode = null; // 指向的节点
public HeadNode(int data){
this.data=data;
}
@Override
public String toString() {
return "HeadNode{" +
"data=" + data +
", nextNode=\n" + nextNode +
'}';
}
}
package com.TenAlgorithms;
// 自己写的图结构
import com.DataStructure.Graph;
import java.util.Arrays;
/**
* @author: LonelySnowman
* @Pcakage: com.TenAlgorithms.Prim
* @Date: 2022年09月30日 16:54
* @Description:
*/
public class Prim {
public static final int inf = 99;
public static void main(String[] args) {
Graph myGraph = Graph.getDefaultGraph();
boolean[] selected = new boolean[6]; // 该节点是否被选择 默认为false
int[] minDist = new int[6]; // 最小权值
int[] parent = new int[6]; // 父节点
// 初始化上面三个数组
selected[0] = true; // 第一个节点默认已被选择
for (int i=0;i<minDist.length;i++){
minDist[i] = inf;
}
for (int i=0;i<parent.length;i++){
parent[i] = -1; // -1 为无父节点
}
System.out.println(Arrays.toString(selected));
System.out.println(Arrays.toString(minDist));
System.out.println(Arrays.toString(parent));
Prim(selected,minDist,parent,myGraph);
}
static void Prim(boolean[] selected,int[] minDist,int[] parent,Graph myGraph){
// 不断循环 Update Scan Add 即可 直到全部节点都被加入最小生成树
boolean flag = true;
int search = 0; // 从0开始查找
while (flag){
// Update 遍历该节点的边 更新 最小权值minDist 与 父节点 parent
Graph.GraphNode run = ((Graph.HeadNode)myGraph.nodeList.get(search)).nextNode;
while (run!=null){ // 遍历更新
// 选择没有加入最小生成树的节点 且需要连接值小于保存值
if (run.value<minDist[run.node] && !selected[run.node]){
// 更新两个数组
minDist[run.node]=run.value;
parent[run.node]=search;
}
run = run.nextNode;
}
// Scan 扫描得到权值最小的节点
int minIndex=0;
int min=inf;
for (int i=0;i<minDist.length;i++){
// 已被选择的节点无需计算
if (minDist[i]<=min&&!selected[i]) {
min = minDist[i];
minIndex = i;
}
}
// Add 将此节点加入最小生成树
selected[minIndex]=true;
// 下一个搜寻刚刚加入的节点
search=minIndex;
// 判断是否全部加入
flag = false;
for (int i=0;i<selected.length;i++){
if (!selected[i]) flag = true;
}
}
System.out.println("最小生成树为:");
System.out.println(Arrays.toString(selected));
System.out.println(Arrays.toString(minDist));
System.out.println(Arrays.toString(parent));
}
}
7.Kruskal
推荐视频:
最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示_哔哩哔哩_bilibili
最小生成树算法 克鲁斯卡尔算法
思路:
/*
将所有的边全部 ‘放入’ 数组中
将数组根据权值大小从小到达进行排序
将权值最小的边放入图中
if 生成环{
选下一位权值最小的边
}
if 没有生成环{
重复上述操作
}
*/
8.Dijkstra
最短路径查找算法
Dikstra适用于从一个点到其他点的最短路径,需要一个图中任意两点的最短路径需要对每一个点进行Dikstra算法,下面有效率更高的Floyd算法
视频演示:【算法】最短路径查找—Dijkstra算法_哔哩哔哩_bilibili
代码演示:Dijkstra算法详解 通俗易懂 - 知乎 (zhihu.com)
Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法,时间复杂度 O(n2)
这里使用 -1 表无穷大,下面是 Java 代码和测试案例
// 此方法只求出了最短距离的值
// 没有求出到达最短距离的路径
// 计算路径需要额外数组保存 到达该点的前一位节点 最后逆序输出即可
public class Dijkstra {
public static int[] dijkstra(int[][] graph,int startVertex){
//初始化 以求出最短路径的点 result[]
int length = graph.length;
int[] result = new int[length];
for (int i = 0; i < length; i++) {
result[i] = -1;
}
result[startVertex] = 0 ;
// 初始化 未求出最短路径的点 notFound[]
int[] notFound = new int[length];
for (int i = 0; i < length; i++) {
notFound[i] = graph[startVertex][i];
}
notFound[startVertex] = -1;
// 开始 Dijkstra 算法
for (int i = 1; i < length; i++) {
//1. 从「未求出最短路径的点」notFound 中取出 最短路径的点
//1.1 找到最短距离的点
int min = Integer.MAX_VALUE;
int minIndex = 0;
for (int j = 0; j < length; j++) {
if (notFound[j] > 0 && notFound[j] < min){
min = notFound[j];
minIndex = j;
}
}
//1.2 将最短距离的点 取出 放入结果中
result[minIndex] = min;
notFound[minIndex] = -1;
//2. 刷新 「未求出最短距离的点」 notFound[] 中的距离
//2.1 遍历刚刚找到最短距离的点 (B) 的出度 (BA、BB、BC、BD)
for (int j = 0; j < length; j++) {
// 出度可通行(例如 BD:graph[1][3] > 0)
// 出度点不能已经在结果集 result中(例如 D: result[3] == -1)
if (graph[minIndex][j] > 0
&& result[j] == -1){
int newDistance = result[minIndex] + graph[minIndex][j];
//通过 B 为桥梁,刷新距离
//(比如`AD = 6 < AB + BD = 4` 就刷新距离)( -1 代表无限大)
if (newDistance < notFound[j] || notFound[j]==-1){
notFound[j] = newDistance;
}
}
}
}
return result;
}
/** 测试案例 */
public static void main(String[] args) {
char[] vertices = new char[]{'A','B','C','D'};
int[][] graph = new int[][]{
{0, 2, -1, 6}
, {2, 0, 3, 2}
, {-1, 3, 0, 2}
, {6, 2, 2, 0}};
int[] dijkstra = dijkstra(graph, 0);
for (int i : dijkstra) {
System.out.println(i);
}
}
}
/*
输出结构
0
2
5
4
*/
9.Floyd
推荐视频:
图论最短距离(Shortest Path)算法动画演示-Dijkstra(迪杰斯特拉)和Floyd(弗洛伊德)_哔哩哔哩_bilibili
支持Floyd算法的推论
一下 x -> y 表示 x节点到y节点的距离
-
节点x 到 节点y 的最短路径会经过节点m则:
? x->y = x->m + m->y
-
节点x 到 节点y 的最短路径不会经过节点m则:
? x->y < x->m + m->y
// 优雅 实在是太优雅了! 这个算法很离谱
// I Love It
// 以下为核心算法 一个三层for循环
// 意义为循环 不同的 i->k->j 的距离 不停的寻找中间点
for(k=0;k<n;k++) //中转站0~k
for(i=0;i<n;i++) //i为起点
for(j=0;j<n;j++) //j为终点
// 此处 -> 表示当前距离 非最短距离
// 如果 i->k + k->j < i->j
// 则说明 最短距离需要经过k
if(D[i][k]+D[k][j]<D[i][j]){
// 更新最短距离
D[i][j]=D[i][k]+D[k][j];
// 更改中间经过的点 经过i->k
S[i][j]=S[i][k]
}
// D矩阵 与 S矩阵的解释
// D矩阵 D[i][k] 为 节点i 到节点k 的最小距离
// S矩阵
// S[i][k] == k 说明 i->k 中间没有任何节点 直接到k
// S[i][k] != k 说明 i->k 中间存在其他节点假设值为 m 需要继续查看 S[i][m]
10.马踏棋盘算法(骑士周游)
推荐视频:
2021年春浙江工业大学算法课程习题-骑士巡游问题问题_哔哩哔哩_bilibili
使用方法:递归 回溯 剪枝策略
视频讲解为python实现 下面由JAVA演示
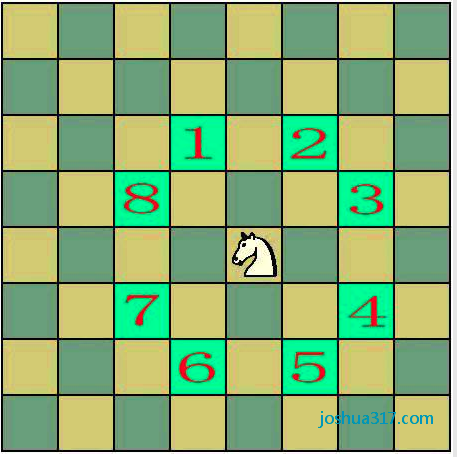
跳马问题也称为骑士周游问题,是算法设计中的经典问题。其一般的问题描述是:
考虑国际象棋棋盘上某个位置的一只马,它是否可能只走63步,正好走过除起点外的其他63个位置各一次?如果有一种这样的走法,则称所走的这条路线为一条马的周游路线。试设计一个算法找出这样一条马的周游路线。
此题实际上是一个汉密尔顿通路问题,可以描述为:
在一个8×8的方格棋盘中,按照国际象棋中马的行走规则从棋盘上的某一方格出发,开始在棋盘上周游,如果能不重复地走遍棋盘上的每一个方格,
这样的一条周游路线在数学上被称为国际象棋盘上马的哈密尔顿链。请你设计一个程序,从键盘输入一个起始方格的坐标,由计算机自动寻找并打印
出国际象棋盘上马的哈密尔顿链。
// java版实现
public class KnightTour {
// 定义棋盘大小 n*n
static int n = 5;
// 定义棋盘
static int[][] chessboard = new int[n][n];
// 定义骑士的移动方式 只有八种 马走“日”字
static int[] runX = {-2,-2,-1, 1, 2, 2, 1,-1};
static int[] runY = {-1, 1, 2, 2,-1, 1,-2,-2};
public static void main(String[] args) {
knightRun(0,0,1);
}
// 编写检查算法 检查骑士是否跳出棋盘
static boolean checkKnight(int x, int y){
// 如果骑士没有跳出棋盘且该位置骑士没有到达过 则可以跳跃
if ((x>=0&&x<n) && (y>=0&&y<n) && chessboard[x][y]==0) return true;
else return false;
}
// 编写回溯算法 骑士遍历所有可以跳往的位置
// x 与 y 为当前骑士到达的位置坐标
// num为骑士第几次跳跃
static boolean knightRun(int x,int y,int num){
// 是否跳跃完毕
boolean flag = false;
// 设置该位置的值为num
// 跳到该位置
chessboard[x][y] = num;
// 已经遍历完全部位置 跳跃完毕 设定递归结束条件
if (num == n*n){
printChessBoard();
flag = true;
return flag;
}
// 骑士向下一步跳跃
// 骑士有八种走法依次遍历
for (int i=0;i<8;i++){
// 如果可以向该位置跳跃
if (checkKnight(x+runX[i],y+runY[i])){
// 跳吧
// 保留flag判断是否完成跳跃
flag = knightRun(x+runX[i],y+runY[i], num+1);
// 剪枝策略 避免不必要的遍历
if(flag) break;
// 如果flag=false 说明骑士无路可走 该跳跃路线失效 跳跃失败
// 进行 ”回溯“ 将之前跳跃过的路都清空
// 该位置没有跳过 换一条路试试
else chessboard[x+runX[i]][y+runY[i]] = 0;
}
}
return flag;
}
// 输出棋盘 | 二维数组
static void printChessBoard(){
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
System.out.print(chessboard[i][j] + " ");
}
System.out.println();
}
}
}
骑士周游算法可进行优化
我们发现我们是将可行的落脚点分别进行一次递归
如果我们将他落脚点处的下一次的可行落脚点的数量进行统计
排序后选择下一次落脚点最少的位置进行跳跃(减少For中递归的次数 减少栈的开销)
会发现改进后骑士会有限选择边缘进行下一步落脚点 先四周 再中心