以下题目均需要掌握递归遍历
一、LeetCode104.二叉树的最大深度
? ? ? ? 1:题目描述(104.二叉树的最大深度)
????????给定一个二叉树,找出其最大深度。
????????二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
????????说明:?叶子节点是指没有子节点的节点。
????????示例:
????????????????给定二叉树 [3,9,20,null,null,15,7],

????????返回它的最大深度?3 。?
? ? ? ? 2:解题思路:
? ? ? ? 解法一:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
# 求二叉树的最大高度就是求二叉树的最大深度
# 最大高度使用后序遍历:左右中
# 最大深度使用前序遍历:中左右
def Depth(cur): #
if cur == None:
return 0 # 当节点为空,返回0
lefthight = Depth(cur.left) # 求左节点的高度
righthight = Depth(cur.right) # 求右节点的高度
hight = 1 + max(lefthight, righthight) # 去左右节点高度的最大值,然后+1就是节点的高度
return hight
if not root:
return 0
res = Depth(root)
return res? ? ? ? 解法二:迭代法,使用队列来实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
queue = []
s = 0
if not root:
return s # 根节点为空,直接返回0
queue.append(root) # 根节点不为空,将根节点加入到队列queue中
while queue: # 队列queue不为空
q_len = len(queue) # 统计每层的节点数
s += 1 # 层数自加1
while q_len: # 每层剩余的节点数不为0
node = queue.pop(0) # 弹出节点
q_len -= 1 # 弹出节点后,剩余的节点数减1
if node.left: # 弹出节点的左节点不为空,则加入队列
queue.append(node.left)
if node.right: # 弹出节点的右节点不为空,则加入队列
queue.append(node.right)
return s # 当队列为空时,s就是二叉树的最大深度二、LeetCode559.n叉树的最大深度
? ? ? ? 1:题目描述(559.n叉树的最大深度)
????????给定一个 N 叉树,找到其最大深度。
????????最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
????????N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
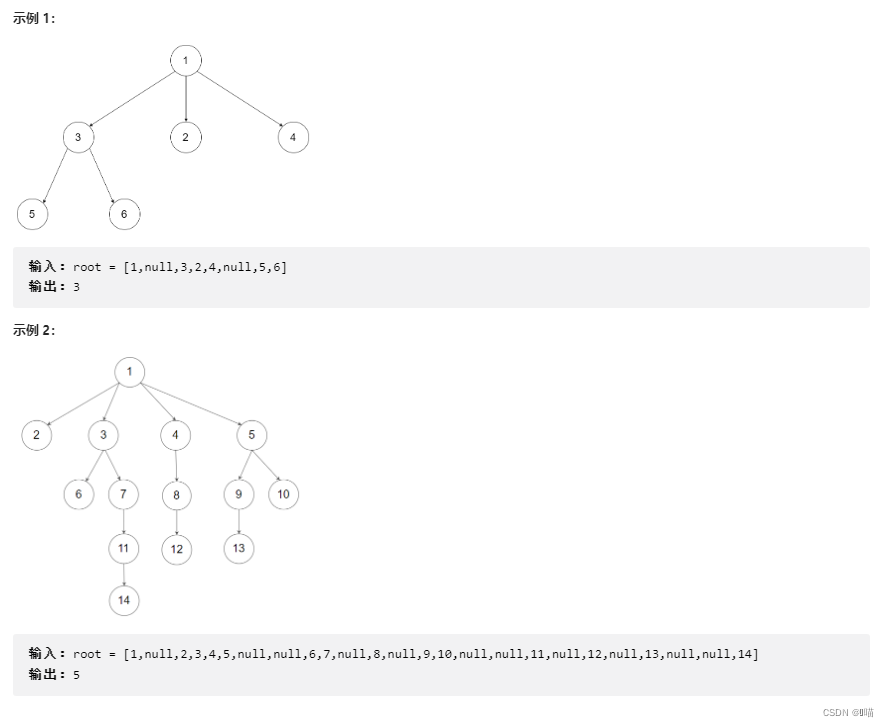
? ? ? ? 2:解题思路
? ? ? ? 解法一:递归法
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
# 递归法
if not root:
return 0 # root为空,直接返回0
depth = 0 # 统计当前最大深度
for i in range(len(root.children)): # 遍历每个节点的所有孩子节点
# self.maxDepth(root.children[i]),继续遍历当前节点的孩子节点
depth = max(depth, self.maxDepth(root.children[i])) # 取当前的深度与节点的孩子节点深度中的最大值
return depth + 1 # 最后加上根节点? ? ? ? 解法二:迭代法?
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
# 迭代法
res = 0
if not root:
return res
from collections import deque
queue = deque([root])
while queue:
q_len = len(queue)
res += 1
for i in range(len(queue)):
node = queue.popleft()
if node.children:
queue.extend(node.children)
return res 三、LeetCode111.二叉树的最小深度
? ? ? ? 1:题目描述(111.二叉树的最小深度)
????????给定一个二叉树,找出其最小深度。
????????最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
????????说明:叶子节点是指没有子节点的节点。
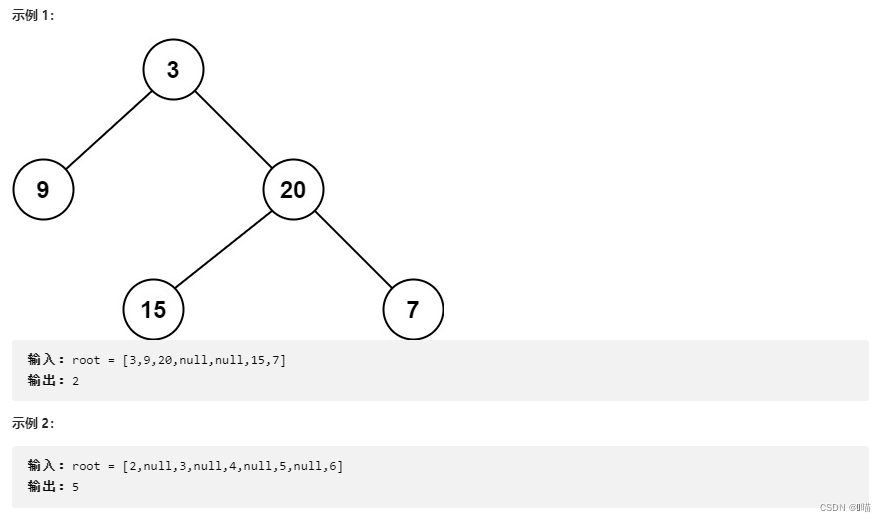
? ? ? ? 2:解题思路
? ? ? ? 解法一:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
# 递归法
def Depth(cur):
if cur == None:
return 0 # 节点为空了,返回高度0
leftdepth = Depth(cur.left) # 获取左子树的高度
rightdepth = Depth(cur.right) # 获取右子树的高度
if cur.left == None and cur.right != None:
return 1+rightdepth # 当左子树为空,右子树不为空时,此时高度应该取右子树的高度,再加1
if cur.left != None and cur.right == None:
return 1+leftdepth # 当左子树不为空,右子树为空时,此时高度应该取左子树的高度,再加1
# 当左右子树都不为空时,就去左右子树高度的最小值,再加1
depth = 1 + min(leftdepth,rightdepth)
return depth
if not root:
return 0
res = Depth(root)
return res? ? ? ? ?解法二:层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
# 层序法
queue = []
s = 0
if not root:
return s
queue.append(root)
while queue:
q_len = len(queue) # 统计每层的节点数
s += 1 # 统计深度
while q_len:
node = queue.pop(0) # 每层剩余节点不为0时,弹出元素
q_len -= 1 # 弹出元素后,剩余节点数减1
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# 当节点的左右子节点均为空时,就是最小深度
if node.left == None and node.right == None:
return s四、LeetCode222.完全二叉树的节点个数
? ? ? ? 1:题目描述(222.完全二叉树的节点个数)
????????给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
????????完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~?2h?个节点。
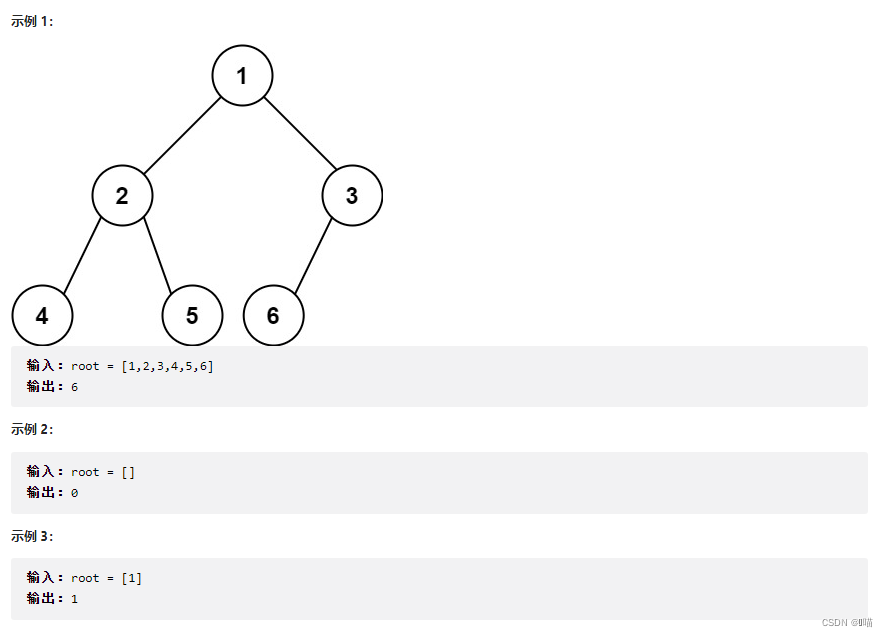
? ? ? ? 2:解题思路
? ? ? ? 解法一:使用完全二叉树的特点,进行递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
# 利用完全二叉树的特性
# 当最底层节点填满后,就是一个满二叉树,可以使用 2*2-1的方式直接求节点的数量
# 以示例一为例,左子树是一个满二叉树,右子树不是一个满二叉树
# 因此可以判断左子树是不是满二叉树,是则用公式求出节点数量
# 使用递归
def getNum(cur):
if cur == None:
return 0
# 定义两个左右两个指针,去遍历节点的左侧和右侧节点
left = cur.left
right = cur.right
left_count = 0 # 统计左侧节点的个数
right_count = 0 # 统计右侧节点的个数
while left:
left = left.left
left_count += 1 # 每往下遍历一个节点,左侧节点个数加1
while right:
right = right.right
right_count += 1 # 每往下遍历一个节点,右侧节点个数加1
# 如果left_count == right_count,则说明是一个满二叉树
if left_count == right_count:
return (2**(left_count+1)) - 1 # left_count = 0时,应该是2**1-1,所以使用**,需要left_count+1
# return (2<<left_count) - 1 # left_count = 0时,2<<left_count相当于2**1
# 如果left_count != right_count,则说明不是一个满二叉树,再分别遍历左右子树
leftNum = getNum(cur.left) # 求左子树的节点数
rightNum = getNum(cur.right) # 求右子树的节点数
return leftNum + rightNum + 1 # 左子树节点数+右子树节点数+1,就是二叉树的节点数
if not root:
return 0
res = getNum(root)
return res? ? ? ? 解法二:使用普通二叉树的层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
# # 层序遍历
queue = []
s = 0
if not root:
return s
queue.append(root)
while queue:
q_len = len(queue)
while q_len:
node = queue.pop(0)
q_len -= 1
s += 1
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return s? ? ? ? 解法三:使用普通二叉树的递归遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
# # 当做普通二叉树,使用递归-后序遍历
def count_node(cur):
if cur == None:
return 0 # 节点为空,0个节点
left_count = count_node(cur.left) # 统计左子树的节点
right_count = count_node(cur.right) # 统计右子树的节点
return 1+left_count + right_count # 左子树的节点+右子树的节点+1为二叉树的节点
if not root:
return 0
res = count_node(root)
return res