大家好!这篇主要说一下链表里的带环问题。

141. 环形链表
难度 简单 题目链接
我们先来看一下题目给的例子:
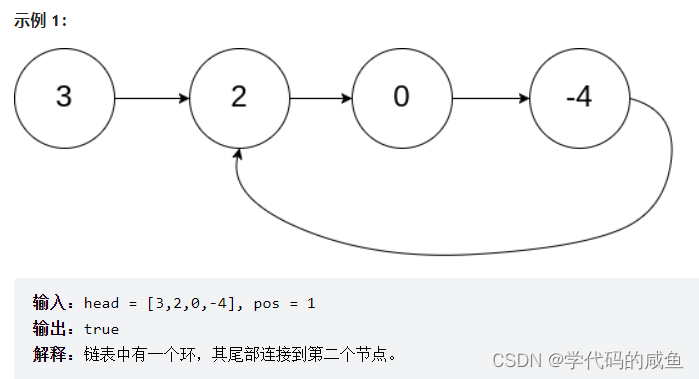
那么这道题,我们该如何来求解呢?
解决思路:
根据带环链表的形状,我们可以抽象一下:

我们用快满指针来做,一个fast走两步,一个slow走一步。

然后我们假设当fast走到环的入口时,slow走到一半:

当slow进环以后,fast开始进行追赶模式,fast追赶slow:

如果带环,fast总会有个时间追上slow。

代码如下:
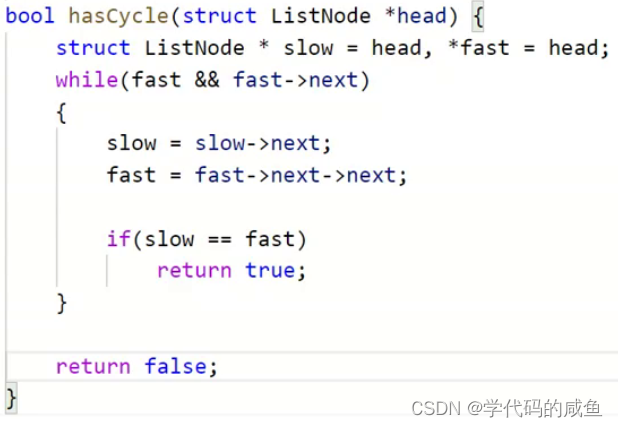
这道题本身难度不大,关键是我们如何证明呢?
为什么快指针每次走两步,慢指针走一步可以?

slow进环开始追击,假设slow进环以后,slow和fast之间的距离是N

每次追击,距离减1。又因为N它是一个整数,所以总有一次会变为0,会追上。
第二个问题:快指针一次走3步,走4步,…n步行吗?
我们先分析一下slow走一步,fast走三步:

slow进环以后,fast开始追击slow。假设它们之间的追击距离为N,环的长度为C

每次追击,fast和slow之间的距离缩小2。那么根据上面,我们可以进行分析:

那么N是偶数,它能追上。那么N是奇数呢,它变成-1,-1的意思就是slow和fast之间的追击距离为C-1了。
那么我们还按照之前的分析,如果C-1是偶数,那么可以追上。如果C-1是奇数,那么就永远追不上了。
那么剩下的步数,也是按照这样去分析。
142. 环形链表 II

难度 中等 题目链接
示例:
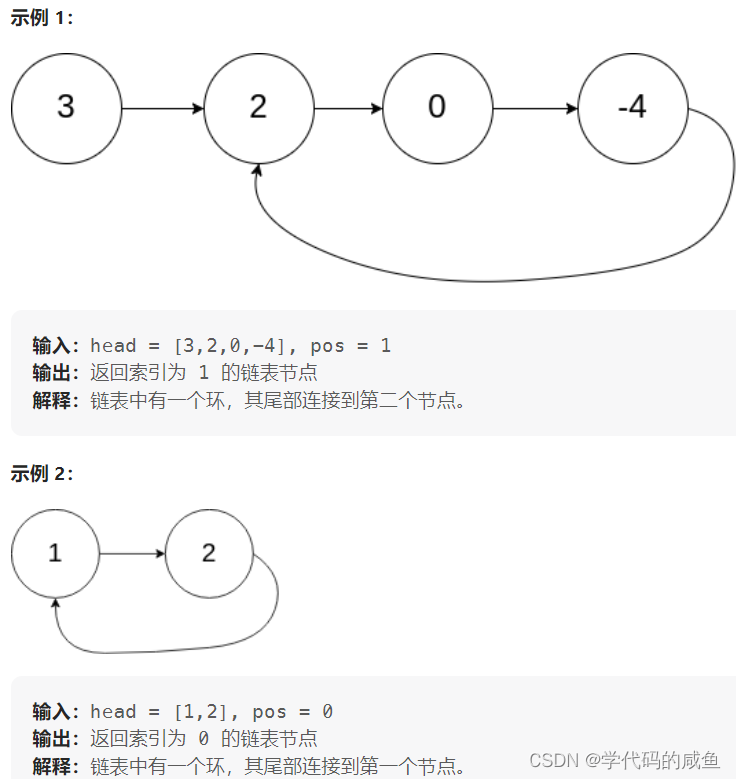
方法1:公式做法

我们假设slow和fast在此处相遇。

那么一个指针在相遇点走,一个指针在开头走。那么它们一定在环的入口相遇。
那么我们如何证明这个公式呢?

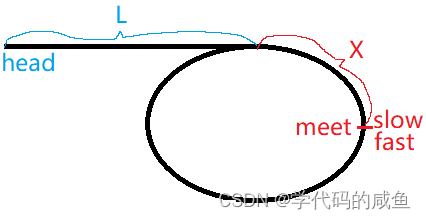
我们假设前面的长度为L,后面从环的入口到相遇点为X。
那么slow走的距离为:L+X
那么现在有一个问题:slow有没有可能在环里走一圈了,才被fast追上呢?
答案是:没这个可能。
因为,fast一次走两步,slow一次走一步。那么fast走的距离是slow走的距离的2倍。所以,如果slow走一圈,fast都走两圈了。
那么fast走的距离呢?

这是我们进行的假设。可能有的同学会说fast走的距离是:L+X+C。但是不是这样的,我们来看下面这个例子:

从这个例子可以看出:fast走到环的入口时,slow走到L的一半。此时,slow每走一步,fast就会绕环一圈。所以fast走的距离:不一定是L+X+C,而是L+N*C+X。
然后,根据fast走的距离是slow距离的2倍。所以,2*(L+X)=L+N * C+X,L+X=N * C,L=N*C-X。所以,我们根据这个公式就能得出:一个指针从meet走,一个指针从head走,它们能在环的入口处相遇。
那么我们把代码写一下:
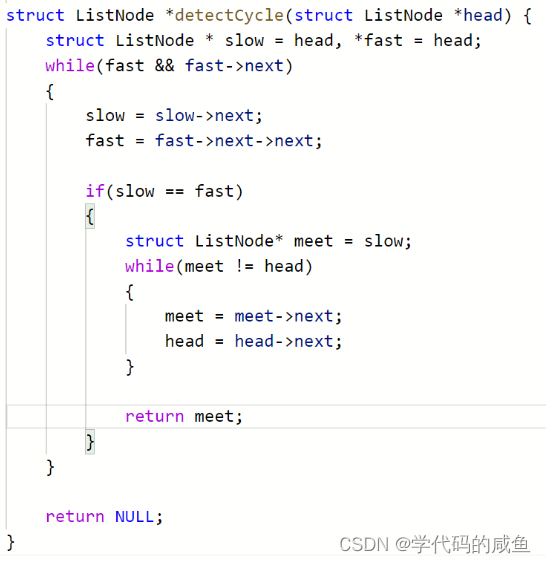
方法2:断开做法
思路就是:转换成链表相交问题

这里是相遇的位置,然后我们在相遇的这里把它断开:

然后我们就可以当作两个链表相交的问题了。
如何断开呢?
struct ListNode* headA=head;
struct ListNode* headB=meet->next;
meet->next=NULL;
实现代码如下:
