?????
???
????????快算排序 Quick Sort ,可能是应用最为广泛的算法,被视为20世纪科学和工程领域的十大算法之一。其流行的原因是因为它实现简单,可适用于不同数据,并且在一般场景下比其他算法要更快。其优点是:
可借用一个很小空间的辅助栈来进行原地排序;
对于长度为N的数组,其时间复杂度为 NlogN;
快速排序的内循环短小,这意味它无论在理论上还是在实际中,它都要更快。
缺点:
????????要小心的避免错误,防止性能退化为N2 。
算法思想:
? ? ? ? 快速排序 和 归并排序一样都是使用了分治思想的排序算法。他们都是将一个数组,一分为二,独自独立排序。 归并排序是将数组分为两个子数组分别排序,并将有序的子数组归并将整个数组进行排序;而快速排序是当子数组都有序了之后,整个数组自然就实现了有序。归并的切分位置就在数组中间位置;而快速排序的切分位置partition 取决于数组的内容。
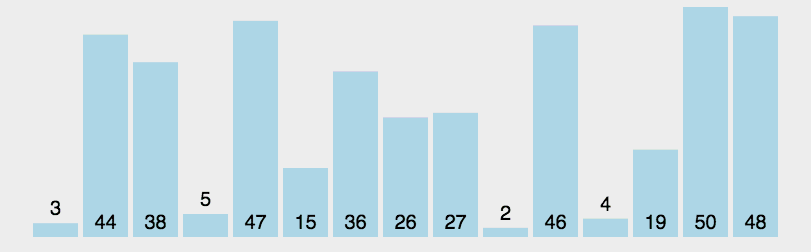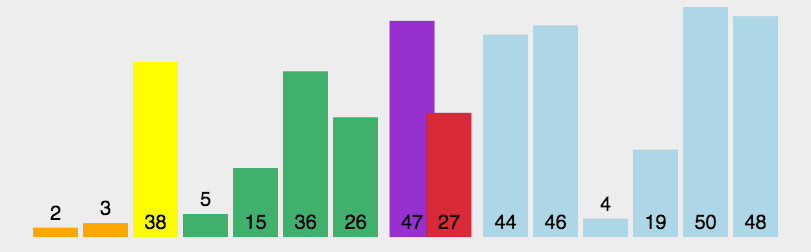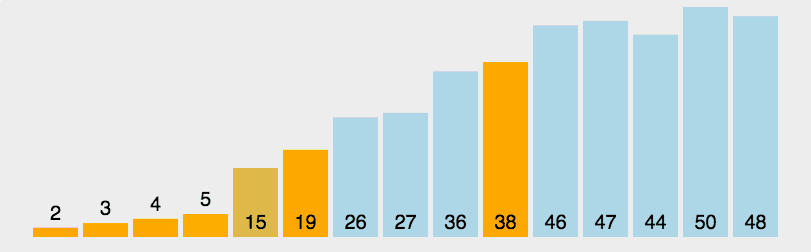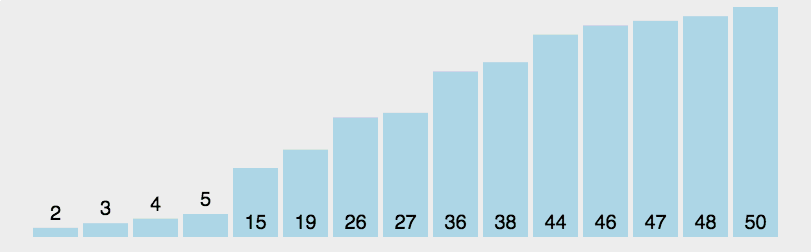
Partition过程大致如图所示:

?
? ? ? ?快速排序需要推举出一个元素来作为我们的基准元素;如图所示:我们推举出我们的首个元素作为基准元素(V)。帮助我们的基准元素找他应该所处的位置过程,我们将其命名为 Partition的过程,即找到 j 的过程。
? ? ? ? 结合如图所示,我们来看我们应该如何去做这件事:
在这个过程中,我们需要满足的V前面的元素是不大于V的,V后面的元素是不小于V的。即 arr[l+1...j] < v && arr[j+1...i-1] > v
? ? ? ? ?图中变量 , v :基准元素? ,l :元素开始位置索引,j基准位置索引,i 遍历比较过程中的当前时刻的位置索引;
蓝色元素e本身比较前的位置就处于不小于V的位置,如果发现e 大于 V 不动,i++遍历下一个元素;如果发现当前遍历元素e小于V,则需要将e和紫色部分的首元素交换,并且j++。如此进行下去,直到i遍历完整个数组后,把l位置所在元素,和 j 位置所在元素 进行交换后,即可完成整个Partition的过程。
算法实现:
基于以上内容,我们来实现第一版的算法基本实现:
package com.cosyit.offer.algorithms;
import java.util.Arrays;
public class QuickSort1 {
private static void quickSort(Comparable[] a, int n) {
__quickSort(a, 0, n - 1); // a[0] - a[length-1]
}
private static void __quickSort(Comparable[] a, int l, int r) {
//设置临界条件。 obscure
if (l >= r) return;
//隔板分区
int p = partition(a, l, r);
// l 到 p-1 的分区部分 进行快速排序。
__quickSort(a, l, p - 1);
// p+1 到 r 的分区部分 进行快速排序。
__quickSort(a, p + 1, r);
}
/**
* 推举出一个元素作为隔板元素以进行分区,隔板分区后该元素将处于其顺序的位置,并返回该隔板元素的索引。
* 元素a[p]的隔板效果:左边的比隔板元素小 a[l...p-1] < arr[p],右边都比隔板元素大 a[p] < a[p+1...r]
*
* @param a 传入的数组。
* @param l 左边界元素索引。
* @param r 有边界元素索引。
* @return 隔板操作后的,隔板位置索引。
*/
private static int partition(Comparable[] a, int l, int r) {
// 1.推举出一个元素,这里我们推举我们的头部元素为隔板元素。
Comparable v = a[l];
// 2.遍历整个数组。a[l+1...j]<v ,v < a[j+1...i),i是开区间,因为i的元素是我们当前需要考察的元素。
int j = l; //j:不大于v左边分区的尾部元素位置索引。
/**
* 这里有一个定义的技巧,就是 j 和 i 的初始值设计:
* * 为什么 把j的初始化值设置为l , 因为这样设计 a[l+1...j]即a[l+1...l],保证了小于v的分区,从开始是不存在的分区。
* * 为什么 把i的初始化值设置为l+1, 因为这样设计 a[j+1...i]即a[l+1...l+1) ,保证了大于v这个分区,从开始是不存在的分区。
*/
for (int i = l + 1; i <= r; i++) {
if (less(a[i], v)) {
swap(a, j + 1, i);
j++;
}
}
//放置隔板:i 遍历完的时候,元素v即a[l] 和 j进行交换。把j的标记位置索引 j 返回。
swap(a, l, j);
return j;
}
private static void swap(Comparable[] arr, int i, int j) {
Comparable temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
private static boolean less(Comparable a, Comparable b) {
return a.compareTo(b) < 0;
}
public static void main(String[] args) {
Integer[] arr = {6, 7, 1, 4, 3, 5, 2, 0};
quickSort(arr, arr.length);
System.out.println(Arrays.toString(arr));
}
}
基础算法的改进:
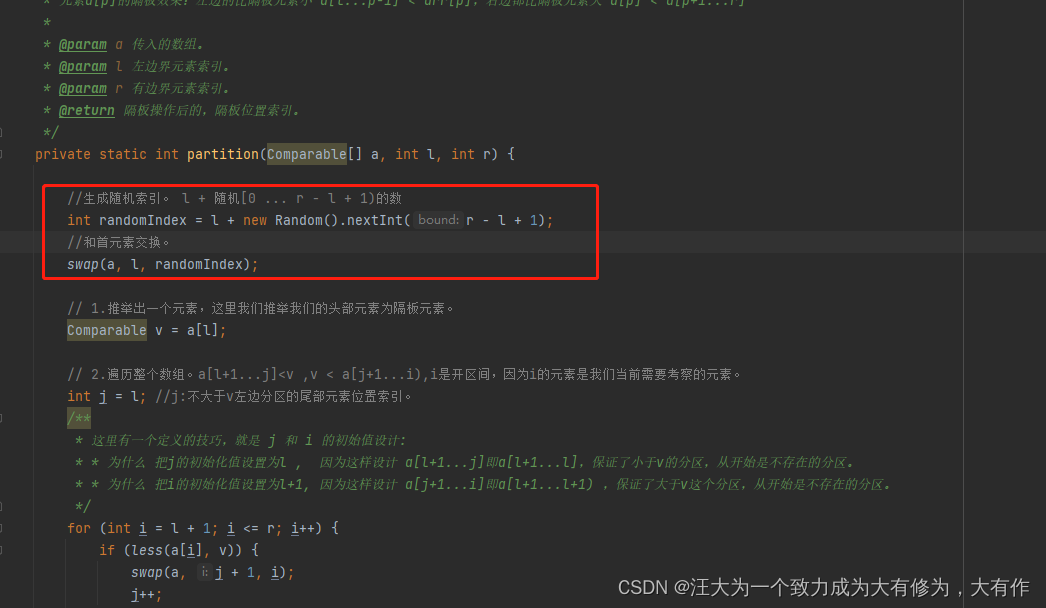
? ? ? 改进1:? 推举首元素为隔板元素的是有弊端的,因为往往人们处理的数据大概率会是一个近乎有序的数组,这样的数据在进行 递归时候,分区的递归树的高度会很高,递归树的平衡度会很差。基于这个问题,我们应使 隔板元素 保持随机性,来避免这个问题。固添加如下代码以做优化:
?
改进2:如果处理切分元素有大量重复元素,而导致切分不平衡的情况,栈深度会变大。
 ???????
???????
?
优化一下思路,如图所示:

??????????之前,我们把大于V和小于V的放在了数组的一端,现在把大于V和小于V的放在数据的两端。
????????如图所示:i,j 的位置为比较元素e,i++往右跑,j--往左跑。
i在遍历过程中遇到e>=v 不满足小于v的情况,停止i++;同理,j--的过程中遇到 e<= v 不满足大于v的情况,停止j--;
i和j交换位置,交换位置后,i++查看下一个元素,j++查看下一个元素。
直到 i 和 j 索引重合,意味着遍历结束。
? ? ? ? 实际上,按照这个逻辑走完,其实 左分区 是小于等于v的元素集合,右分区是大于等于v的元素集合。
????????如果 i 和 j 都指向了 等于v的元素,两个仍然要交换一下位置,这样就遇到大量等于v的元素的情况,也可以尽量平分这些元素。
算法思想实现:
package com.cosyit.offer.algorithms;
import java.util.Arrays;
import java.util.Random;
public class QuickSort3 {
private static void quickSort(Comparable[] a, int n) {
__quickSort(a, 0, n - 1); // a[0] - a[length-1]
}
private static void __quickSort(Comparable[] a, int l, int r) {
//设置临界条件。 obscure
if (l >= r) return;
//隔板分区
int p = partition(a, l, r);
// l 到 p-1 的分区部分 进行快速排序。
__quickSort(a, l, p - 1);
// p+1 到 r 的分区部分 进行快速排序。
__quickSort(a, p + 1, r);
}
/**
* 推举出一个元素作为隔板元素以进行分区,隔板分区后该元素将处于其顺序的位置,并返回该隔板元素的索引。
* 元素a[p]的隔板效果:左边的比隔板元素小 a[l...p-1] < arr[p],右边都比隔板元素大 a[p] < a[p+1...r]
*
* @param a 传入的数组。
* @param l 左边界元素索引。
* @param r 有边界元素索引。
* @return 隔板操作后的,隔板位置索引。
*/
private static int partition(Comparable[] a, int l, int r) {
// core 保持随机性。
//生成随机索引。 l + 随机[0 ... r - l + 1)的数
int randomIndex = l + new Random().nextInt(r - l + 1);
//和首元素交换。
swap(a, l, randomIndex);
// 1.推举出一个元素,这里我们推举我们的头部元素为隔板元素。
Comparable v = a[l];
int i = l + 1, j = r;
while (true) {
// i在运动的过程中,i <= r 防止索引越界。
while (i <= r && less(a[i], v)) i++; // i往前走不停止。
while (j >= l + 1 && less(v, a[j])) j--; // j往前走不停止。
if (i > j) break;
//都停下来了,交换元素。
swap(a, i, j);
//各自指向下一个元素,继续。
i++;
j--;
}
swap(a,l,j);
return j;
}
private static void swap(Comparable[] arr, int i, int j) {
Comparable temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
private static boolean less(Comparable a, Comparable b) {
return a.compareTo(b) < 0;
}
public static void main(String[] args) {
Integer[] arr = {6, 7, 1, 4, 3, 5, 2, 0};
quickSort(arr, arr.length);
System.out.println(Arrays.toString(arr));
}
}
改进3:以上实现中,对于大量重复的元素,会不必要的将等值的元素进行交换。为了规避这个问题,有一种经典的实现方式 --- 三路切分的快速排序 Quick Sort 3 Way。
算法思路:?
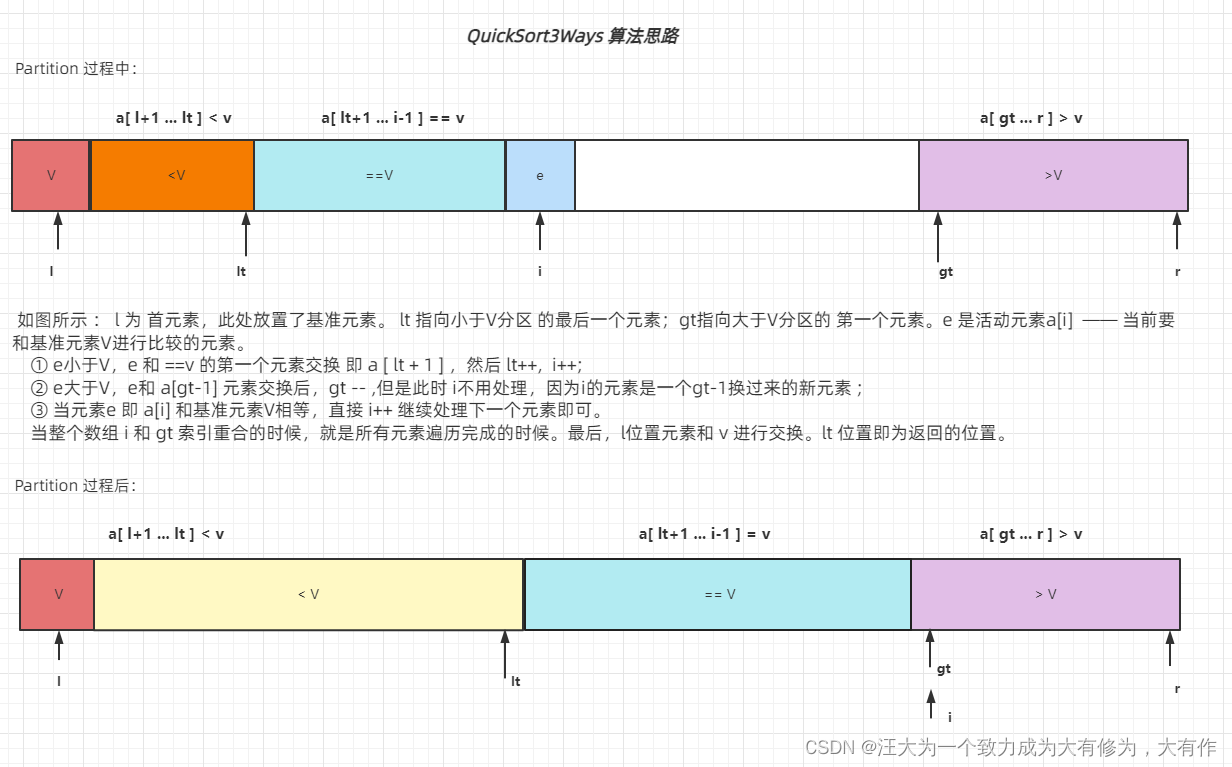
之前在切分过程中都是切分为大于基准元素V和小于基准元素V的情况,三路排序则是切分为 等于基准元素V,大于V和小于V 三种情况。
?
??????????如图所示? l 为 首元素,此处放置了基准元素。 lt 指向小于V分区 的最后一个元素;gt指向大于V分区的 第一个元素。e 是活动元素a[i]? ——?当前要和基准元素V进行比较的元素。
? ? ① e小于V,e 和 ==v 的第一个元素交换 即 a [ lt + 1 ] ,然后 lt++,? i++;
? ? ② e大于V,e和 a[gt-1] 元素交换后,gt -- ,但是此时 i不用处理,因为i的元素是一个gt-1换过来的新元素 ;
? ? ③ 当元素e 即 a[i] 和基准元素V相等,直接 i++ 继续处理下一个元素即可。
? ? 当整个数组 i 和 gt 索引重合的时候,就是所有元素遍历完成的时候。最后,l位置元素和 v 进行交换。lt 位置即为返回的位置。?
三路排序算法思想实现:
package com.cosyit.offer.algorithms;
import java.util.Arrays;
import java.util.Random;
public class QuickSort3Ways {
private static void quickSort3Ways(Comparable[] a, int l, int r) {
if(r<=l) return;
// core 保持随机性。
//生成随机索引。 l + 随机[0 ... r - l + 1)的数
int randomIndex = l + new Random().nextInt(r - l + 1);
//和首元素交换。
swap(a, l, randomIndex);
// 1.推举出一个元素,这里我们推举我们的头部元素为隔板元素。
Comparable v = a[l];
int lt = l; // a[l+1 ... lt] < v , a[l+1 ... lt]初始范围为空。
int gt = r + 1; // a[gt...r] > v ,a[gt...r] 初始范围为空。
int i = l + 1;// l为首个基准元素V,遍历元素从l+1开始。 a[lt+1...i) == v
while (i < gt) { //只要i在比较的过程中,i没有和gt碰上,就一直遍历。
int cmp = a[i].compareTo(v);
if (cmp < 0) {
swap(a, i, lt + 1);
lt++; i++;
} else if ( cmp >0) {
swap(a, i, gt - 1);
gt--;
} else {
i++;
}
}
//v和lt交换
swap(a, l, lt); lt--;
//此时, ==v 的部分已经在有序的部分,无须排序。
//排序 l...lt 的左分区。
quickSort3Ways(a, l, lt );
//排序 gt...r 的右分区。
quickSort3Ways(a, gt, r);
}
private static void swap(Comparable[] arr, int i, int j) {
Comparable temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
Integer[] arr = {6, 7, 1, 4, 3, 5, 2, 0};
quickSort3Ways(arr,0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
}
以上代码可以将和切分元素相等的元素归位,这样和v相等的元素在就不会在递归函数中处理了,在递归的函数中和v相等的元素,不会参与排序了,这样提高了效率。
?