1. 暴力匹配算法BF
在了解KMP算法前,就必须介绍串的暴力匹配算法(BF算法)
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。

如果字符匹配,i和j同时向前移动,同时还需要一个变量记录i的初始位置pos。
如果j走到了字符末尾,说明字符串匹配,返回pos即可
否则说明字符串不匹配,j退回原字符串的起始,i变成pos的下一个位置,并且更新pos的值
很容易看出,暴力匹配的算法时间复杂度为O(N2)
C++代码如下:
#include <string>
#include <iostream>
using namespace std;
/**
* @brief 字符串暴力匹配算法
*
* @param src 源字符串
* @param dst 需要匹配的字符串
* @return int 返回第一次出现要匹配的子串的位置,下标从0开始
*/
int BF(const string &src, const string &dst)
{
if (src.size() == 0 || dst.size() == 0)
{
return -1;
}
int posSrc = 0;
int posDst = 0;
while (posSrc < src.length() && posDst < dst.length())
{
if (src[posSrc] == dst[posDst])
{
posSrc++;
posDst++;
}
else
{
//回退
posSrc = posSrc - posDst + 1;
posDst = 0;
}
}
//说明匹配到最后的字符了,返回第一次出现字串的位置
if (posDst == dst.length())
{
return posSrc - posDst;
}
else
{
return -1;
}
}
int main()
{
// cout << BF("abcabcabcdabcde", "abcd") << endl;
cout << BF("abcdabcabcdabcde", "abcd") << endl;
return 0;
}
2. KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次
数以达到快速匹配的目的。
具体实现就是通过一个next数组实现,这个数组本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)
KMP算法于BF算法最大的不同点是:
匹配失败后主串的 i 并不会回退,j也不会直接回到0号位置
eg:
首先如果两个串字符匹配的话就同步向前走

BF算法i就直接回退到1位置,就回退到0位置。实际上并不需要,因为这次一定不可能匹配。
i不回退,这里的最优回退是j回退到2位置。 KMP算法关键就是找j回退到那里。
因为KMP算法本身要求i不会退。所以,需要尽量在已经匹配的主串中找到和字串匹配的部分。
j回退的位置是需要查询next数组的。
next数组定义:保存字串某个位置匹配失败后回退的位置。
next数组的下标就是匹配失败的字符在字串的位置,对应下标的值就是j需要回退的位置。
next数组求法
-
找到匹配成功部分的两个相等的真子串(不包含本身),一个以下标 0 字符开始,另一个以 j-1 下标字符结尾。
eg:
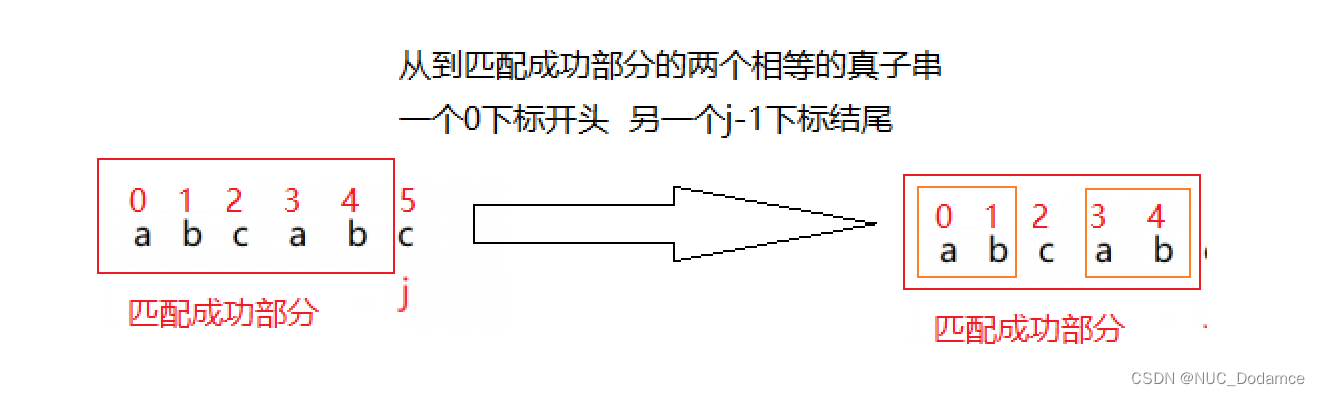
-
找到两个真字串的长度就是这位置匹配失败回退的位置。找不到两个回退位置就是0
-
不管什么数据 next[0] = -1 next[1] = 0
练习:
下标:0 1 2 3 4 5 6 7 8 9 10 11 12 13
a b a b c a b c d a b c d e
next[0]=-1 next[1]=0
next[2]:0下标对应字符为a 1下标对应字符是b 找a开头b结尾的两个真字串
next[2]=0(因为2下标前的匹配字符串找不到复合条件的两个真串)
next[3]:0下标对应字符为a ,2下标对应字符是a。找a开头a结尾的两个真字串
next[3]=1 (找到的两个真字串长度为1)
next[4]=2;next[5]=0;next[6]=1;next[7]=2;next[8]=0...
next数组为[-1 0 0 1 2 0 1 2 0 0 1 2 0 0]
-----
a b c a b c a b c a b c d a b c d e
next数组:
[-1 0 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 0]
特别注意:找两个相同的最长真字串时,第一个字串必须从0下标开始,第二个字串结尾固定是j-1位置,不能在其他位置找。
如果要实现代码,需要根据next[j]求next[j+1]的值

Java代码:
public class KMP {
public static void InitNext(String dst, int[] next) {
next[0] = -1;
next[1] = 0;
int k = 0;
for (int i = 2; i < dst.length(); i++) {
// 找str[i-1]==str[k]位置
while (k != -1 && dst.charAt(i - 1) != dst.charAt(k)) {
k = next[k];
}
next[i] = k + 1;
}
}
// 使用KMP算法返回src第一个匹配dst的位置,下标从0开始,从src的pos位置开始匹配
public static int GetSubStrPos(String src, String dst, int pos) {
if (src == null || dst == null || src.length() == 0 || dst.length() == 0)
return -1;
if (pos >= src.length() || pos < 0)
return -1;
int i = pos;// 遍历src主串
int j = 0;// 遍历dst字串
int lenSrc = src.length();
int lenDst = dst.length();
// 计算字串的next数组
int[] next = new int[lenDst];
InitNext(dst, next);
while (i < lenSrc && j < lenDst) {
if (j == -1 || src.charAt(i) == dst.charAt(j)) {
//j==-1代表第一个字符就匹配失败,i从第二个字符开始匹配,j从0开始
i++;
j++;
} else {
// i不回退
j = next[j];
}
}
if (j >= lenDst) {
// 匹配成功,返回i-j
return i - j;
} else {
return -1;
}
}
public static void main(String[] args) {
// System.out.println(GetSubStrPos("abcabcabcdabcde", "abcd", 0));
System.out.println(GetSubStrPos("abcdabcabcdabcde", "abcd", 1));
}
}
C++代码:
#include <string>
#include <iostream>
#include <vector>
#include <assert.h>
using namespace std;
//使用KMP算法返回src第一个匹配dst的位置,下标从0开始,从src的pos位置开始匹配
void InitNext(const string &dst, vector<int> &next)
{
next[0] = -1;
next[1] = 0;
int k = 0;
for (int i = 2; i < dst.size(); i++)
{
while (k != -1 && dst[i - 1] != dst[k])
{
k = next[k];
}
next[i] = k + 1;
}
}
int KMP(const string &src, const string &dst, int pos)
{
assert(pos >= 0 && pos < src.length() && src.size() > 0 && dst.size() > 0);
int i = pos;
int j = 0;
int srcSize = src.size();
int dstSize = dst.size();
vector<int> next(dst.size(), -1);
InitNext(dst, next);
while (i < srcSize && j < dstSize)
{
if (j == -1 || src[i] == dst[j])
{
i++;
j++;
}
else
{
j = next[j];
}
}
if (j == dst.size())
{
return i - j;
}
else
{
return -1;
}
}
int main()
{
// cout << KMP("abcabcabcdabcde", "abcd", 0) << endl;
// cout << KMP("abcdabcabcdabcde", "abcd", 0) << endl;
cout << KMP("abcdabcabcdabcde", "abcd", 1) << endl;
return 0;
}
KMP算法优化nextval数组
nextval数组对KMP算法的优化在于:
原KMP算法,求next数组是一个循环,需要一步一步找到str[i]==str[k]的位置。
nextval数组就是对这一步一步找str[i]==str[k]的优化。
nextval数组生成规则:
- 先根据next数组生成规则计算值这就是不匹配需要回退的位置。
- 如果当前回退的位置,正好是和当前字符一样,那么就写那个字符的nextval值。不一样就写原来的next数组的值。
