[数据结构与算法]D. AND OR and square sum(二进制位+贪心)

Problem - 1368D - Codeforces

?题意:

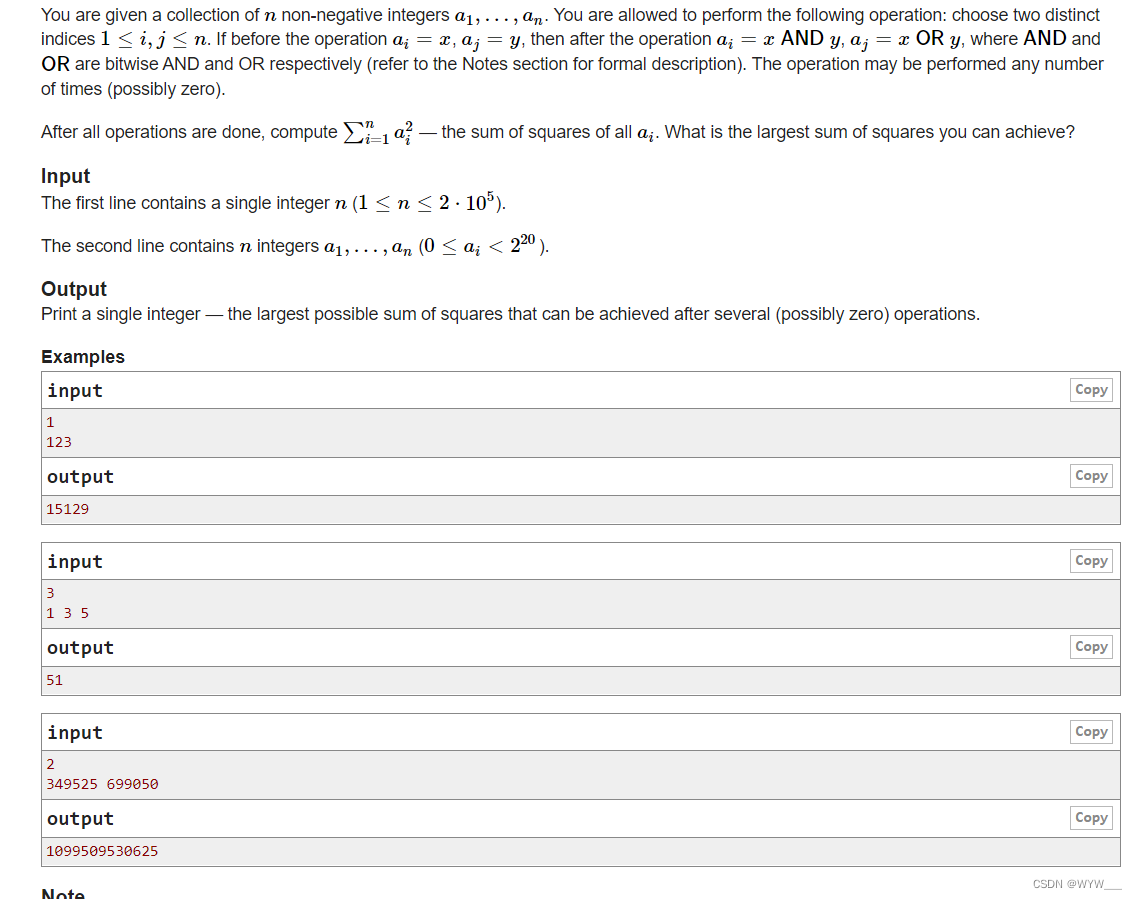
给你一个n个非负整数的集合a1,...,an。允许你进行以下操作：选择两个不同的指数1≤i,j≤n。如果在操作前ai=x，aj=y，那么在操作后ai=x AND y，aj=x OR y，其中AND和OR分别是位数的AND和OR（关于正式描述请参考注释部分）。该操作可以进行任意次数（可能为零）。

所有操作完成后，计算所有ai的平方之和。你能达到的最大平方之和是多少？

输入
第一行包含一个整数n（1≤n≤2?105）。

第二行包含n个整数a1,...,an（0≤ai<220）。

输出
打印一个整数--经过若干次（可能是零次）运算后能达到的最大可能的平方数之和。

题解:
通过一些例子比如 5:101 3:11? ?操作后为 1? 111

111 0? ? -> 0? 111

可以发现一个规律:任此此操作后 一的数量是不变的,变得只是他的位置,每次如果出现0与1的位置交换,结果都会增大

换句话来说我们可以找所有位置的一的数量,构造一些很大的数,直到,把所有的1取完

为什么构造大的数,结果就大呢,

因为这n个数的总和无论如和操?,都是不会变的

那么对于sum

2*(sum/2)*(sum/2) 和sum*sum

哪个大显而易见

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int cnt[25];
int main()
{
	int n;
	cin >> n;
	for(int i = 1;i <= n;i++)
	{
		int x;
		cin >> x;
		for(int j = 0;j < 20;j++)
		{
			if((x>>j)&1)
			{
				cnt[j]++;
			}
		}
	}
	long long sum = 0;
	for(int i = 1;i <= n;i++)
	{
		long long ans = 0;
		for(int j = 0;j  < 20;j++)
		{
			if(cnt[j])
			{
				cnt[j]--;
				ans+=(1<<j);
			}
		}
		sum += ans*ans;
	} 
	cout<<sum;
}