14天阅读挑战赛
努力是为了不平庸~
系列文章目录
第一章 算法简介
第二章 贪心算法
第三章 分治法
第四章 动态规划
目录
2.0兔子序列
意大利数学家斐波那契在《算盘全书》中描述了一个神奇的兔子序列、这就是著名的斐波那契序列。
假设第1个月有1对刚诞生的免子,第选人月讲入成熟期,第3个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,免子永不死本…那么,由1对初生兔子开始,12个月后会有多少对兔子呢?如果是N对初生的兔子开始,M月后又会有多少对兔子呢?
第1个月,兔子①没有繁殖能力,所以还是1对。
第2个月,兔子①进入成熟期,仍然是1对。
第3个月,兔子①生了1对小负2,干是这个月共有2对(1+1=2)兔子。
第4个月,兔子①又生了1对小兔③。兔子②进入成熟期。共有3对(1+2=3)兔子。
第5个月,兔子①又生了1对小兔④,兔子②也生下了1对小兔⑤。兔子③进入成熟期。共有5对(2+3=5)兔子。
第6个月,兔子①②③各生下了1对小兔。兔子④⑤进入成熟期。新生3对兔子加上原有的5对兔子,这个月共有8对(3+5=8)兔子。
…
这个数列有十分明显的特点,从第3个月开始,当月的兔子数=上月兔子数+本月新生小兔子数,而本月新生的兔子正好是上上月的兔子数,即当月的兔子数=前两月兔子之和。
F
(
n
)
=
{
1
,
n
=
1
1
,
n
=
1
F
(
n
?
1
)
+
F
(
n
?
2
)
,
n
>
2
F(n) = \begin{cases} 1 & ,n = 1 \\ 1 & ,n = 1 \\ F(n-1)+F(n-2) & ,n>2 \end{cases}
F(n)=?
?
??11F(n?1)+F(n?2)?,n=1,n=1,n>2?
以
F
(
5
)
F(5)
F(5)为例,如图:

从图可以看出,有大量的结点重复(子问题重叠),F(3)、F(2)、F(1)均重复计算多次。
2.1动态规划基础
百度百科中的解释,动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。说的很抽象,《趣学算法》中解释了动态规划的思想:其实也是一种分治思想,但与分治算法不同的是,分治算法是把原问题分解为若干子问题,自顶向下求解各子问题,合并子问题的解,从而得到原问题的解。动态规划也是把原问题分解为若干子问题,然后自底向上,先求解最小的子问题,把结果存储在表格中,再求解大的子问题时,直接从表格中查询小的子问题的解,避免重复计算,从而提高算法效率。
要应用动态规划思想去解决问题,待分析的问题需要具有如下性质
- 最优子结构
最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件,如果不具有最优子结构性质,就不可以使用动态规划解决。 - 子问题重叠
子问题重叠是指在求解子问题的过程中,有大量的子问题是重复的,那么只需要求解一次,然后把结果存储在表中,以后使用时可以直接查询,不需要再次求解。子问题重叠不是使用动态规划的必要条件,但问题存在子问题重叠更能够充分彰显动态规划的优势。
具体解题流程如下所示:
- 分析最优解的结构特征。
- 建立最优值的递归式。
- 自底向上计算最优解,并记录。
- 构造最优解。
上述的兔子序列就可以用这种方法求解,就是先求F(1)再求F(2)然后不停的求到F(n),在此就不具体叙述了。往下看另一个例子
最长的公共子序列、编辑距离、游船租赁、矩阵连乘、最优三角剖分、石子合并、0-1背包问题、最优二叉树都可以动态规划的思想,下面进行最长的公共子序列的讲解。
2.2最长的公共子序列
首先叙述解决流程,形成完整的思考流程。
首先,分析问题并想出算法的设计思路(文字叙述)。 然后,给出图解思路。 之后,编写伪代码。 最后,给出完整代码。 还有一件事,分析算法的复杂度,并思考改进思路。
2.2.1问题描述:
给定两个序列 X = { x 1 , x 2 , … , x m } X=\lbrace x_1,x_2,…,x_m\rbrace X={x1?,x2?,…,xm?}和 Y = { y 1 , y 2 , … , y n } Y=\lbrace y_1,y_2,…,y_n\rbrace Y={y1?,y2?,…,yn?}时,找出 X X X和 Y Y Y的一个最长的公共子序列。例如: X = { A , B , C , B , A , D , B } X=\lbrace A,B,C,B,A,D,B\rbrace X={A,B,C,B,A,D,B}, Y = { B , C , B , A , A , C } Y=\lbrace B,C,B,A,A,C\rbrace Y={B,C,B,A,A,C},那么最长公共子序列是 { B , C , B , A } \lbrace B,C,B,A\rbrace {B,C,B,A}。
如何找到最长公共子序列呢?如果使用暴力搜索方法,需要穷举 X X X的所有子序列,检查每个子序列是否也是 Y Y Y的子序列,记录找到的最长公共子序列。 X X X的子序列有 2 n 2^n 2n个(注意这里不要求连续,只要求递增的顺序!),因此暴力求解的方法时间复杂度为指数阶,这是我们避之不及的爆炸性时间复杂度。
2.2.2分析问题&设计思路:
这时候就需要判断能不能利用动态规划算法,分析如下,按照《趣学算法》一书中的情况讨论:
- 分析最优解的结构特征。
假设已经知道 Z k = { z 1 , z 2 , … , z k } Z_k=\lbrace z_1,z_2,…,z_k\rbrace Zk?={z1?,z2?,…,zk?}是 X m = { x 1 , x 2 , . . . , x m } X_m=\lbrace x_1,x_2,...,x_m\rbrace Xm?={x1?,x2?,...,xm?} 和 Y n = { y 1 , y 2 , y 3 , … , y n } Y_n=\lbrace y_1,y_2,y_3,…,y_n\rbrace Yn?={y1?,y2?,y3?,…,yn?}的最长公共子序列。这个假设很重要,我们都是这样假设已经知道了最优解。那么可以分3种情况讨论。
1) x m = y n = z n x_m=y_n=z_n xm?=yn?=zn?;那么 Z k ? 1 = { z 1 , z 2 , … , z k ? 1 } Z_{k-1}=\lbrace z_1,z_2,…,z_{k-1}\rbrace Zk?1?={z1?,z2?,…,zk?1?}是 X m ? 1 X_{m-1} Xm?1?和 Y n ? 1 Y_{n-1} Yn?1?的最长公共子序列。
2) x m ≠ y n , x m ≠ z n x_m\neq y_n,x_m\neq z_n xm?=yn?,xm?=zn?;我们可以把 x m x_m xm?去掉,那么 Z k Z_k Zk?是 X m ? 1 X_{m-1} Xm?1?和 Y n Y_n Yn?的最长公共子序列。
3) x m ≠ y n , y n ≠ z n x_m\neq y_n,y_n\neq z_n xm?=yn?,yn?=zn?;我们可以把 y n y_n yn?去掉,那么 Z k Z_k Zk?是 X m X_m Xm?和 Y n ? 1 Y_{n-1} Yn?1?的最长公共子序列。
看这里:这里应该是从上往下的去思考。
- 建立最优值的递归式。
设 c [ i ] [ j ] c[i][j] c[i][j]表示 X i X_i Xi?和 Y j Y_j Yj?的最长公共子序列长度。
x m = y n = z k x_m=y_n=z_k xm?=yn?=zk?;那么 c [ i ] [ j ] = c [ i ? 1 ] [ j ? 1 ] + 1 c[i][j]=c[i-1][j-1]+1 c[i][j]=c[i?1][j?1]+1
x m ≠ y n x_m\neq y_n xm?=yn?;那么我们只需要求解 X i X_i Xi?和 Y j Y_j Yj?的最长公共子序列 X i ? 1 X_{i-1} Xi?1?和 Y j Y_j Yj?的最长公共子序列,比较它们的长度哪一个更大,就取哪一个值。即 c [ i ] [ j ] = m a x { c [ i ] [ j ? 1 ] , c [ i ? 1 ] [ j ] } c[i][j]=max \lbrace c[i][j-1],c[i-1][j]\rbrace c[i][j]=max{c[i][j?1],c[i?1][j]}。
最长公共子序列长度递归式:
c
[
i
]
[
j
]
=
{
0
,
i
=
0
或
j
=
0
c
[
i
?
1
]
[
j
?
1
]
+
1
,
i
、
j
>
0
且
x
i
=
y
j
m
a
x
{
c
[
i
]
[
j
?
1
]
,
c
[
i
?
1
]
[
j
]
}
,
i
、
j
>
0
且
x
i
≠
y
j
c[i][j] = \begin{cases} 0 & ,i = 0 或j=0\\ c[i-1][j-1]+1 & ,i、j>0且x_i=y_j \\ max\lbrace c[i][j-1],c[i-1][j]\rbrace & ,i、j>0且x_i\neq y_j \end{cases}
c[i][j]=?
?
??0c[i?1][j?1]+1max{c[i][j?1],c[i?1][j]}?,i=0或j=0,i、j>0且xi?=yj?,i、j>0且xi?=yj??
- 自底向上计算最优解,并记录。
i = 1 i=1 i=1时: { x 1 } \lbrace x_1\rbrace {x1?} 和 { y 1 , y 2 , … , y n } \lbrace y_1,y_2,…,y_n\rbrace {y1?,y2?,…,yn?}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
i = 2 i=2 i=2时: { x 2 } \lbrace x_2\rbrace {x2?} 和 { y 1 , y 2 , … , y n } \lbrace y_1,y_2,…,y_n\rbrace {y1?,y2?,…,yn?}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
…
i = m i=m i=m时: { x m } \lbrace x_m\rbrace {xm?} 和 { y 1 , y 2 , … , y n } \lbrace y_1,y_2,…,y_n\rbrace {y1?,y2?,…,yn?}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
看这里:先算小的,存下来,方便后面直接调用
- 构造最优解。
上面的求解过程只是得到了最长公共子序列长度,并不知道最长公共子序列是什么,那怎么办呢?
例如,现在已经求出 c [ m ] [ n ] = 5 c[m][n]=5 c[m][n]=5,表示 X m X_m Xm?和 Y n Y_n Yn?的最长公共子序列长度是5,那么这个5是怎么得到的呢?我们可以反向追踪5是从哪里来的。根据递推式,有如下情况。
x i = y x_i=y xi?=y时: c [ i ] [ j ] = c [ i ? 1 ] [ j ? 1 ] + 1 c[i][j]= c[i-1][j-1]+1 c[i][j]=c[i?1][j?1]+1;
x i ≠ y j x_i\neq y_j xi?=yj?时: c [ i ] [ i ] = m a x { c [ i ] [ j ? 1 ] , c [ i ? 1 ] [ j ] } c[i][i]=max\lbrace c[i][j-1], c[i-1][j]\rbrace c[i][i]=max{c[i][j?1],c[i?1][j]};
那么 c [ i ] [ j ] c[i][j] c[i][j]的来源一共有3个: c [ i ] [ j ] = c [ i ? 1 ] [ j ? 1 ] + 1 , c [ i ] [ j ] = c [ i ] [ j ] , c [ i ] [ j ] = c [ i ? 1 ] [ j ] c[i][j]=c[i-1][j-1]+1,c[i][j]=c[i][j],c[i][j]=c[i-1][j] c[i][j]=c[i?1][j?1]+1,c[i][j]=c[i][j],c[i][j]=c[i?1][j]。在第3步自底向上计算最优值时,用一个辅助数组 b [ i ] [ j ] b[i][j] b[i][j]记录这3个来源:
c [ i ] [ j ] = c [ i ? 1 ] [ j ? 1 ] + 1 , b [ i ] [ j ] = 1 c[i][j]= c[i-1][j-1]+1,b[i][j]=1 c[i][j]=c[i?1][j?1]+1,b[i][j]=1;
c [ i ] [ j ] = c [ i ] [ j ? 1 ] , b [ i ] [ j ] = 2 c[i][j]=c[i][j-1],b[i][j]=2 c[i][j]=c[i][j?1],b[i][j]=2;
c [ i ] [ j ] = c [ i ? 1 ] [ j ] , b [ i ] [ j ] = 3 c[i][j]=c[i-1][j],b[i][j]=3 c[i][j]=c[i?1][j],b[i][j]=3。
这样就可以根据 b [ m ] [ n ] b[m][n] b[m][n]反向追踪最长公共子序列,当 b [ i ] [ j ] = 1 b[i][j]=1 b[i][j]=1时,输出 x i x_i xi?;当 b [ i ] [ j ] = 2 b[i][j]=2 b[i][j]=2时,追踪 c [ i ] [ j ? 1 ] c[i][j-1] c[i][j?1];当 b [ i ] [ j ] = 3 b[i][j]=3 b[i][j]=3时,追踪 c [ i ? 1 ] [ j ] , c[i-1][j], c[i?1][j],直到 i = 0 i=0 i=0或 j = 0 j=0 j=0停止。
2.2.3图解思路:
以字符串 s 1 = “ A B C A " s_1=“ABCA" s1?=“ABCA", s 2 = “ B A C D A ” s_2=“BACDA” s2?=“BACDA”为例。
(1)初始化
l
e
n
1
=
4
,
l
e
n
2
=
5
len1=4,len2=5
len1=4,len2=5,初始化
c
[
]
[
]
c[][]
c[][]第一行、第一列元素为0。
(2)填补矩阵:示例:
i
=
1
i=1
i=1时。
i
=
1
i=1
i=1;
s
1
[
0
]
s_1[0]
s1?[0]与
s
2
[
j
?
1
]
s_2[j-1]
s2?[j?1]比较,其中
j
=
1
,
2
,
3
,
…
,
l
e
n
2
j=1,2,3,…,len2
j=1,2,3,…,len2。即A与BACDA分别比较一次。
如果字符相等,
c
[
i
]
[
j
]
c[i][j]
c[i][j]取左上角数值加1,记录最优值来源
b
[
i
]
[
j
]
b[i][j]
b[i][j]=1。
如果字符不等,取左侧和上面数值中的最大值。如果左侧和上面数值相等,默认取左侧数值。如果
c
[
i
]
[
j
]
c[i][j]
c[i][j]的值来源于左侧
b
[
i
]
[
j
]
=
2
b[i][j]=2
b[i][j]=2,来源于上面
b
[
i
]
[
j
]
=
3
b[i][j]=3
b[i][j]=3。
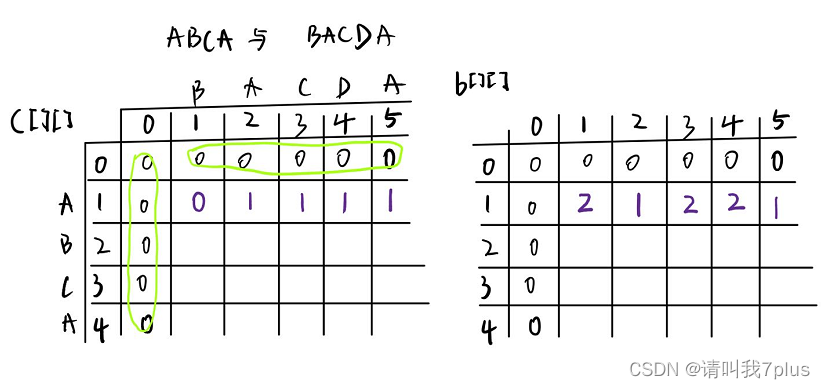
(3)继续处理
i
=
2
,
3
,
…
,
l
e
n
1
i=2,3,…,len1
i=2,3,…,len1,执行顺序(2)中的步骤。处理结果如图所示。
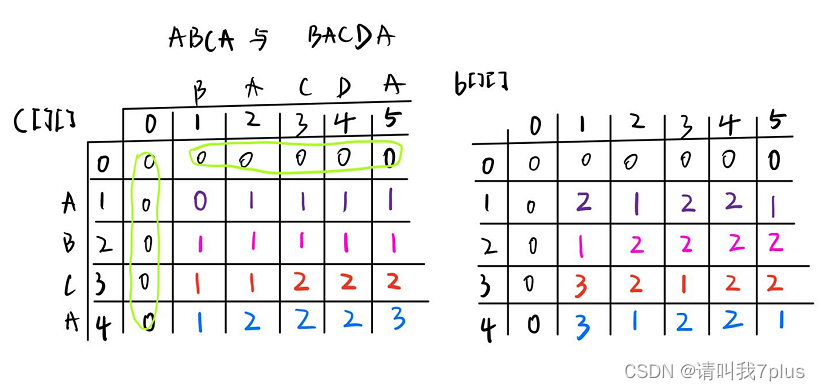
c
[
]
[
]
c[][]
c[][]右下角的值即为最长公共子序列的长度。
c
[
4
]
[
5
]
=
3
c[4][5]=3
c[4][5]=3,即字符串
s
1
=
“
A
B
C
A
"
,
s
2
=
“
B
A
C
D
A
”
s_1 =“ABCA",s_2=“BACDA”
s1?=“ABCA",s2?=“BACDA”的最长公共子序列的长度为3。
那么最长公共子序列包含哪些字符呢?
(4)构造最优解
首先读取
b
[
4
]
[
5
]
=
1
b[4][5]=1
b[4][5]=1,说明来源为1,向左上角找
b
[
3
]
[
4
]
b[3][4]
b[3][4];不停地寻找~,只有在左上角寻找时输出字符。如下:
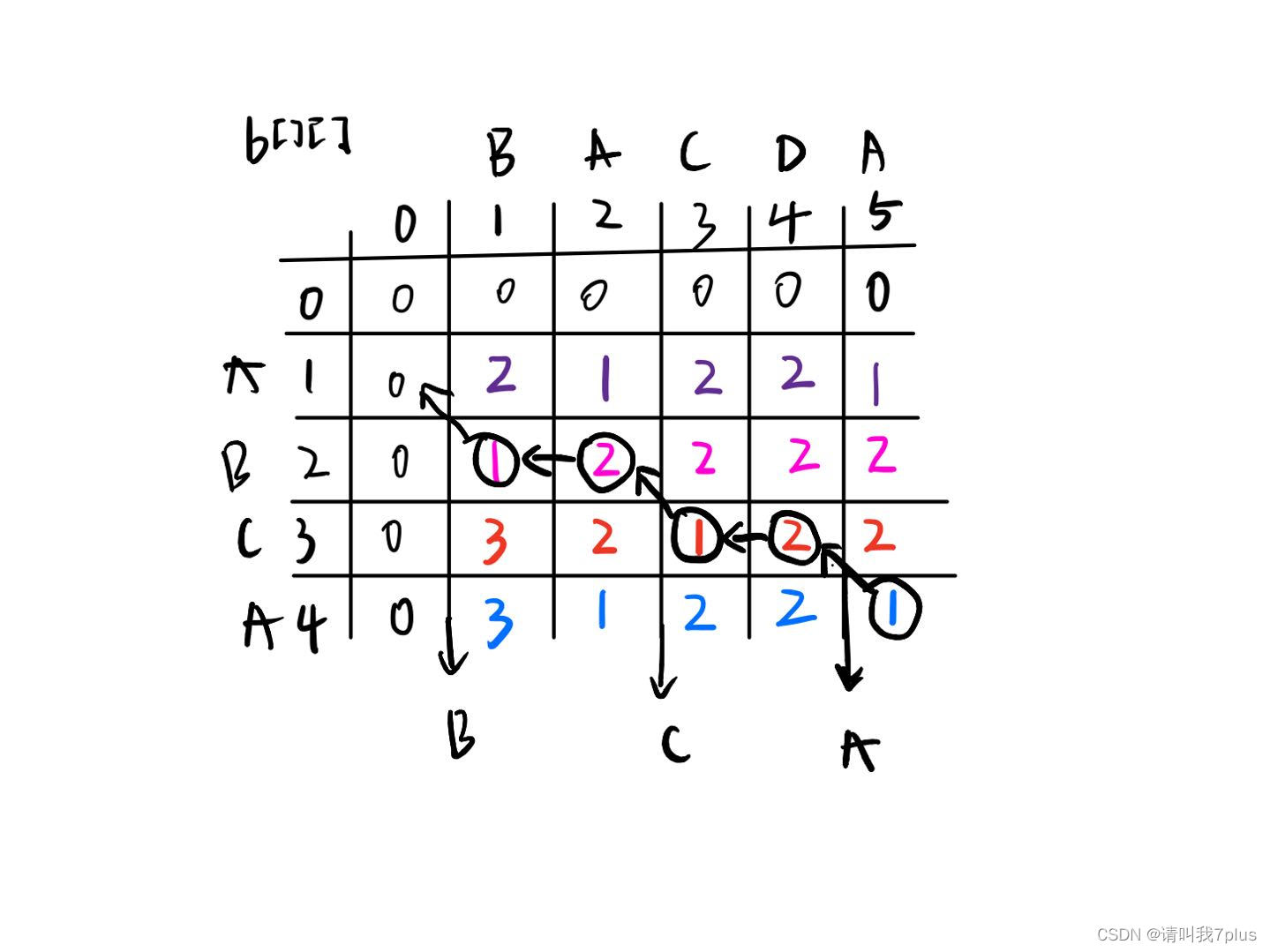
最长序列结果为BCA。
2.2.4伪代码:
- 最长公共子序列求解函数
void LCSL()
{
int i,j;
for(i=1;i<=len1;i++)//控制s1序列
{
for(j=1;j<=len2;j++)//控制s2序列
{
if(s1[i-1]==s2[j-1])
{//如果当前字符相同,则公共子序列的长度为该字符前的最长公共序列+1
c[i][j]=c[i-1][j-1] +1;
b[i][j]=1;
}
else
if(c[i][j-1] >=c[i-1][j]){
c[i][j]=c[i][j-1];
b[i][j]=2;
}
else
{
c[i][j]=c[i-1][j];
b[i][j]=3;
}
}
}
}
- 最优解输出函数
void print(int i, int j)//根据记录下来的信息构造最长公共子序列(从b[i][j]开始递推)
{
if(i==0 || j==0)return;
if(b[i][j]==1)
{
print(i-1,j-1);
cout<<s1[i-1];
}
else if(b[i][j]==2)
print(i,j-1);
else
print(i-1,j);
}
2.2.5完整代码:
#include <iostream>
#include<cstring>
using namespace std;
const int N=1002;
int c[N][N],b[N][N];
char s1[N],s2[N];
int len1,len2;
void LCSL()
{
int i,j;
for(i=1;i<=len1;i++)//控制s1序列
{
for(j=1;j<=len2;j++)//控制s2序列
{
if(s1[i-1]==s2[j-1])
{//如果当前字符相同,则公共子序列的长度为该字符前的最长公共序列+1
c[i][j]=c[i-1][j-1] +1;
b[i][j]=1;
}
else
if(c[i][j-1] >=c[i-1][j]){
c[i][j]=c[i][j-1];
b[i][j]=2;
}
else
{
c[i][j]=c[i-1][j];
b[i][j]=3;
}
}
}
}
void print(int i, int j)//根据记录下来的信息构造最长公共子序列(从b[i][j]开始递推)
{
if(i==0 || j==0)return;
if(b[i][j]==1)
{
print(i-1,j-1);
cout<<s1[i-1];
}
else if(b[i][j]==2)
print(i,j-1);
else
print(i-1,j);
}
int main()
{
int i,j;
cout<<"输入字符串s1:"<<endl;
cin>> s1;
cout<<"输入字符串s2:"<<endl;
cin>>s2;
len1 = strlen(s1);//计算两个字符串的长度
len2 = strlen(s2);
for(i=0;i<=len1;i++)
{
c[i][0]=0;//初始化第一列为0
}
for(j=0;j<=len2;j++)
{
c[0][j]=0;//初始化第一行为0
}
LCSL(); //求解最长公共子序列
cout<<"s1和s2的最长公共子序列长度是:"<<c[len1][len2]<<endl;
cout<<"s1和s2的最长公共子序列是:";
print(len1,len2);//递归构造最长公共子序列最优解
return 0;
}
运行结果:
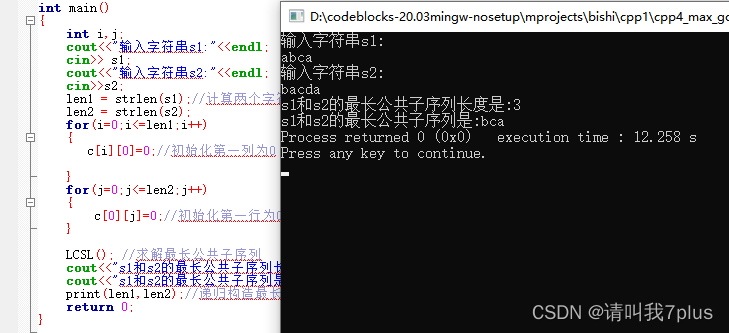
2.2.6算法复杂度分析及其改进思路:
未更新