如果去掉无向连通图G中的一条边e, 图G分裂为两个不相连的子图,那么e为图G的桥或者割边。
如果去掉无向连通图G中的一个点v及v关联的所有边,
图G分裂为两个或者两个以上不相连的子图,那么v为图G的割点。
时间戳: dfn[u]表示结点u的深度优先遍历序号
追溯点: low[u]表示结点u或者u的子孙能通过非父子边找到的dfn最小值,即通过非父子边找到最小祖先。
tarjan算法
初始时, low[u]=dfn[u],?
如果该结点的邻接点未被访问,则一直进行深度优先遍历,
回溯更新路径上所有祖先结点的low值 low[u]=min(low[u], low[v]);
如果某个结点能通过非父子边找到最小祖先, 则low[u]=min(low[u], dfn[v])
桥的判定法则: 无向边(u,v)是桥,当且仅当在搜索树上存在u的一个子节点v时,满足low[v]>dfn[u],
即孩子的low值大于自己的dfn值。
割点的判定法则: 若u不是根结点,则u是割点,当且仅当在搜索树上存在u的一个子结点v, 满足low[v]>=dfn[u];
若u是根结点,则u是割点,当且仅当在搜索树上至少存在两个子结点,并满足low[v]>=dfn[u]。
?
#include <iostream>
const int MAXN = 1000 + 2;
int n, m, head[MAXN], cnt, root;
int low[MAXN], dfn[MAXN], num;
struct Edge
{
?? ?int to;
?? ?int next;
}edges[MAXN];
void add(int u, int v)
{
?? ?edges[++cnt].next = head[u];
?? ?edges[cnt].to = v;
?? ?head[u] = cnt;
}
// 求桥
void tarjan_bridge(int u, int fa) ? // fa is u's parent
{
?? ?dfn[u] = low[u] = ++num;
?? ?for (int i = head[u]; i > 0; i = edges[i].next)
?? ?{
?? ??? ?int v = edges[i].to;
?? ??? ?if (v == fa) // v is u's father
?? ??? ??? ?continue;
?? ??? ?if (!dfn[v]) // v is unvisited
?? ??? ?{
?? ??? ??? ?tarjan_bridge(v, u);
?? ??? ??? ?// backtracking update
?? ??? ??? ?low[u] = low[u] > low[v] ? low[v] : low[u];
?? ??? ??? ?if (low[v] > dfn[u])
?? ??? ??? ??? ?std::cout << u << " --> " << v << " is one bridge edge" << std::endl;
?? ??? ?}
?? ??? ?else
?? ??? ??? ?low[u] = low[u] > dfn[v] ? dfn[v] : low[u];
?? ?}
}
// 求割点
void tarjan_artpoint(int u, int fa) ? // fa is u's parent
{
?? ?dfn[u] = low[u] = ++num;
?? ?int children = 0;
?? ?for (int i = head[u]; i > 0; i = edges[i].next)
?? ?{
?? ??? ?int v = edges[i].to;
?? ??? ?if (v == fa) // v is u's father
?? ??? ??? ?continue;
?? ??? ?if (!dfn[v]) // v is unvisited
?? ??? ?{
?? ??? ??? ?tarjan_artpoint(v, u);
?? ??? ??? ?// backtracking update
?? ??? ??? ?low[u] = low[u] > low[v] ? low[v] : low[u];
?? ??? ??? ?if (low[v] >= dfn[u])
?? ??? ??? ?{
?? ??? ??? ??? ?++children;
?? ??? ??? ??? ?if (u != root || children > 1)
?? ??? ??? ??? ??? ?std::cout << u << " is articulation point" << std::endl;
?? ??? ??? ?}
?? ??? ?}
?? ??? ?else
?? ??? ??? ?low[u] = low[u] > dfn[v] ? dfn[v] : low[u];
?? ?}
}
void init()
{
?? ?memset(head, 0, sizeof(head));
?? ?memset(low, 0, sizeof(low));
?? ?memset(dfn, 0, sizeof(dfn));
?? ?cnt = num = 0;
}
int main()
{
? ? // 输入结点数,边数
?? ?while (std::cin >> n >> m)
?? ?{
?? ??? ?init();
?? ??? ?int u, v;
?? ??? ?while (m--)
?? ??? ?{
?? ??? ??? ?std::cin >> u >> v;
?? ??? ??? ?add(u, v);
?? ??? ??? ?add(v, u);
?? ??? ?}
?? ??? ?for (int i = 1; i <= n; ++i) ?//for unconnected graph, needs to loop every vertex
?? ??? ?{
?? ??? ??? ?if (!dfn[i])
?? ??? ??? ?{
?? ??? ??? ??? ?root = i;
?? ??? ??? ??? ?//tarjan_bridge(i, 0);
?? ??? ??? ??? ?tarjan_artpoint(i, 0);
?? ??? ??? ?}
?? ??? ?}
?? ?}
?? ?return 0;
}
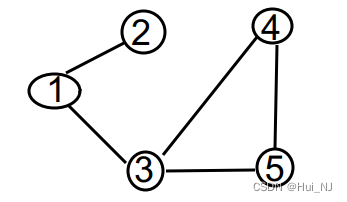
5 5
1 2
1 3
3 4
3 5
4 5
1 --> 3 is one bridge edge
1 --> 2 is one bridge edge
5 5
1 2
1 3
3 4
3 5
4 5
3 is articulation point
1 is articulation point
?