二叉树是一种最简单的树形结构,二叉树的定义是用递归的方式
二叉树具有五种基本形态:
1.空二叉树。
2.只有一个根结点。
3.根结点只有左子树。
4.根结点只有右子树。
5.根结点既有左子树又有右子树。
特点:
- 树中每个结点至多关联到两个后继结点,一个结点的关联结点数可以为0、1或2
- 一个结点关联的后继结点明确地分左右,或为其左关联结点,或为其右关联结点。
在一棵二叉树中,如果所有分支节点都有左孩子节点和右孩子节点,并且叶节点都集中在二叉树的最下一层,这样的二叉树称为满二叉树。一棵高为h,且有2^h-1个节点的二叉树称为满二叉树。
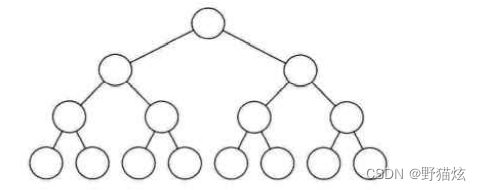
满二叉树图
若二叉树中最多只有最下面两层的节点的度数可以小于2,并且最下面一层的叶节点都依次排列在该层最左边的位置上,则这样的二叉树称为完全二叉树.
?
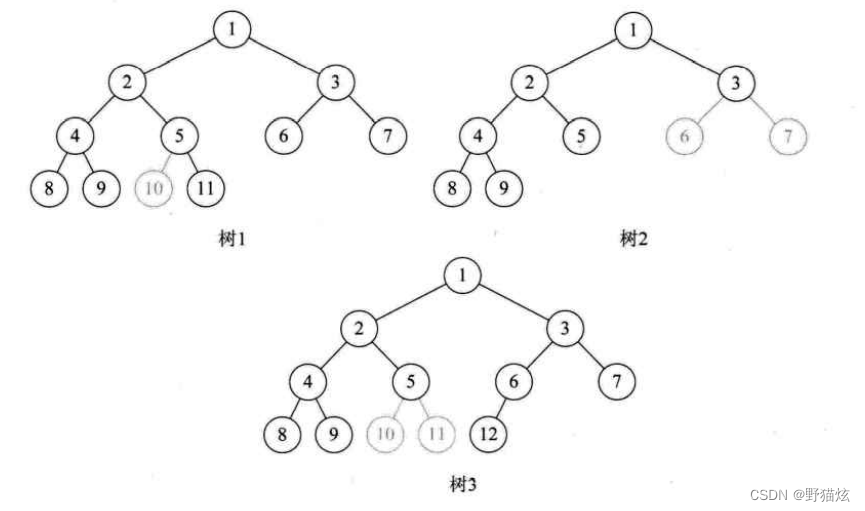
尽管它不是满二叉树,但是编号是连续的,所以它是完全二叉树。
完全二叉树图
二叉树的系统化遍历有多种可能的方式。遍历二叉树的状态搜索,以根为起始点,存在两种基本方式:
- 深度优先遍历,顺着一条路径尽可能向前探索,必要时回溯。对于二叉树,最基本的回溯情况是检查完一个叶结点。由于无路可走,只能回头。
- 宽度优先遍历,在所有路径上齐头并进。
按深度优先方式遍历一棵二叉树,需要做三件事:遍历左子树、遍历右子树和访问根结点

遍历顺序(这里假定了总是先处理左子树,否则就是6种):
按先根序遍历二叉树得到的结点序列称为其先根序列。
按后根序遍历二叉树得到的结点序列称为其后根序列。
按对称序遍历二叉树得到的结点序列称为其对称序列(中根序列)。
- 先根序遍历(按照 DLR顺序)。

- 中根序遍历(按LDR),也称对称序。
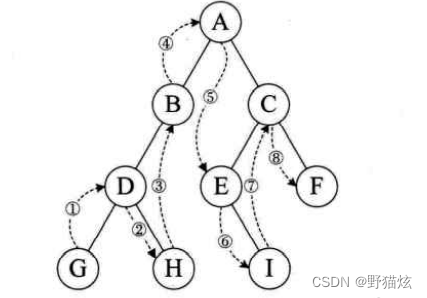
- 后根序遍历(按LRD)。
?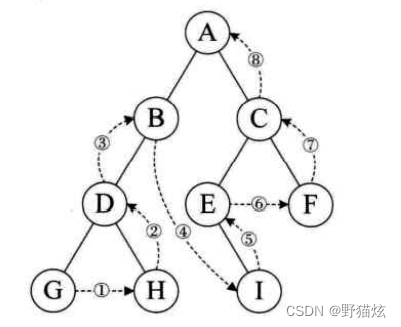
宽度优先遍历
宽度优先是按路径长度由近到远地访问结点。对二叉树做这种遍历,也就是按二叉树的层次逐层访问树中各结点,这样遍历产生的结点序列称为二叉树的层次序列。与状态空间搜索的情况一样,这种遍历不能写成一个递归过程。
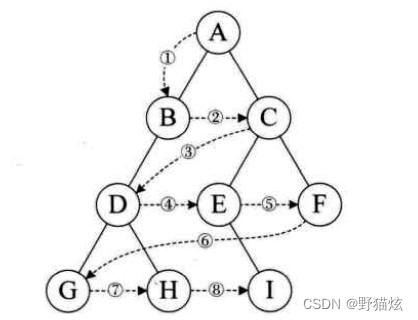
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# 用列表递归创建二叉树
def createTree(root, list_n, i):
if i < len(list_n):
if list_n[i] == 'null':
return None
else:
root = TreeNode(val=list_n[i])
root.left = createTree(root.left, list_n, 2 * i + 1)
root.right = createTree(root.right, list_n, 2 * i + 2)
return root
class Solution:
def preorderTraversal(self, root: TreeNode): # 前序
def preorder(root: TreeNode):
if not root:
return
res.append(root.val)
preorder(root.left)
preorder(root.right)
res = []
preorder(root)
return res
def inorderTraversal(self, root: TreeNode): # 中序
def inorder(root: TreeNode):
if not root:
return
inorder(root.left)
res.append(root.val)
inorder(root.right)
res = []
inorder(root)
return res
def postorderTraversal(self, root: TreeNode): # 后序
def postorder(root: TreeNode):
if not root:
return
postorder(root.left)
postorder(root.right)
res.append(root.val)
res = []
postorder(root)
return res
if __name__ == "__main__":
root = TreeNode()
# 第一种
list_n = TreeNode(
val='A', left=TreeNode(
val='B', left=TreeNode(val='D', left=TreeNode('G'), right=TreeNode('H')
)),
right=TreeNode(val='C', left=TreeNode(val='E', right=TreeNode('I')), right=TreeNode('F'))
)
# 第二种
list_n = TreeNode('A',
TreeNode('B',
TreeNode('D',
TreeNode('G'),
TreeNode('H'))),
TreeNode('C',
TreeNode('E', None,
TreeNode('I')),
TreeNode('F'))
)
s = Solution()
res_pre = s.preorderTraversal(list_n)
res_in = s.inorderTraversal(list_n)
res_post = s.postorderTraversal(list_n)
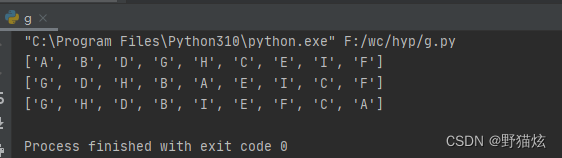
print(res_pre)
print(res_in)
print(res_post)
?
?
遍历与搜索
一棵二叉树可以看作一个状态空间:根结点对应状态空间的初始状态,父子结点链接对应状态的邻接关系。一次二叉树遍历也就是一次覆盖整个状态空间的搜索,前面所有有关状态空间搜索的方法和实现技术都可以原样移植到二叉树遍历问题中。例如,递归的搜索方法、基于栈的非递归搜索(即深度优先遍历)。基于队列的宽度优先搜索对应于这里的层次序遍历。
二叉树的list

一颗二叉树的list
['A',['B',None,None],
['C',['D',['F',None,None],
['G', None,None] ],
['E',['H', None,None],
['I', None,None]]]]
ADT BinTree:
#一个二叉树抽象数据类型
BinTree(self,data,left,right)
#构造操作,创建一个新二叉树
is_empty(self)
#判断self是否为一个空二叉树
num_nodes(self)
#求二叉树的结点个数
data(self)
#获取二叉树根存储的数据
left(self)
#获得二叉树的左子树
right(self)
#获得二叉树的右子树
set_left(self,btree)
#用btree取代原来的左子树
set_right(self,btree)
#用btree取代原来的右子树
traversal(self)
#遍历二叉树中各结点数据的迭代器
forall(self,op)
#对二叉树中的每个结点的数据执行操作op
节点由三部分组成:
- left指针:指向左子节点
- data:存储数据项
- right指针:指向右子节点?
# 实现基本操作的一组函数
def BinTree(data,left=None,right=None): #定义树节点:data为树节点存储的数据,left为左子树,right为右子树
return [data,left,right]
def is_empyt_BinTree(btree):
return btree is None
def root(btree):
return btree[0]
def left(btree):
return btree[1]
def right(btree):
return btree[2]
def set_root(btree,data):
btree[0]=data
def set_left(btree,left):
btree[1]=left
def set_right(btree,right):
btree[2] = right
eg:?
t1=BinTree(2,BinTree(4),BinTree(8))
# 相当于
t1=[2,[4,None,None],[8,None,None]]
set_left(left(t1),BinTree(5))
# 把t1的左子树的左子树换成了BinTree (5),使t1的值变成:
[2,[4,[5,None,None],None],[8,None,None]]
# 这是一棵高度为2的二叉树。list内部的嵌套层数等于树的高度。二元表达式可以很自然地映射到二叉树(运算符都是二元的):
以基本运算对象(数和变量)作为叶结点中的数据。
以运算符作为分支结点的数据:
- 其两棵子树是它的运算对象。
- 子树可以是基本运算对象,也可以是任意复杂的二元表达式。
二元表达式的遍历序列?
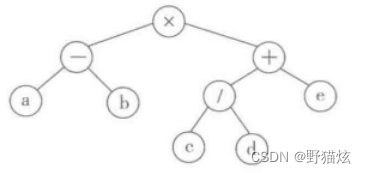
对这一表达式树的先根、后根和中根序遍历得到的符号序列:
先根序遍历得到“x - a b + / c d e”,正是该表达式的前缀表示。
后根序遍历得到的序列是“ a b - c d / e + x”,正是该表达式的后缀表示形式(即其波兰表示法的形式)。
对称序遍历得到“a - b x c / d +? e”,基本上是相应数学表达式的中缀表示,只是缺少表示计算顺序的括号(未能表达正确的计算顺序)。
三元的tuple实现二叉树结点
基本运算对象(数或变量)将直接放在空树的位置,作为基本对象。
表达式“3*(2+5)”直接映射到二叉树:
('*',(3,None,None),
('+',(2,None,None),(5,None,None)))
简化后
('*',3,('+',2,5))这种修改的表达方式,表达式由两种结构组成:
- 如果是序对(tuple),就是运算符作用于运算对象的复合表达式。
- 否则就是基本表达式,也就是数或者变量。
# 算术表达式
e1=make_prod(3,make_sum(2,5))
# 字符串表示变量,构造代数表达式
make_sum(make_prod('a',2),make_prod('b',7))
# 定义一个判别是否为基本表达式的函数
def is_basic_exp(a):
return not isinstance(a,tuple)
# 判断是否数值函数
def is_number(x):
return (isinstance(x,int) or isinstance(x,float) or
isinstance(x,complex))表达式求值
求值:简化表达式,把能计算的都计算出来。
def eval_exp(e): #求值函数,不同计算分发给具体函数处理
if is_basic_exp(e):
return e
op,a,b=e[0],eval_exp(e[1],eval_exp(e[2])) # 二叉树的所有递归处理
if op=='+':
return eval_sum(a,b)
elif op=='-':
return eval_diff(a,b)
elif op=='*':
return eval_prod(a, b)
elif op == '*':
return eval_div(a,b)
else:
raise ValueError("Unknown operator:",op)
def eval_sum(a,b): # 和式求值的函数
if is_number(a) and is_number(b):
return a+b
if is_number(a) and a==0:
return b
if is_number(b) and b==0:
return a
return make_sum(a,b)
def eval_div(a,b): #除式求值的函数
if is_number(a) and is_number(b):
return a/b
if is_number(a) and a==0:
return 0
if is_number(b) and b==1:
return a
if is_number(b) and b==0:
raise ZeroDivisionError
return make_div(a,b)来源:
《数据结构Python》
《大话数据结构》