一、题目
在一根无限长的数轴上,你站在?0?的位置。终点在?target?的位置。
你可以做一些数量的移动?numMoves?:
- 每次你可以选择向左或向右移动。
- 第?
i?次移动(从 ?i == 1?开始,到?i == numMoves?),在选择的方向上走?i?步。
给定整数?target?,返回 到达目标所需的?最小?移动次数(即最小?numMoves?)?。
二、示例
2.1> 示例 1:
【输入】 target = 2
【输出】 3
【解释】第一次移动,从 0 到 1;第二次移动,从 1 到 -1;第三次移动,从 -1 到 2 。
2.2> 示例 2:
【输入】 target = 3
【输出】 2
【解释】第一次移动,从 0 到 1;第二次移动,从 1 到 3 。
提示:
-10^9?<= target <=?10^9target != 0
三、解题思路
其实题目描述得有点不好理解。题意其实就是如下两个因素:
【移动的方向】可以向左走或者向右走
【行走的步长】第?i?步移动的距离就是?i
- 第
1步,移动距离是1;- 第
2步,移动距离是2;- ……
- 第
20步,移动距离是20;
理解了题意之后,我们就来思考一下,如何计算到达?target?所需的?最小?移动次数(numMoves)?。我们可以针对target的值做如下2种假设:
【假设1】向一个方向(向左?
or?向右)移动numMoves次,正好可以到达target。
【假设2】向两个方向(向左?and?向右)移动numMoves次,才能到达target。
“假设1”这种情况其实很好处理,我们再此就不再赘述了。主要问题是如何去处理“假设2”的这种情况,有什么好的计算办法或者规律吗??其实是有的。具体规律如下图所示:
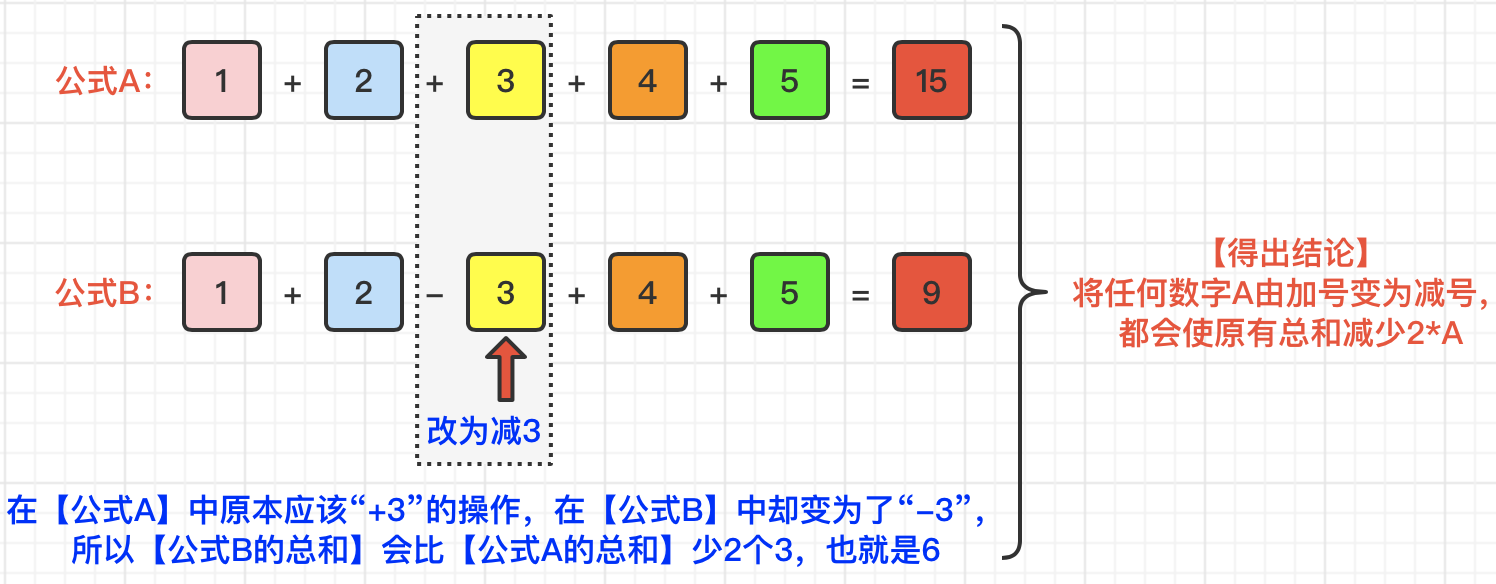
由于2*A一定是偶数,所以找到了这个规律后,我们就可以首先只朝一个方向移动(由于target会有负数的情况,所以为了统一计算方式,我们将target取绝对值即可,即:t = Math.abs(target)),只有当移动的总距离?num?的值大于等于?t?(target的绝对值),并且?num?减?t?是偶数,才表示当前情况满足题目要求,即:满足到达 target 所需的最小移动次数。具体代码实现,请见如下部分内容。
四、代码实现
class?Solution?{
????public?int?reachNumber(int?target)?{
????????int?result?=?0,?num?=?0,?t?=?Math.abs(target);?//?由于target有负数情况,为了统一计算逻辑,所以取绝对值
????????//?直到num值大于等于t,并且num减t是偶数,才结束while循环
????????while?(num?<?t?||?(num?-?t)?%?2?!=?0)?
????????????num?+=?++result;?//?num=1+2+3+4+……
????????return?result;
????}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的?点赞?&?分享?。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」