1.题目
输出1到n这n个数的全排列,要求从小到大输出
输入格式:
输入一个整数n(n<=10)
输出格式:
从小到大输出所有的全排列的数,每个数一行
输入样例:
3输出样例:
123 132 213 231 312 321
2.代码?
import java.util.*;
public class Main{
static int[] order = new int[10];
static boolean[] isMark = new boolean[10];
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
arrange(1,n);
}
public static void arrange(int k,int n)
{
int i;
if (k>n){
for (i=1;i<n;++i)
System.out.printf("%d",order[i]);
System.out.printf ("%d\n",order[n]);
return ;
}
else {
for (i=1;i<=n;i++){
if (!isMark[i]){
order[k]=i;
isMark[i]=true;
arrange(k+1,n);
order[k]=0;
isMark[i]=false;
}
}
}
}
}3.题解
3.1思路的形成
想要用递归的思路解决本题,前提是自己对回溯法与数据结构中的树有一定的了解。
3.1.1回溯法
什么是回溯?简单来说,就是不断尝试。
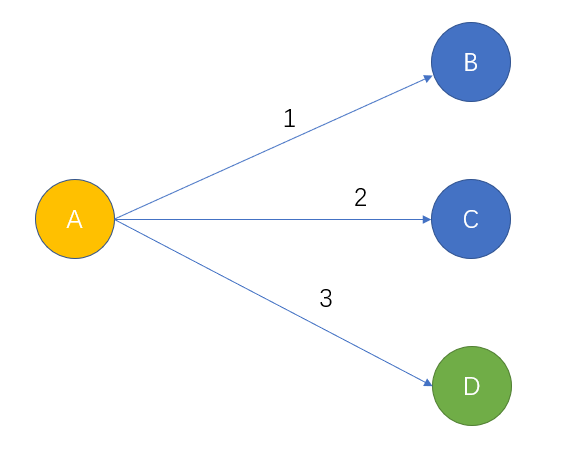
假如你是一位旅客,你想去买瓶水喝,你现在身在A点,面前有3条路,你要去看前面有没有小卖部,于是你一条路一条路地试。
你先沿路1走,到达了1的终点B,但发现B点没有,于是你原路返回到A
你再沿路2走,到达了2的终点C,但发现C点也没有,于是你原路返回到A
你再沿路3走,到达了3的终点D,发现D点有小卖部,于是你买到了水
这个过程就是回溯。
3.1.2回溯法下的数据结构
- 一个数组记录路径
- 一个数组记录路径上有没有你需要的东西
static int[] order = new int[num]; static boolean[] isMark = new boolean[num];
?3.1.3全排列的结果是棵树
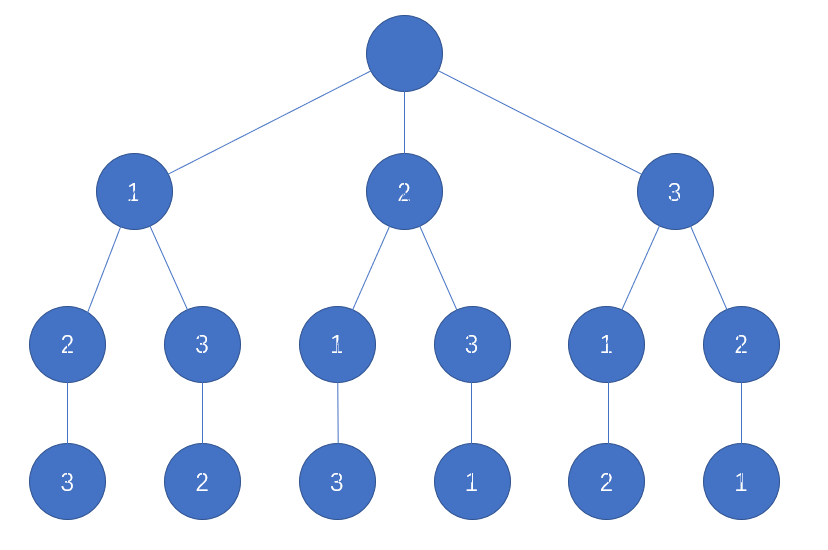
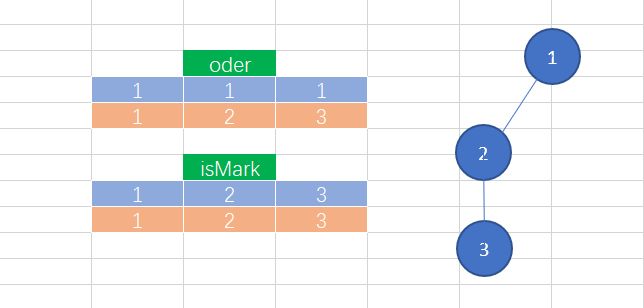
我们不妨看一看3的全排列的结果
123 132 213 231 312 321实际上它对应着一颗树
那么本题只需要从左到右输出每条路径即可,即深度遍历到叶子结点输出oder数组。?
?3.2写代码
3.2.1模拟回溯?

3.2.2递归
我们知道,递归就是要找到一个问题与其子问题的联系。
- 问题:深度遍历一棵树,依次输出到叶子结点的路径。
- 子问题:对于一个结点,深度遍历以此为根结点的子树,输出到叶子结点的路径。
对于根结点
方法化
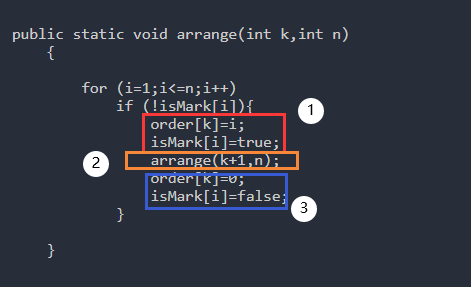
- 问题:arrange(int k,int n);
- 回溯的结构
static int[] order = new int[10]; static boolean[] isMark = new boolean[10];- 问题与子问题的关系
public static void arrange(int k,int n) { if (!isMark[i]){ order[k]=i; isMark[i]=true; arrange(k+1,n); order[k]=0; isMark[i]=false; } }- 遍历所有的子问题
public static void arrange(int k,int n) { for (i=1;i<=n;i++) if (!isMark[i]){ order[k]=i; isMark[i]=true; arrange(k+1,n); order[k]=0; isMark[i]=false; } }
- 当遍历到叶子结点后,输出一个排列
public static void arrange(int k,int n) { int i; if (k>n){ for (i=1;i<n;++i) System.out.printf("%d",order[i]); System.out.printf ("%d\n",order[n]); return ; } else { for (i=1;i<=n;i++){ if (!isMark[i]){ order[k]=i; isMark[i]=true; arrange(k+1,n); order[k]=0; isMark[i]=false; } } } }- 主函数
import java.util.*; public class Main{ static int[] order = new int[10]; static boolean[] isMark = new boolean[10]; public static void main(String[] args){ Scanner scanner = new Scanner(System.in); int n = scanner.nextInt(); arrange(1,n); } }- 完整代码(请看2.代码部分)
4.详解问题与子问题的关系?
我们可以把这部分的代码划分为3个部分
- 表示该结点遍历过,并且向对应的排列输入数据
- 递归
- 回溯
各部分的关系:
- 2的临界是输出一个排列,必然有一个最后的3进行回溯
- 2结束,3就会开始,3结束,就意味着一个arrange的结束
- 一个arrange的结束不会消除1的信息(对之前走过的路径形成记忆)
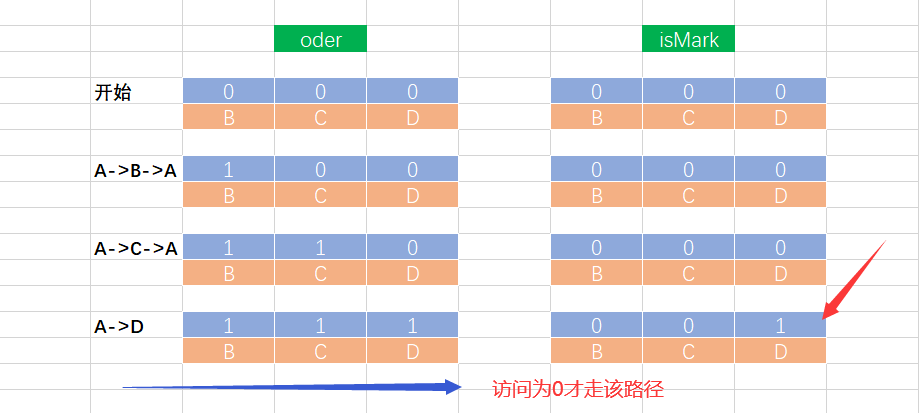
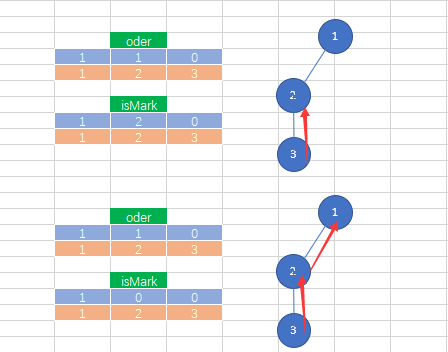
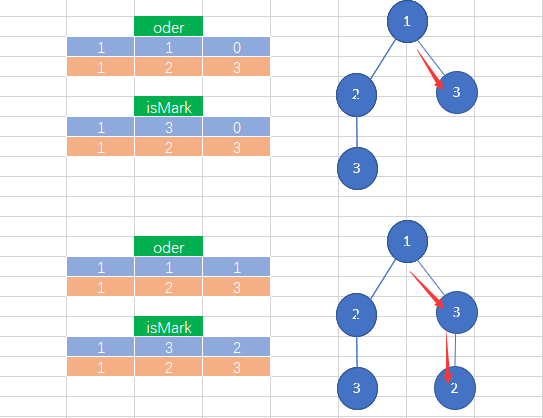
5.从叶子结点回溯的数据变化
从上图中我们可以看出,一个排列是从树的第一层到一个叶子结点
?