1、回文数
判断输入的整数是否是回文
我的一般思路:
将输入的整数转成字符串,再将这个字符串转成字符数组c,对字符数组进行遍历,如果第i个元素与第 c.length - i - 1 元素不相等,也就是通过比较首尾元素是否相同来判断是否是回文,只要有一个不相等就不是。
public boolean isPalindrome(int x) {
String s = String.valueOf(x);
char[] c = s.toCharArray();
for(int i=0;i<c.length;i++){
//比较前后元素是否相同
if(c[i]!=c[c.length-i-1]){
return false;
}
}
return true;
}进阶思路
先排除掉一定不为回文的数,比如最后一位是0且不为0,或者小于0的整数,再讨论可能为回文的情况,通过对整数除以十取余,对余数乘10,将原整数顺序颠倒,具体思路如下图

public boolean isPalindrome(int x) {
//先排除不为回文的数
if(x < 0 || (x % 10 == 0&&x!=0)){
return false;
}
//处理的余数 初值为0
int reverNum = 0;
while(x>reverNum){
reverNum = reverNum * 10 + x % 10;
x /= 10;
}
//第二种情况是当存在131这种以中间对称的数时会变成 1 和 13,所以需要做除以十取整操作
return(x == reverNum || x == reverNum / 10);
}2、最长公共前缀
求一个字符串数组的最长公共前缀
解题思路
既然是比较一个字符串数组中所有字符串的公共前缀,那么可以额外封装一个方法,用来返回两个字符串之间的公共前缀,让他们进行两两比较,最终得出所有字符串的公共前缀
public String longestCommonPrefix(String[] strs) {
//先排除非0和为空的情况
if(strs == null || strs.length == 0){
return "";
}
//取第一个数作为初始值比较
String prefix = strs[0];
//取字符串数组的总长度作为循环执行次数
int num = strs.length;
//执行循环
for(int i=1;i<num;i++){
//调用比较两个字符串公共前缀的方法
prefix = SelectMaxPro(prefix,strs[i]);
if(prefix.length() == 0){
//如果两个字符串的公共前缀为0说明没有公共前缀
//一旦有两个字符串没有公共前缀则字符串数组也没有,就跳出for循环
break;
}
if(prefix.length() == 0){
return "";
}
}
return prefix;
}
//创建查找两个字符最大公共前缀的方法
public String SelectMaxPro(String str1,String str2){
//创建一个变量作为索引,用来截取相同的前缀
int index = 0;
//找出两字符串之间最短的一个作为循环条件,防止数组越界
int minLength = Math.min(str1.length(),str2.length());
//index<minLength时 作为循环条件,并且当str1和str2对应index位置上的字符相同时index++再继续比较下一个
while(index < minLength && str1.charAt(index) == str2.charAt(index)){
index++;
}
return str1.substring(0,index);
}3、有效的括号
这里先引入栈的创建方式
栈
栈是一种先入后出的数据结构(Last In First Out, LIFO)
栈的基本实现
public class StackDemo {
public static void main(String[] args) {
//使用链表创建栈
LinkedList<Character> stack = new LinkedList<>();
//向栈中添加元素
//1、添加元素到栈顶
stack.addFirst('d');
//2、添加元素到栈底
stack.addLast('v');
//封装好的添加元素的方法
stack.push('p'); //底层直接调用addFirst()
//从栈中取数据
//当栈中元素为空时使用这种方式进行取数据会抛出NoSuchElementException异常
//1、取出栈顶元素并返回
stack.removeFirst();
//2、取出栈底元素并返回
stack.removeLast();
//3、封装好的方法返回栈顶元素
stack.pop(); //它的底层就是调用了removeFirst()
//查看栈中元素
//1、查看第一个元素
stack.getFirst();
//2、查看最后一个元素
stack.getLast();
//封装好的方法返回栈顶元素
stack.peek();
}
}题目
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
??? 左括号必须用相同类型的右括号闭合。
??? 左括号必须以正确的顺序闭合。
??? 每个右括号都有一个对应的相同类型的左括号。
public class Solution{
//创建哈希表存储键值对
Map<Character,Character> map = new HashMap<Character,Character>{{
//使用此方式在创建哈希表示就对元素进行初始化
put('(',')');put('{','}');put('[',']');put('?','?');
}};
public static boolean isValid(string s){
if(s.length() % 2 == 1){
return false;
}
//创建栈
//此处对栈初始化一个元素,防止在栈空情况下出栈抛异常
LinkedList<Character> stack = new LinkedList<Character>{{push('?')}}
char[] chars = s.toCharArray;
for(char c : chars){
if(map.containsKey(c)) stack.push(c);
//在此处进行了一个出栈的操作 满足条件就会出栈
else if(c != map.get(stack.pop())) return false;
}
return stack.size() == 1;
}
}此方法稍微有点难以理解的点在于他是何时进行的出栈,虽然他是进行一个判断栈顶元素是否等于当前元素,但当他执行完这个判断条件时就会将栈顶元素弹出,这里也可以这么理解:
//弹出的字符
char c = stack.pop()
//如果c等于弹出字符对应的值就继续向后判断否则false
if( c == map.get(c)){
continue;
}else{
return false;
}只能用于理解实际这么写会报错
4、删除有序数组中的重复项并返回处理后的数组长度

解决本题采用双指针运算,定义一个快慢指针,将快指针小于数组长度作为循环条件,如果快指针与快指针后一个位置的值相同,就说明两个元素值不相同,就将快指针的值赋给慢指针,使得不重复数据提到数组靠前的位置。但要注意双指针的初始位置都在第二位元素上,因为如果快指针在第一个位置会造成数组越界,慢指针在第一位如果前两个元素不相同,就会覆盖第一个元素。
class Solution {
public int removeDuplicates(int[] nums) {
int length = nums.length;
if(length == 0){
return 0;
}
//定义快慢指针
int fast = 1;
int low = 1;
while(fast < length){
if(nums[fast] != nums[fast - 1]){
nums[low] = nums[fast];
low++;
}
fast++;
}
return low;
}
}5、移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
对于此题可以采用基础的增强for循环实现,如果数组中的数据不等于目标值就在将这个值重新赋值给数组,否则就跳过该数据,这种方式在某种意义上也是一个双指针,只不过是Java封装好的
class Solution {
public int removeElement(int[] nums, int val) {
int index = 0;
for(int num : nums){
if(num != val){
//如果不相等就将原值重新放进数组并使指针后移
nums[index++] = num;
}
}
return index;
}
}当然也可以采用双指针的方式实现
class Solution {
public int removeElement(int[] nums, int val) {
//定义左指针
int left = 0;
//定义右指针
int right = nums.length-1;
while(left <= right){
if(nums[left] == val){
nums[left] = nums[right];
right--;
}else{
left++;
}
}
return left;
}
}6、搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
本题采用二分查找算法,可以作为简单二分查找入门题
二分查找: 定义两个指针,一个指向数组第一个位置,另一个指向数组最后一个位置,通过计算两个位置中心位置的值与目标数据进行对比,如果小于目标值,就将中间位置赋给左指针,否则赋给右指针,最后的结果一定是两指针位置相等
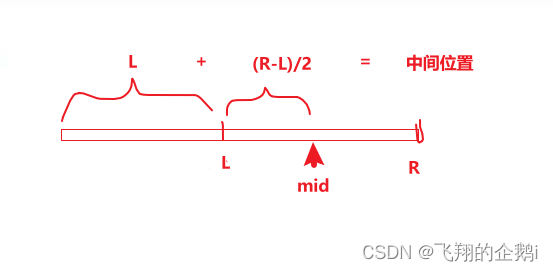 ?
?
?
class Solution {
public int searchInsert(int[] nums, int target) {
//定义左指针
int left = 0;
//定义右指针
int right = nums.length;
while(left <= right){
//设置中间位置
//这样处理的目的是防止(left+right)/2发生数组越界异常
int mid = left + (right - left) / 2;
if(nums[mid] < target){
//这里使用加一的原因是数组为递增数组,中间值已经小于目标值
//所以可以直接跳过mid值
left = mid + 1;
}else{
right = mid - 1;
}
}
return left;
}
}7、加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
class Solution {
public int[] plusOne(int[] digits) {
int n = digits.length;
for(int i = n-1 ; i >= 0; --i){
digits[i] = (digits[i] + 1) % 10;
//如果最后一个数字加一个后不为0可以提前输出,不存在增加数组大小情况
if(digits[i] != 0){
return digits;
}
}
//如果从循环中出来说明加一后数组始终为0 [9,9,9]
digits = new int[n + 1];
digits[0] = 1;
return digits;
}
}8、求x的算术平方根
给你一个非负整数
x,计算并返回?x?的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
方法一:二分查找
由于一个数的算术平方根一定小于它本身,所以可以使用二分查找来实现
class Solution {
public int mySqrt(int x) {
int index = -1;
int left = 0;
int right = x;
while(left <= right){
int mid = left + (right - left)/2;
if(mid * mid <= x){
index = mid;
left = mid + 1;
}else{
right = mid - 1;
}
}
return index;
}
}