开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据结构---动态规划 -> 正文阅读

[数据结构与算法]数据结构---动态规划

爬楼梯问题

有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

解法1

利用排列组合公式求解此题，穷举出所有的组合情况。。。。

第一步

台阶个数10阶
一次上1阶或2阶—>(求利用1和2组成10的所有排列数目)
一旦1的数目确定，2的数目也确定了
1上限100
2上限50

第二步

设置循环

        int i ;//一次爬2阶楼梯的次数
        int j ;//一次爬1阶楼梯的次数
        for (i=0;i<51;i++){
            j = 100-2*i;
        }

第三步

计算每个循环中，组合数量是多少（就是说1和2的数目确定了，求不同顺序排列的数目）
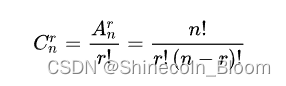
在这里插入图片描述

其中n是所有的1和2的数目，只要确定1或者2的排列，总的顺序就确定了。

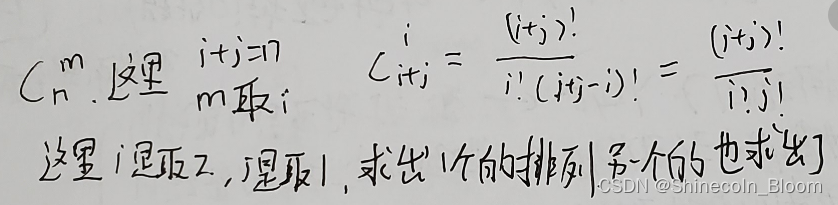
JAVA实现

//求阶乘方法
    public static long factorialUsingForLoop(int n) {
        long fact = 1;
        for (int i = 2; i <= n; i++) {
            fact = fact * i;
        }
        return fact;
    }
    /**
     * 求n阶楼梯的所有爬法
     * @param n  多少阶楼梯
     * @return
     */
    public static long sumclimbingStairs(int n){
        int i ;//一次爬2阶楼梯的次数
        int j ;//一次爬1阶楼梯的次数
        long a ;
        long b;
        long c;
        long sum=0;//累加每次排列的数目，计算总的数目
        for (i=0;i<=(n/2);i++){
            j = n-(2*i);
            //这里注意总数目是i+j不是n........
            a = factorialUsingForLoop(i+j);
            b = factorialUsingForLoop(j);//这里是Cn1(计算的1的排列)
            c = factorialUsingForLoop(i);
            sum =sum+ a/(b*c);
        }
        return sum;
    }

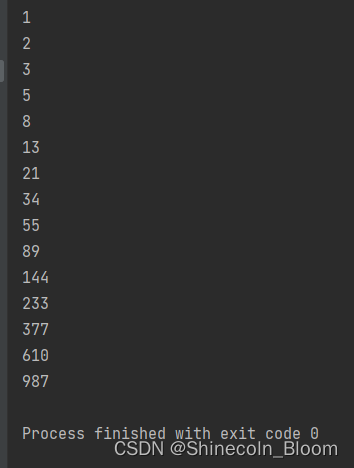
测试方法

    public static void main(String[] args) {
        System.out.println(sumclimbingStairs(1));
        System.out.println(sumclimbingStairs(2));
        System.out.println(sumclimbingStairs(3));
        System.out.println(sumclimbingStairs(4));
        System.out.println(sumclimbingStairs(5));
        System.out.println(sumclimbingStairs(6));
        System.out.println(sumclimbingStairs(7));
        System.out.println(sumclimbingStairs(8));
        System.out.println(sumclimbingStairs(9));
        System.out.println(sumclimbingStairs(10));
        System.out.println(sumclimbingStairs(11));
        System.out.println(sumclimbingStairs(12));
        System.out.println(sumclimbingStairs(13));
        System.out.println(sumclimbingStairs(14));
        System.out.println(sumclimbingStairs(15));
        //System.out.println(factorialUsingForLoop(4));
    }

在这里插入图片描述

参考

解法2

动态规划（Dynamic Programming）是一种分阶段求解决策问题的数学思想

大事化小，小事化了。。
把复杂的问题简化成规模较小的子问题，再从简单的子问题自底向上一步一步递推，最终得到复杂问题的最优解。

例子：爬10层楼梯（假设爬前九层楼梯有X种方法，爬前八层楼梯有Y种方法）

完成前九层爬的楼梯数目+再爬一层
完成前八层爬的楼梯数目+再爬两层
爬10层楼梯一共的方法数目：X+Y种方法

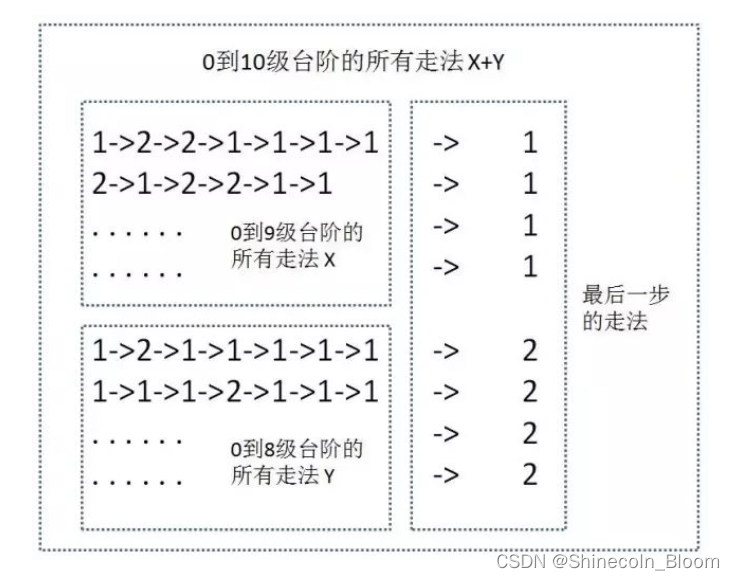
在这里插入图片描述

从0到10级台阶的走法数量=0到9级的走法数量+0到8级的走法数量。
把10级台阶的走法数量简写为F(10)，此时F(10)=F(9)+F(8)

关键在于计算F(9)和F(8)

对于F(9)和F(8)，我们有
F(9)=F(8)+F(7), F(8)=F(7)+F(6)

动态规划的思想：把一个复杂的问题分阶段进行简化,逐步简化成简单的问题。

直到递推到1级台阶和2级台阶

F(1) = 1
F(2) = 2
F(n) = F(n-1)+F(n-2)

动态规划的核心：最优子结构、边界、状态转移公式

问题建模

最优子结构

F(10)=F(9)+F(8)
所以F(9)和F(8)是F(10)的最优子结构

边界

F(1)和F(2)我们可以直接得到结果，
所以F(1)和F(2)是问题的边界

状态转移公式

F(n) = F(n-1)+F(n-2)是状态转移方程

求解问题

递归JAVA实现

边界对应递归出口，状态转移方程可以用递归实现

/**
     * 求解爬楼梯
     * @param n  楼梯的阶数
     * @return
     */
    public static int getClimbingWays(int n){
        //递归出口
        if(n<1){
            return 0;
        }
        if(n==1){
            return 1;
        }
        if(n==2){
            return 2;
        }
        //递归调用
        return getClimbingWays(n-1)+getClimbingWays(n-2);
    }

测试方法

public static void main(String[] args) {
        System.out.println(getClimbingWays(1));
        System.out.println(getClimbingWays(2));
        System.out.println(getClimbingWays(3));
        System.out.println(getClimbingWays(4));
        System.out.println(getClimbingWays(5));
        System.out.println(getClimbingWays(6));
        System.out.println(getClimbingWays(7));
        System.out.println(getClimbingWays(8));
        System.out.println(getClimbingWays(9));
        System.out.println(getClimbingWays(10));
        System.out.println(getClimbingWays(11));
        System.out.println(getClimbingWays(12));
        System.out.println(getClimbingWays(13));
        System.out.println(getClimbingWays(14));
        System.out.println(getClimbingWays(15));
    }

在这里插入图片描述

就是把复杂的问题简化成规模较小的子问题，再从简单的子问题自底向上一步一步递推，最终得到复杂问题的最优解。

计算出F(N)，就要先得到F(N-1)和F(N-2)的值。要计算F(N-1)，就要先得到F(N-2)和F(N-3)的值…以此类推，可以归纳成下面的数图:
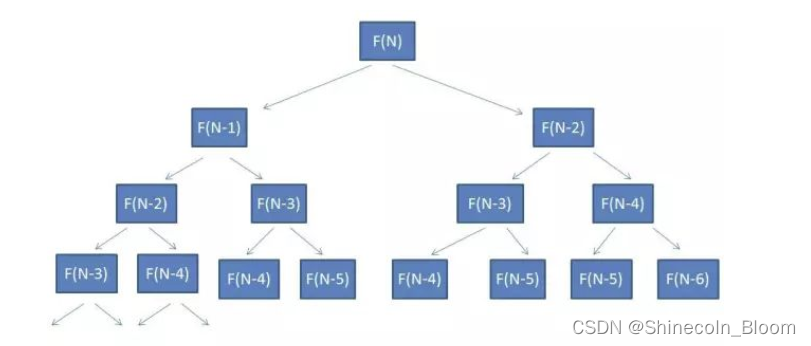
在这里插入图片描述

时间复杂度O(2ⁿ)

存在的问题，很多重复的计算。。。
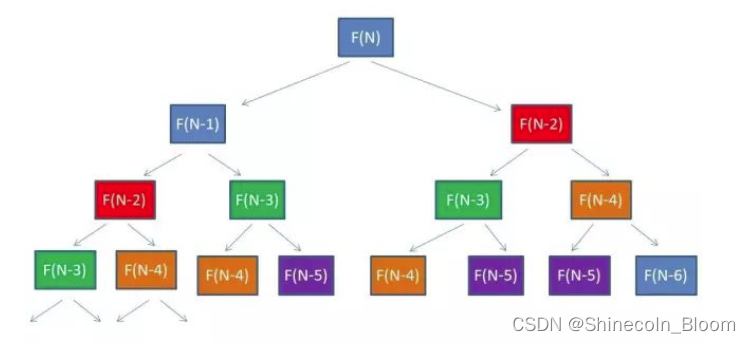
在这里插入图片描述
相同颜色是一样的传参，一样的计算。。

备忘录算法JAVA实现

针对以上问题，先创建一个哈希表，每次把不同参数的计算结果存入哈希。当遇到相同参数时，再从哈希表里取出，就不用重复计算了。

暂存计算结果

 public static int getClimbingWays(int n, HashMap<Integer,Integer> map){
        if(n<1){
            return 0;
        }
        if(n==1){
            return 1;
        }
        if(n==2){
            return 2;
        }
//        //递归调用  (改写这个)
//        return getClimbingWays(n-1)+getClimbingWays(n-2);

        /**
         * 集合map是一个备忘录。当每次需要计算F(N)的时候，
         * 会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，
         * 如果map中不存在，就计算出结果，存入备忘录中。
         */
        if(map.containsKey(n)){
            return map.get(n);
        }else {
            int value=  getClimbingWays(n-1,map)+getClimbingWays(n-2,map);
            map.put(n,value);
            return value;

        }
    }

测试方法：

public static void main(String[] args) {
        HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
        System.out.println(getClimbingWays(10,map));

    }

在这里插入图片描述

集合map是一个备忘录。当每次需要计算F(N)的时候，会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，如果map中不存在，就计算出结果，存入备忘录中。

时间复杂度：O(N)，算过一次后直接取值
空间复杂度：O(N)，因为空间存了n个值

if(map.containsKey(n)){
            System.out.println("直接取值:f("+n+")");
            return map.get(n);
        }else {
            int value=  getClimbingWays(n-1,map)+getClimbingWays(n-2,map);
            map.put(n,value);
            return value;

        }

在这里插入图片描述

解法三JAVA实现（斐波那契数列）

优化空间复杂度：自底向下，用迭代的方式推导出结果。
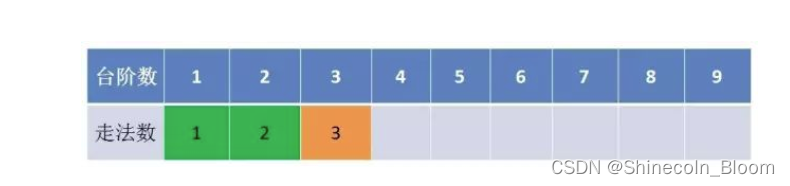
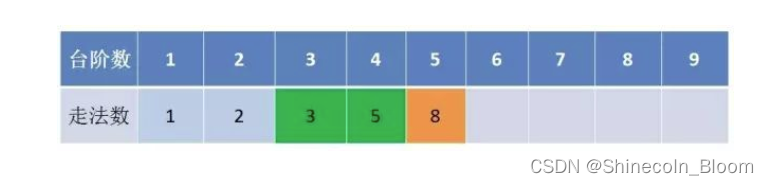
在这里插入图片描述

一次迭代过程中，只要保留之前的两个状态，就可以推导出新的状态。而不需要像备忘录算法那样保留全部的子状态。
优化空间复杂度
起其实这就是一个斐波那契数列

 /**
     * 爬楼梯
     * @param n 楼梯数目
     * @return
     */
    public static int getClimbingWays(int n){
        if(n<1){
            return 0;
        }
        if(n==1){
            return 1;
        }
        if(n==2){
            return 2;
        }
        int a = 1;
        int b = 2;
        int temp = 0;

        //自底向上---斐波那契数列
        for (int i=3;i<=n;i++){
            temp = a+b;
            a = b;
            b = temp;
        }
        return temp;
    }

测试方法：

    public static void main(String[] args) {
        for (int i =1;i<16;i++){
            System.out.println(getClimbingWays(i));
        }
    }

在这里插入图片描述

时间复杂度：O(n)
空间复杂度O(1)
迭代过程中只需保留两个临时变量a和b，分别代表了上一次和上上次迭代的结果。为了便于理解，我引入了temp变量。temp代表了当前迭代的结果值

国王和金矿

很久很久以前，有一位国王拥有5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人人数也不同。例如有的金矿储量是500kg黄金，需要5个工人来挖掘；有的金矿储量是200kg黄金，需要3个工人来挖掘……如果参与挖矿的工人的总数是10。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半的金矿。要求用程序求出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿
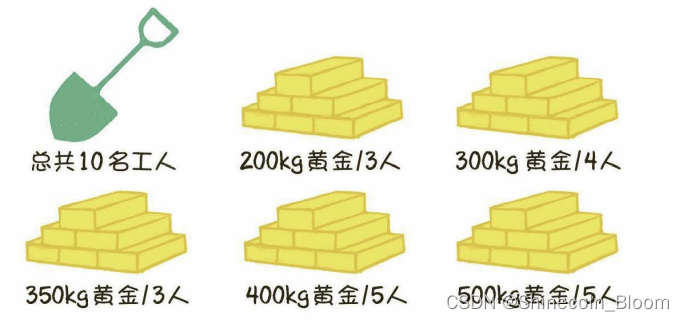
在这里插入图片描述

这是一个典型的动态规划题目，和著名的“背包问题”类似。

动态规划，就是把复杂的问题简化成规模较小的子问题，再从简单的子问题自底向上一步一步递推，最终得到复杂问题的最优解。

一个错误的解法

使用贪心算法
按照金矿的性价比从高到低进行排序，优先选择性价比最高的金矿来挖掘，然后是性价比第2的……
在这里插入图片描述
总工人10，挖掘了第一名和第二名的金矿后，剩下的2人就没法挖掘其他金矿了。
总收益：350+500=850.

局部情况下是最优解，但是在整体上却未必是最优的。

如果我放弃性价比最高的350kg黄金/3人的金矿，选择500kg黄金/5人和400kg黄金/5人的金矿，加起来收益是900kg。

排列组合解法

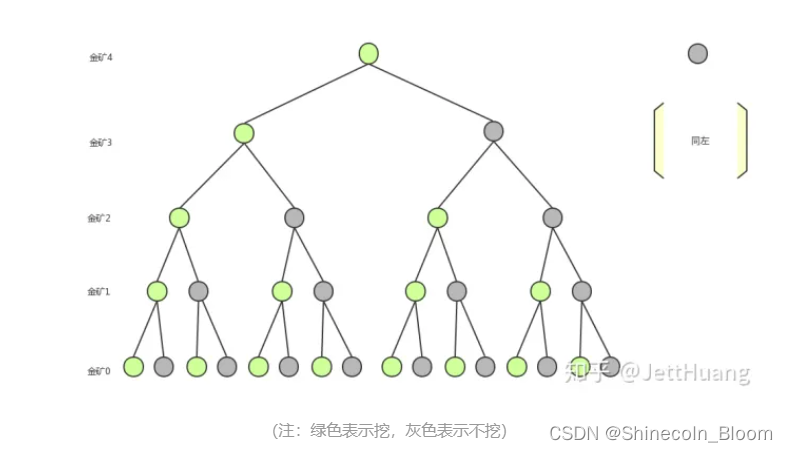
每一座金矿都有挖与不挖两种选择，如果有N座金矿，排列组合起来就有2^N种选择。对所有可能性做遍历，排除那些使用工人数超过10的选择，在剩下的选择里找出获得金币数最多的选择。

图片参考：图片源

第一步

每个金矿要么挖要么不挖，共有2⁵组合方法。枚举这些组合。
在这里插入图片描述

//取名字
    public static String name(int i){
        return (String)"temp"+i;
    }
    public static int[][] miningGold(int[] array){
        int num = 0;
        int[] temp;
        Map<String, int[] > map = new HashMap<String, int[]>();
        int [][] result = new int[32][5];
        for (int i = 0;i<2;i++){
            array[0]=i;
            for (int j =0;j<2;j++){
                array[1]=j;
                for (int k=0;k<2;k++){
                    array[2]=k;
                    for (int l=0;l<2;l++){
                        array[3] = l;
                        for (int m=0;m<2;m++){
                            array[4]=m;
                            //给变量取不同名字,用map映射
                            map.put(name(num), new int[5]);
                            /**
                             * 不能直接,result[num]=array;这里result[num]存的是array的引用。。。
                             * 一旦array变，result[num]也变了。。。。。
                             * 需要开辟不同的存储空间。。。
                             */
                            map.get(name(num))[0]=array[0];
                            map.get(name(num))[1]=array[1];
                            map.get(name(num))[2]=array[2];
                            map.get(name(num))[3]=array[3];
                            map.get(name(num))[4]=array[4];
                            result[num]=map.get(name(num));
                            num++;
                        }
                    }
                }
            }
        }
        return result;
    }

测试函数

public static void main(String[] args) {
        int[] array = new int[5];
        int[][] result ;
        result=miningGold(array);

//        //打印二维数组
//        for (int i=0;i<result.length;i++){
//            for (int j =0;j<result[i].length;j++){
//                System.out.print(result[i][j]);
//            }
//            System.out.println();
//        }

        int []G=new int[]{200,300,350,400,500};
        int []P=new int[]{3,4,3,5,5};

        //打印二维数组（所有挖掘情况）
        System.out.println("每个金矿要么挖要么不挖，共有2的5次方个组合方法。枚举这些组合结果如下： ");
        for (int i=0;i<result.length;i++){
            for (int j =0;j<result[i].length;j++){
                System.out.print(result[i][j]+"   ");
            }
            System.out.println();
        }

        System.out.println("-----------");
        }

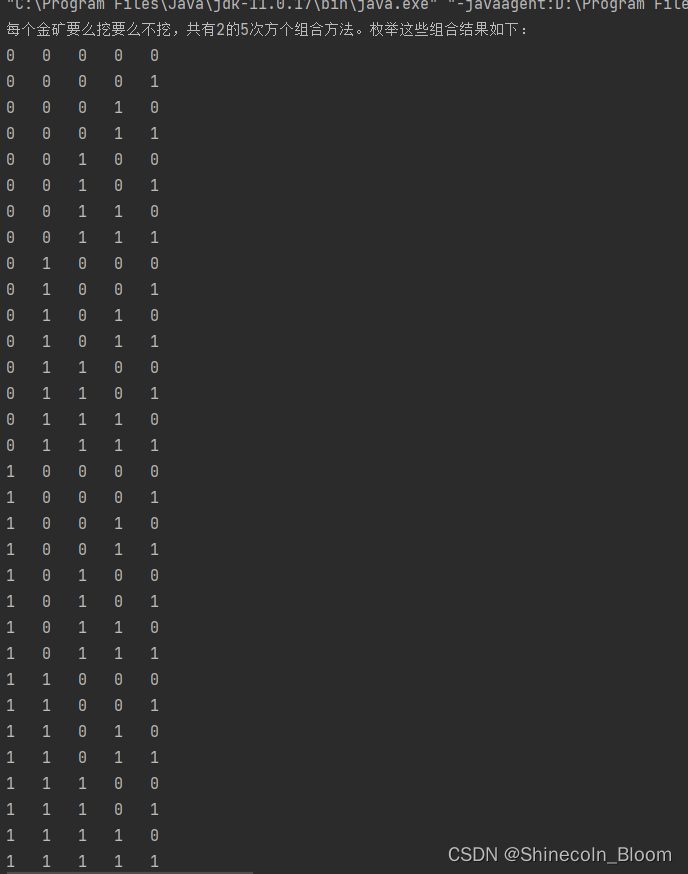
在这里插入图片描述

第二步

对所有的排列情况筛选，筛选条件是总人数10限制

在测试方法中：

System.out.println("满足总人数限制10的组合如下： ");
        int [][] realResult = new int[32][5];
        //筛选满足人数条件的情况
        int sumpeople = 10;//注意每次新的i开始得重置......
        for (int i=0;i<result.length;i++){
            for (int j=0;j<result[i].length;j++){
                sumpeople = sumpeople-P[j]*result[i][j];
                //条件为小于0
                if(sumpeople<0){
                    break;
                }
                realResult[i][j] = result[i][j];
                System.out.print(realResult[i][j]+"   ");
            }
            System.out.println();
            sumpeople=10;
        }

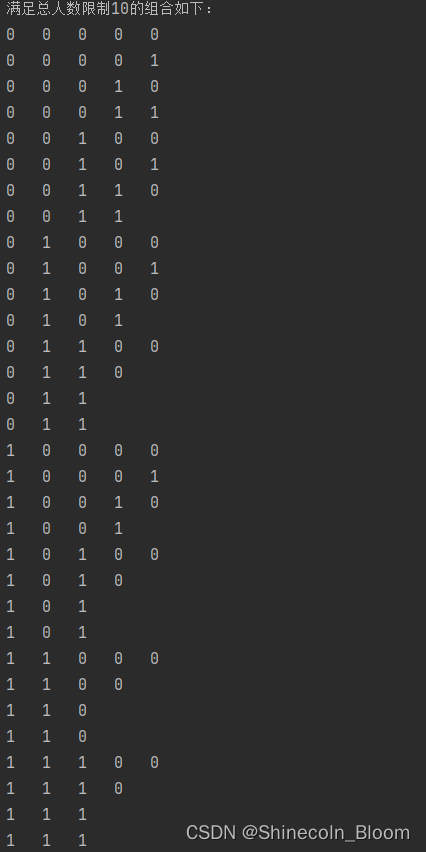
在这里插入图片描述

第三步

依据限制得出的组合，计算总金额

测试方法中：

System.out.println("再满足人数限制的情况下，所有情况的获利如下： ");
        int [][] realResultMoney = new int[32][5];
        int totalMoney = 0;
        int maxMoney = 0;
        //计算最大的获利
        for (int i=0;i<realResult.length;i++){
            for (int j =0;j<realResult[i].length;j++){
                realResultMoney[i][j]=realResult[i][j]*G[j];
                System.out.print(realResultMoney[i][j]+"  ");
                totalMoney += realResultMoney[i][j];
            }
            if(maxMoney<totalMoney){
                maxMoney = totalMoney;
            }
            totalMoney = 0;
            System.out.println();
        }
        System.out.println("最大获利为：" +maxMoney);

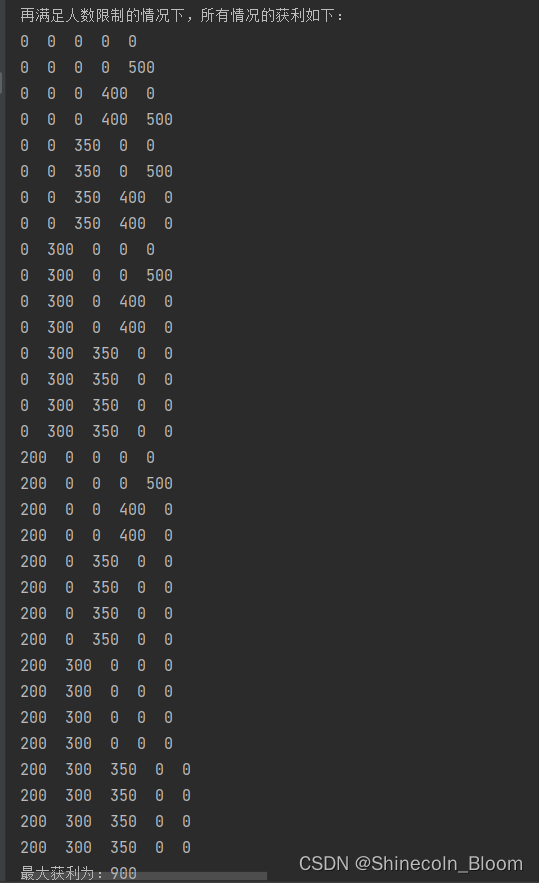
在这里插入图片描述

小BUG

在写代码的时候，不能直接,result[num]=array;这里result[num]存的是array的引用。。。
一旦array变，result[num]也变了。。。。。
需要开辟不同的存储空间。。。
这里利用哈希map

Map<String, int[] > map = new HashMap<String, int[]>();
map.put(name(num), new int[5]);
map.get(name(num))[0]=array[0];
map.get(name(num))[1]=array[1];
map.get(name(num))[2]=array[2];
map.get(name(num))[3]=array[3];
map.get(name(num))[4]=array[4];

存在的问题：时间复杂度为O(2ⁿ)

动态规划

动态规划建模核心问题：最优子结构、边界、状态转移方程。

问题建模

最优子结构

4个金矿，10个工人时的最佳选择（350kg/3人这个金矿不挖）
4个金矿，7个工人时的最佳选择（350kg/3人这个金矿挖）

究竟哪一种最优子结构可以通向全局最优解?
那就要看10个工人在前4个金矿的收益，和7个工人在前4个金矿的收益+最后一个金矿的收益谁大谁小了。

然后可以把：4个金矿，10个工人&4个金矿，7个工人再做同样的子结构。。

在这里插入图片描述

把问题一分为二，二分为四，一直把问题简化成在0个金矿或0个工人时的最优选择，这个收益结果显然是0，也就是问题的边界。

状态转移方程

F(5,10)=Max(F(4,10),F(4,10-P[4])+G(4))，n>=1且w>p[n-1]（金矿还有，且人手够）

金矿数量设为N，其中N=5
工人数设为w，其中w=10
金矿的黄金量设为数组G [ ]，其中G[400,500,200,300,350]
金矿的用工量设为数组P [ ]，其中P[5,5,3,4,3]
设F(n，w)为n个金矿、w个工人时的最优收益函数

边界

把问题一分为二，二分为四，一直把问题简化成在0个金矿或0个工人时的最优选择，这个收益结果显然是0，也就是问题的边界。

F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）
F(n,w)=F(n-1,w)，n>=1且w<p[n-1]（还有金矿，但是所剩工人不够挖掘当前金矿，就查看下一座金矿挖掘的话，人手够不够）
正常情况如下：
F(n,w)=Max(F(n-1,w),F(n-1,w-P[n-1])+G(n-1))，n>=1且w>p[n-1]（金矿还有，且人手够）

求解问题

递归JAVA实现

 /**
     * 递归解决挖金矿问题
     * @param w   工人数目
     * @param n   可以选择的金矿数目
     * @param P   金矿开采所需的工人数量
     * @param G   金矿储量
     * @return
     */
    public static int getBestGoldMining(int w,int n,int[] P,int[]G){
        //F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）
        if(w==0||n==0){
            return 0;
        }
        //F(n,w)=F(n-1,w)，n>=1且w<p[n-1]
        // （还有金矿，但是所剩工人不够挖掘当前金矿，就查看下一座金矿挖掘的话，人手够不够）
        //n-1的原因是数组P下标从0开始。。
        if(w<P[n-1]){
            return getBestGoldMining(w,n-1,P,G);
        }
        //其中第n座金矿对应的金矿数目是G[n-1],需要的人数是P[n-1]
        return Math.max(getBestGoldMining(w,n-1,P,G),getBestGoldMining(w-P[n-1],n-1,P,G)+G[n-1]);
    }

测试方法：

 public static void main(String[] args) {
        int w = 10;
        int[] p ={5,5,3,4,3};
        int[] g = {400,500,200,300,350};
        System.out.println("最佳收益： "+getBestGoldMining(w,g.length,p,g));
    }

在这里插入图片描述
全局问题经过简化，会拆解成两个子结构；两个子结构再次简化，会拆解成4个更小的子结构……就像下图一样。

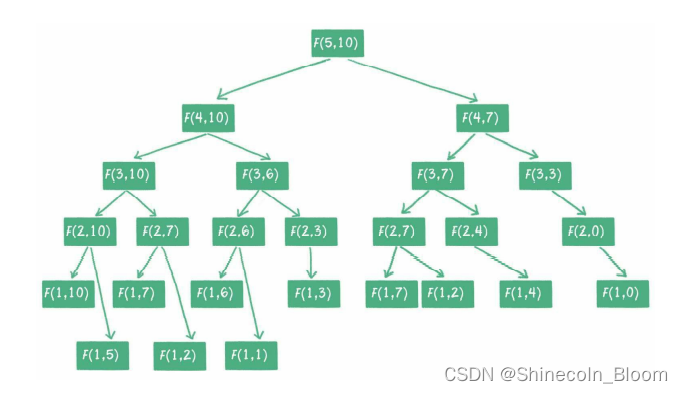
在这里插入图片描述

时间复杂度就是O(2ⁿ)

备忘录算法JAVA实现

递归调用存在的问题：递归之所以低效的根本原因，那就是递归做了许多重复的计算
递归的执行流程类似于一颗高度为N的二叉树
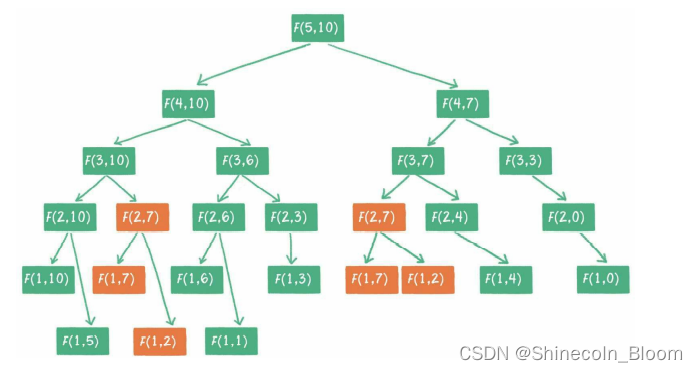
在这里插入图片描述
红色的方法调用是重复

当金矿数量为5时，重复调用的问题还不太明显，当金矿数量越多，递归层次越深，重复调用也就越来越多，这些无谓的调用必然会降低程序的性能

在简单递归的基础上增加一个HashMap备忘录，用来存储中间结果。HashMap的Key是一个包含金矿数N和工人数W的对象，Value是最优选择获得的黄金数

自底向上求解

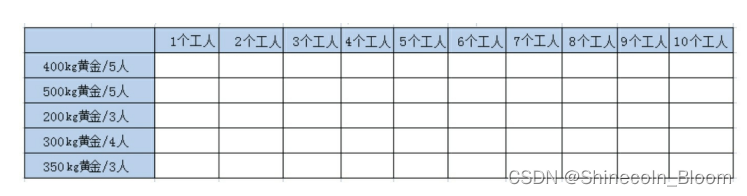
在这里插入图片描述

表格最左侧代表不同的金矿选择范围，从上到下，每多增加1行，就代表多1个金矿可供选择，也就是F( n , w)函数中的n值。
表格的最上方代表工人数量，从1个工人到10个工人，也就是F ( n , w)函数中的w值。
其余空白的格子，都是等待填写的，代表当给出n个金矿、w个工人时的最优收益，也就是
F ( n , w )的值。

例如：下图中绿色的这个格子里，应该填充的是在有5个工人的情况下，在前3个金矿可供选择时，最优的黄金收益。
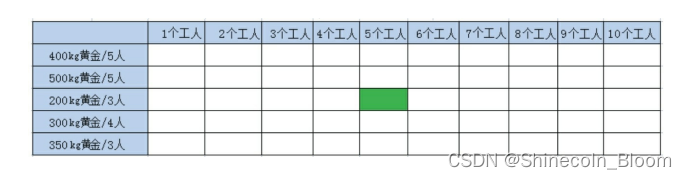
在这里插入图片描述

从第1行第1列开始，尝试把空白的格子一一填满，填充的依据就是状态转移方程式。
动态规划自底向上的求解过程如下：

于第1行的前4个格子，由于w<p[n-1]，对应的状态转移方程式如下

F(n,w)=F(n-1,w)，n>=1且w<p[n-1]（还有金矿，但是所剩工人不够挖掘当前金矿，就查看下一座金矿挖掘的话，人手够不够）
F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）

F(1，1)=F(1-1，1)=F(0，1)=0
F(1，2)=F(1-1，2)=F(0，2)=0
F(1，3)=F(1-1，3)=F(0，3)=0
F(1，4)=F(1-1，4)=F(0，4)=0
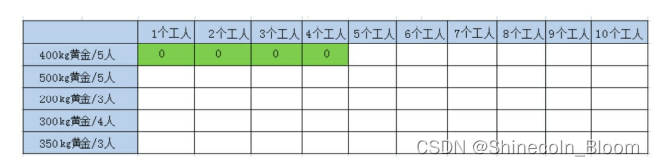
在这里插入图片描述
第1行的后6个格子，由于w>=p[n-1]，对应的状态转移方程式如下

F(n,w)=Max(F(n-1,w),F(n-1,w-P[n-1])+G(n-1))，n>=1且w>p[n-1]（金矿还有，且人手够）
F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）

F(1，5) = Max(F(1-1,5)，F(1-1,5-5)+400)=Max(F(0,5)，F(0,0)+400)=Max(0，400)=400
F(1，6) = Max(F(1-1,6)，F(1-1,6-5)+400)=Max(F(0,6)，F(0,1)+400)=Max(0，400)=400
F(1，7) = Max(F(1-1,7)，F(1-1,7-5)+400)=Max(F(0,7)，F(0,2)+400)=Max(0，400)=400
F(1，8) = Max(F(1-1,8)，F(1-1,8-5)+400)=Max(F(0,8)，F(0,3)+400)=Max(0，400)=400
F(1，9) = Max(F(1-1,9)，F(1-1,9-5)+400)=Max(F(0,9)，F(0,4)+400)=Max(0，400)=400
F(1，10) = Max(F(1-1,10)，F(1-1,10-5)+400)=Max(F(0,10)，F(0,5)+400)=Max(0，400)=400
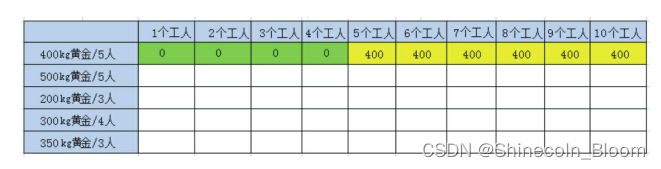
在这里插入图片描述
对于第2行的前4个格子，和之前一样,对应的状态转移方程式如下

F(n,w)=F(n-1,w)，n>=1且w<p[n-1]（还有金矿，但是所剩工人不够挖掘当前金矿，就查看下一座金矿挖掘的话，人手够不够）
F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）

F(2，1)=F(2-1，1)=F(1-1，1)=0
F(2，2)=F(2-1，2)=F(1-1，2)=0
F(2，3)=F(2-1，3)=F(1-1，3)=0
F(2，4)=F(2-1，4)=F(1-1，4)=0
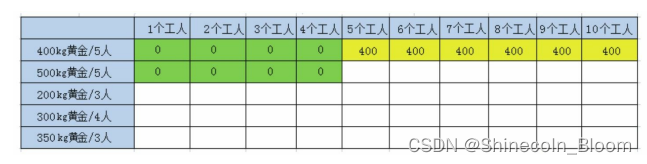
在这里插入图片描述
第2行后6个格子，同理第一行后6个格子。状态转移方程如下

F(n,w)=Max(F(n-1,w),F(n-1,w-P[n-1])+G(n-1))，n>=1且w>p[n-1]（金矿还有，且人手够）
F(n,w)=0，n=0或w=0（当金矿数目为0或者没有工人了，则不能再产生收益了，达到问题边界）

F(2，5) = Max(F(2-1，5)，F(2-1，5-5)+500）=Max(F(1，5)，F(1，0)+500)=Max(400，500)=500
F(2，6) = Max(F(2-1，6)，F(2-1，6-5)+500）=Max(F(1，6)，F(1，1)+500)=Max(400，500)=500
F(2，7) =Max(F(2-1，7)，F(2-1，7-5)+500）=Max(F(1，7)，F(1，2)+500)=Max(400，500)=500
F(2，8) = Max(F(2-1，8)，F(2-1，8-5)+500）=Max(F(1，8)，F(1，3)+500)=Max(400，500)=500
F(2，9) = Max(F(2-1，9)，F(2-1，9-5)+500）=Max(F(1，9)，F(1，4)+500)=Max(400，500)=500
F(2，10)=Max(F(2-1，10)，F(2-1，10-5)+500）=Max(F(1，10)，F(1，5)+500)
=Max(400，400+500)=900
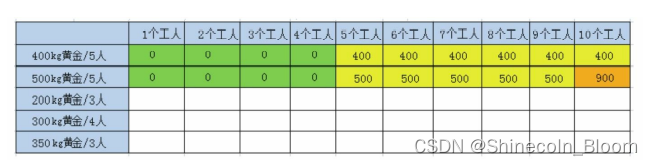
在这里插入图片描述
第三行：

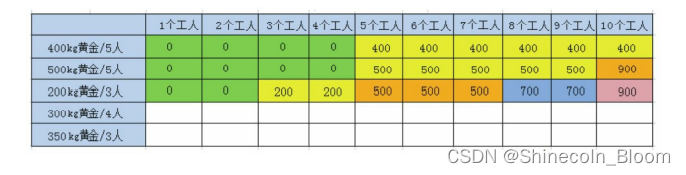
第四行

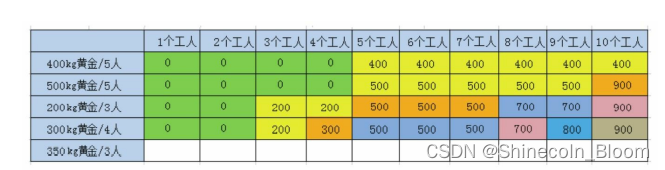
第5行

/**
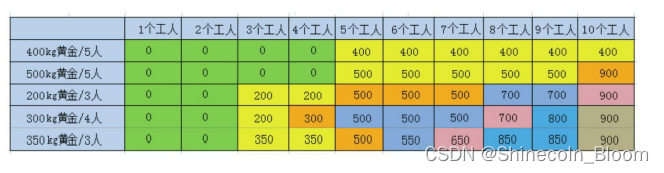
     * 动态规划自底向上求解（表格）
     * @param w   工人数量  题目里面是10个工人
     * @param P   金矿开采所需的工人数量
     * @param G   金矿储量
     * @return
     */
    public static int[][] getBestGoldMining(int w,int[]P,int[]G){
        //创建表格
        int[][] resultTable = new int[G.length+1][w+1];
        //自底向上填充表格
        //外层循环一次是一行(不同的金矿数目)
        //内存循环一次是一列（不同的工人数目）
        //下一行依靠上一行的数据完成。。。。。
        for (int i=1;i<=G.length;i++){
            for (int j=1;j<=w;j++){
                //当前工人数目w不足以开采当前第i金矿（需要P[i-1]个工人）
                //F(n,w)=F(n-1,w)，n>=1且w<p[n-1]（还有金矿，但是所剩工人不够挖掘当前金矿，就查看下一座金矿挖掘的话，人手够不够）
//                if(i==1&j<P[0]){
//                    resultTable[i][j]=0;
//                }
//                if(i==1&j>=P[0]){
//                    resultTable[i][j]=G[0];
//                }
                if(j<P[i-1]){
                    resultTable[i][j]=resultTable[i-1][j];
                }else{
                    //当前工人足够开采
                    //F(n,w)=Max(F(n-1,w),F(n-1,w-P[n-1])+G(n-1))，n>=1且w>p[n-1]（金矿还有，且人手够）
                    resultTable[i][j] = Math.max(resultTable[i-1][j],resultTable[i-1][j-P[i-1]]+G[i-1]);
                }

            }
        }
        //最后一行最后一列就是最优的解
        //return resultTable[G.length][w];
        return resultTable;
    }

注意，这里没有写第一行时的边界条件赋值代码
原因：这个二维数组真正有意义的是从resultTable[1][1]开始的，在resultTable[0][:]或者resultTable[:][0]都是0，且没有实际意义的数据，代码最后选择性的取他们填充到第一行，完成初始第一行的赋值，
只要二维数组（表格）第一行数据有了，后面的数据都是可以完成求值

测试函数：

public static void main(String[] args) {
        int w = 10;
        int[] p ={5,5,3,4,3};
        int[] g = {400,500,200,300,350};
        int [][]resultTable;
        //System.out.println(getBestGoldMining(w,p,g));
        resultTable = getBestGoldMining(w,p,g);
                //打印表
        for (int i=0;i<resultTable.length;i++){
            for (int j =0;j<resultTable[i].length;j++){
                System.out.print(resultTable[i][j]+"   ");
            }
            System.out.println();
        }
    }

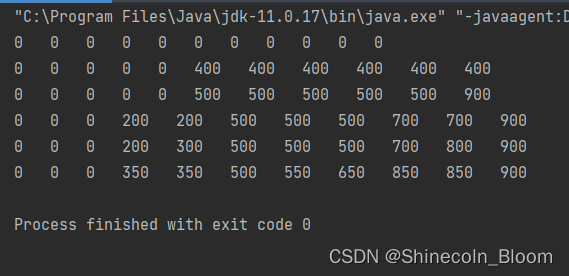
在这里插入图片描述

时间复杂度：O(nw)，嵌套for循环
空间复杂度：O(nw)，嵌套for循环

空间复杂度可以继续优化。

在表格中除第1行之外，每一行的结果都是由上一行数据推导出来的。

4个金矿、9个工人的最优结果，是由它的两个最优子结构，也就是3个金矿、5个工人和3个金矿、9个工人的结果推导而来的。这两个最优子结构都位于它的上一行。

C++实现如下：

#include <iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 100;
int w[N], v[N];
int f[N][N];
int n, m;
vector<int> cadidate;

void Transver(){
     for(int i = 1; i <= n; i ++){
         for(int j = 1; j <= m; j ++){
            printf("%d ", f[i][j]);
        }
        cout << endl;
     }
}

bool findIn(int x){
    bool flag = false;
    for(int i = 0; i < cadidate.size(); i ++){
        if (x == cadidate[i]){
             flag = true;
            break;
        }
    }
    return flag;
}

int findMin(int arr[], int n)
{
    int min = arr[1];
    cout << min << endl;
    for (int i = 2; i <= n; i++){
        if (arr[i] < min){
            min = arr[i];
        }
    }
    return min;
}

int main(){

    w[1] = 200;
    v[1] = 3;

    w[2] = 300;
    v[2] = 4;

    w[3] = 350;
    v[3] = 3;

    w[4] = 400;
    v[4] = 5;

    w[5] = 500;
    v[5] = 5;
    n = 5;
    m = 10;
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            if(j < v[i]) {
                f[i][j] = f[i-1][j]; 
            }
            else{
                if(f[i-1][j] >= f[i - 1][j - v[i]] + w[i]){
                    f[i][j] = f[i - 1][j];
                }else{
                    f[i][j] = f[i - 1][j - v[i]] + w[i];
                }
            }
        }
    }


    int x = n; int y = m;
    bool fg = true;
    // int a = findMin(v, 10);
    // printf("%d\n",a);
    

    while(y >= 3 || x >= 1){
        if(f[x][y] > f[x-1][y]){
            cadidate.push_back(x);
            y = y - v[x];
            x = x - 1;
            continue;
        }else if(f[x][y] == f[x-1][y]){
            x = x - 1;
            continue;
        }
        cadidate.push_back(x);
    }

    for(int i = 0; i < cadidate.size(); i ++){
        cout << cadidate[i] << endl;
    }
}

在这里插入图片描述

解法3，优化空间复杂度

解决方案
在程序中并不需要保存整个表格，无论金矿有多少座，我们只保存1行的数据即可。

    /**
     * 获得金矿最优收益
     * @param w  工人数量
     * @param G  金矿开采所需的工人数量
     * @param P  金矿储量
     * @return
     */
    public static int getMostGold(int w,int[]G,int[]P){
        int[] result = new int[w+1];
        //外层循环是不同金矿（不同行）
        //内层循环是不同工人数目（不同列）
        for (int i=1;i<=G.length;i++){
            for (int j=w;j>=1;j--){
                //人手够
                //result[j]是不挖当前的金矿(result[j]保留的就是上一行的数据,这里很妙。。)
                //result[j-P[i-1]]+G[i-1]是挖当前金矿
                if(j>=P[i-1]){
                    result[j]=Math.max(result[j],result[j-P[i-1]]+G[i-1]);
                }
            }
        }
        return result[w];
    }

这里一个很好的处理方式是result[j]=Math.max(result[j],result[j-P[i-1]]+G[i-1]);
其中result[j]表示当前金矿不挖（result[j]本来就保存的上一行的数据，就是不挖当前金矿）
其中result[j-P[i-1]]+G[i-1]表示挖当前金矿
这里重点是内层循环为for (int j=w;j>=1;j–)

测试方法：

public static void main(String[] args) {
        int w = 10;
        int[] p ={5,5,3,4,3};
        int[] g = {400,500,200,300,350};
        System.out.println(getMostGold(w,g,p));
    }

在这里插入图片描述

BUG

如果内层循环是从小到大
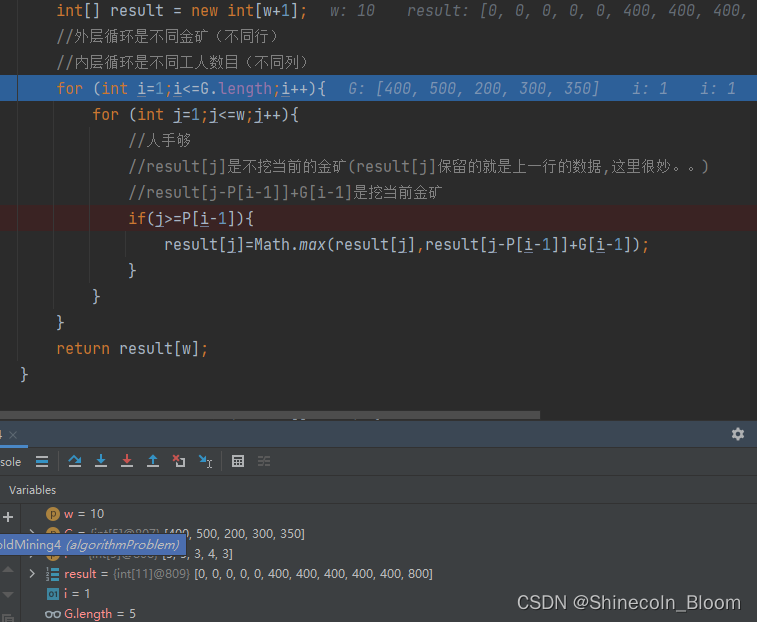
在这里插入图片描述
最后一个数组按理说是400，这里他取了result[5]+G[0]=400+400=800,出现了问题
原因是：result[5]的数据不在是第n-1行的值0，而是刚刚被更新过,成了400。
如果是从大到小遍历，前面没赋值的result[:]都是0，所以result[5]+G[0]=0+400=400…
本质原因是：新数据替换旧数据。

就是说，第n行数据是只依赖第n-1行数据。

如果从左到右的更新，到最右边的单元格所用的值可能被第n行数据覆盖掉了，导致错误
如果从右到左，可以保证在求第n行数据的每一个单元格，所用的数据都是来自n-1行的（不会被第n行数据覆盖。。）

时间复杂度：O(nw)
空间复杂度：O(n)
优化了空间复杂度

任然存在的问题

当工人很多的时候：n=5,w=1000（5座金矿，1000人来挖）
计算5000次，开辟1000个空间

如果使用递归
时间复杂度O(2ⁿ)=2⁵ =32次
空间复杂度O(n)=5

递归算法的空间复杂度：调用栈深度*每次递归的空间复杂度
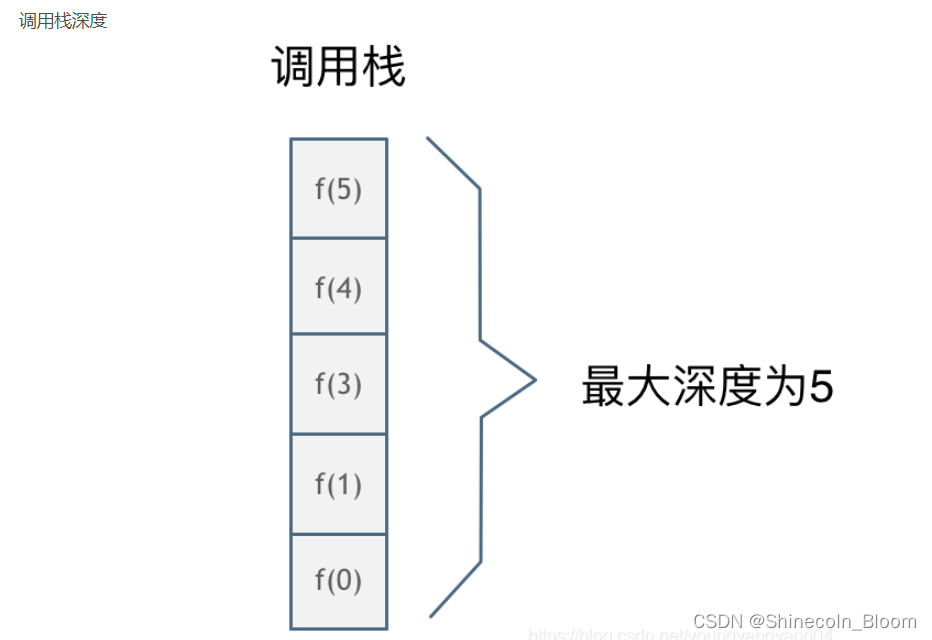
在这里插入图片描述

可以看出，当工人很多的时候，动态规划性能不如递归。

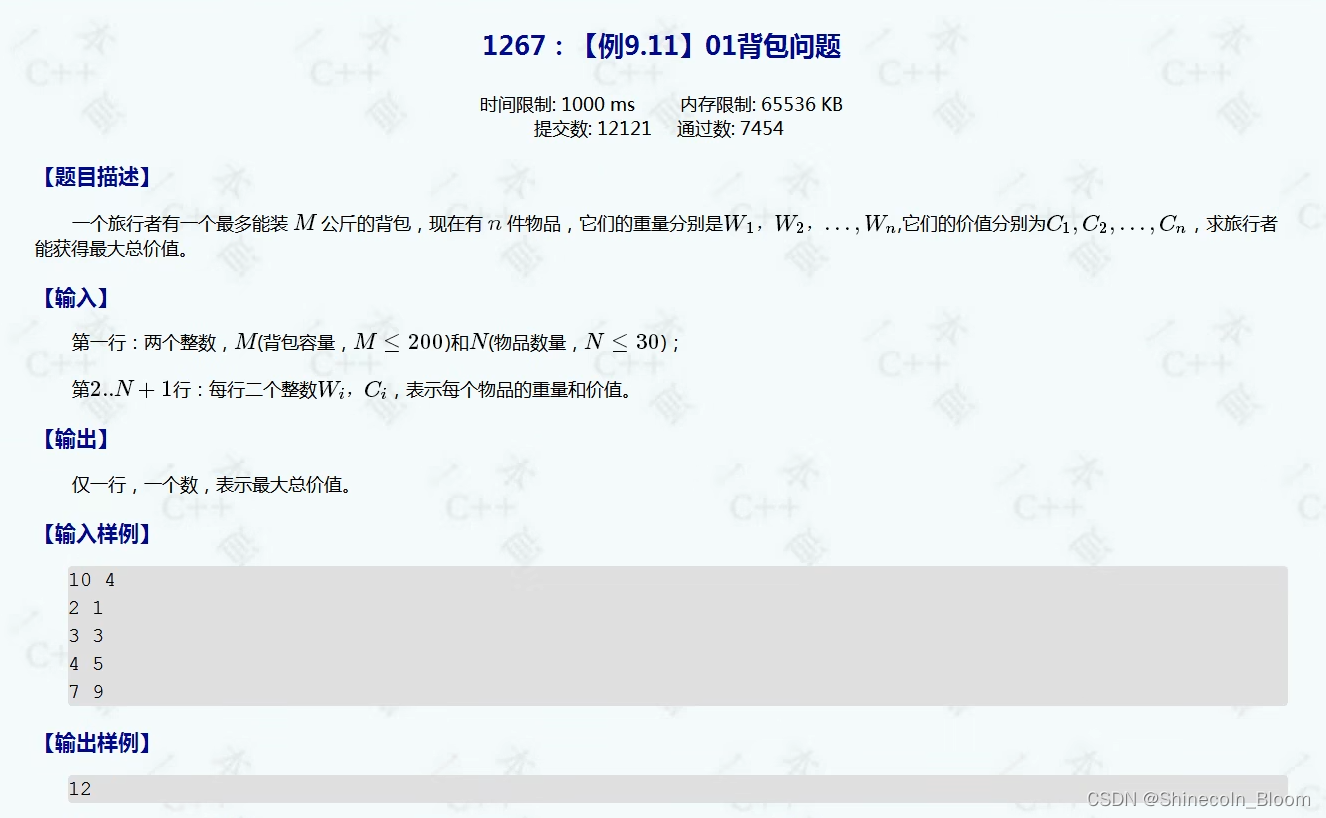
背包问题

01背包问题

01背包问题：每件物品只有1个所以最多只能用1次

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 i 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

面对每个物品，我们只有选择拿取或者不拿两种选择，不能选择装入某物品的一部分，也不能装入同一物品多次

0不拿
1拿

dp数组：dp[i][j]，其中 i 表示不同的物品，j 表示背包的剩余容量
dp数组的每一个值都是在物品为i，背包容量为j的最优解。
（一般都是从第一行开始逐层向后求，dp数组最后一行的最后一列就是问题的解）

可以通过dp数组推导状态转移方程式.
或者还是用这种思维：大问题分解为子问题；最优解=max(最后一个物体不拿的最优子结构，最后一个物体拿的最优子结构+最后一个物体的价值)

例如：
重量：W[]={2，3，4，7}
价值：C[]={1，3，5，9}
物品数目=4
背包容量=10

物品\背包容量	2	3	4	5	6	7	8	9	10
C[0]=0	0	0	0	0	0	0	0	0	0
C[1]=2	1	1	1	1	1	1	1	1	1
C[2] =3	1	3	3	3+1	3+1	3+1	3+1	3+1	3+1
C[3] =4	1	3	5	5	5+1	5+3	5+3	5+4	5+4
C[4] =7	1	3	5	5	6	9	9	9+1	9+3

这里构建表有三个要点：

从数组下标1开始，数组下标为0的都用0填充
从左上角开始，逐行向右推导到右下角，即：我们的最终结果
（m行n列格子里面的值表示：在前m个物品的条件下，背包容量为n的最优解）
对于每一个单元格的分析，采用大问题分解为子问题思想

F(n,w)=F(n-1,w)，n>=1且w<p[n-1]
（还有背包容量，但是所剩背包容量不够存放当前物品，就查看上一个物品，存放他们的最优解）
F(n,w)=0，n=0或w=0（当物品数目为0或者没有背包容量了，则不能再产生收益了，达到问题边界）
F(n,w)=Max(F(n-1,w),F(n-1,w-P[n-1])+G(n-1))，n>=1且w>p[n-1]（物品还有，且背包容量足够）
其中n是前n个物品，w是背包容量

在这里插入图片描述

对于一个单元格的具体分析如下：
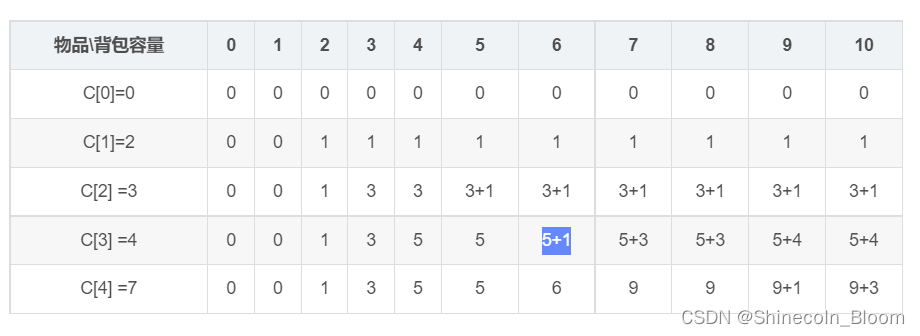
在这里插入图片描述

对于拿前三个物品且背包容量为6的情况分析如下：

不拿第三个物品：问题简化为在前2物品且背包容量为6的情况的最优解，就是表格的

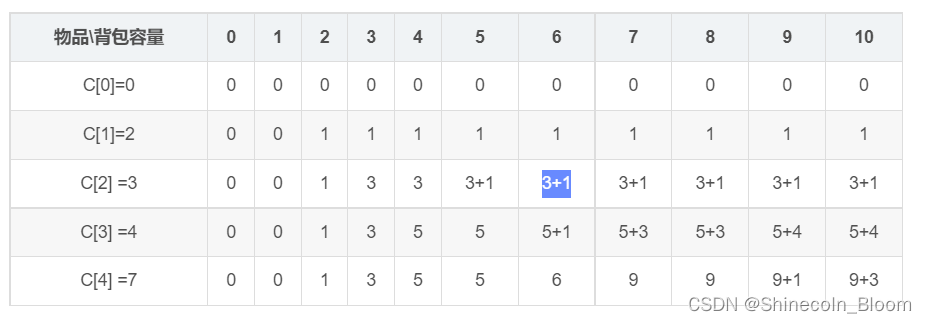
在这里插入图片描述

拿第三个物品：问题简化为在前2个物品且背包容量为2的情况的最优解 + 5

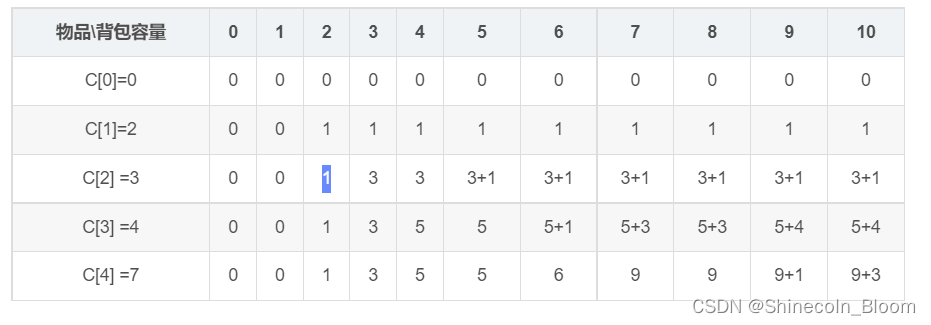
在这里插入图片描述
比较1和2的最大值，取5+1=6

在这里插入图片描述

问题建模

最优子结构

前3个物品，背包容量为10的最佳选择（第四个物品不拿）
前3个物品，背包容量为3的最佳选择（第四个物品拿）

究竟哪一种最优子结构可以通向全局最优解?
那就要看10个背包容量在前3个物品的收益，和3个背包容量在前3个物品收益+最后一个物品收益谁大谁小了。

状态转移方程式

在这里插入图片描述

边界

F(n,w)=0，n=0或w=0（当物品数目为0或者没有背包容量了，则不能再产生收益了，达到问题边界）

求解问题

动态规划（2维DP表）JAVA

/**
     * 0-1背包问题（dp二维数组实现）
     * @param n  背包容量
     * @param W  重量数组
     * @param C  价值数组
     * @return
     */
    public static int[][] getMostValue(int n,int[]W,int[]C){
        int[][]dp = new int[W.length+1][n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=W.length;i++){
            for (int j=1;j<=n;j++){
                //当前背包容量装不下了,就是排除当前商品，前面所有商品的最优解
                if(j<W[i-1]){
                    dp[i][j] = dp[i-1][j];
                }else {
                    //背包装的下的情况
                    //dp[i-1][j]不拿当前商品
                    //dp[i-1][j-W[i]]+C[i]拿当前商品(注意这里是 W[i]和C[i])
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-W[i-1]]+C[i-1]);

                }
            }
        }
        return dp;
    }

测试方法：

public static void main(String[] args) {
        int []W = new int[]{2,3,4,7};
        int []C = new int[]{1,3,5,9};
        int n =10;//背包容量
        int[][]dp;
        dp = getMostValue(n,W,C);

        //打印二维数组
        for (int i=0;i<dp.length;i++){
            for (int j =0;j<dp[i].length;j++){
                System.out.print(dp[i][j]+"   ");
            }
            System.out.println();
        }
    }

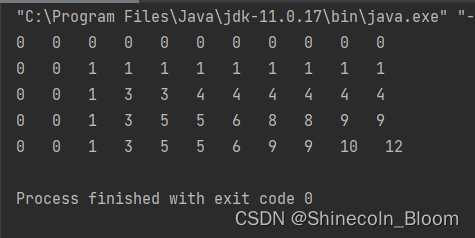
在这里插入图片描述
同表：

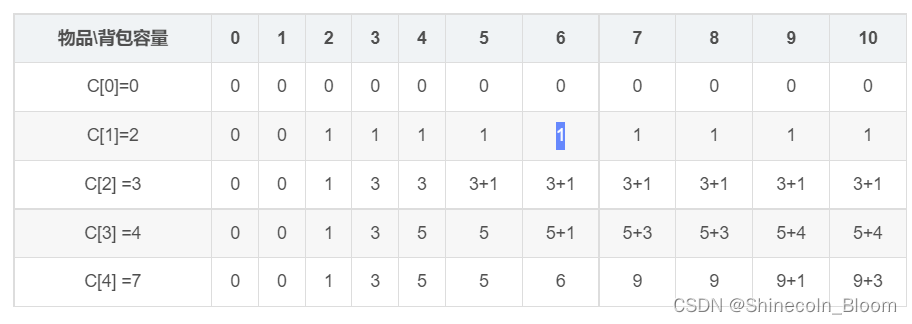
动态规划后无效性原则：当前状态只和上一个状态有关
在dp数组（表）中表现为，只和上一行有关。
利用滚动数组优化空间复杂度。。。（压缩数组）

压缩数组（1维DP表）

通过不断刷新一维数组的值，优化空间复杂度。
动态规划后无效性原则：当前状态只和上一个状态有关

压缩数组，就是压缩的行维度–>把 i 去掉
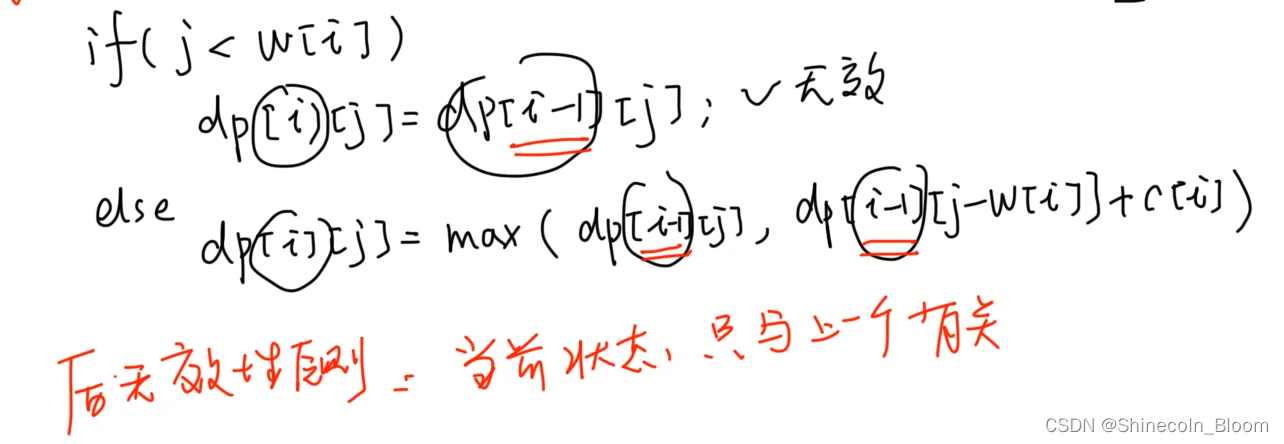
在这里插入图片描述

压缩数组的状态转移方程式

因此，压缩数组后的状态转移方程式为：
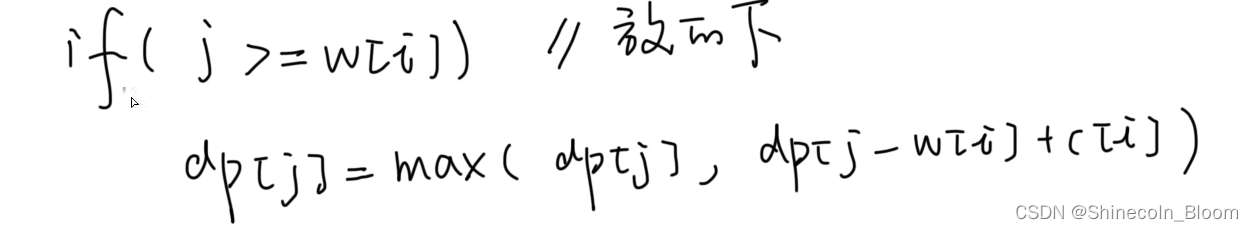
在这里插入图片描述

从右到左写循环（防止n-1层的值被自己覆盖）

JAVA求解

/**
     * 0-1背包问题（dp二维数组实现）
     * @param n  背包容量
     * @param W  重量数组
     * @param C  价值数组
     * @return
     */
    public static int[] getMostValue(int n,int[]W,int[]C){
        int[]dp = new int[n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=W.length;i++) {
            for (int j = n; j >= 1; j--) {
                //当前背包容量装不下了,就是排除当前商品，前面所有商品的最优解
                //这里用了压缩数组，之前物品的最优解就是不更新数组的值。。。
                //所以数组值不动，这个代码可以去掉了。。
//            if(j<W[i-1]){
//                dp[j] = dp[j];
//            }else {
                if(j>=W[i-1]) {
                    //背包装的下的情况
                    //dp[j]不拿当前商品
                    //dp[j-W[i]]+C[i]拿当前商品(注意这里是 W[i]和C[i])
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }
            //每一行打印一下dp数组
            for (int k=0;k<=n;k++){
                System.out.print(dp[k]+"  ");
            }
            System.out.println();
        }

        return dp;
    }

测试函数：

public static void main(String[] args) {
        int []W = new int[]{2,3,4,7};
        int []C = new int[]{1,3,5,9};
        int n =10;//背包容量
        int[]dp;
        dp = getMostValue(n,W,C);

        System.out.println("打印最后的dp数组: ");
        //打印二维数组
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
            }
            System.out.println();

    }

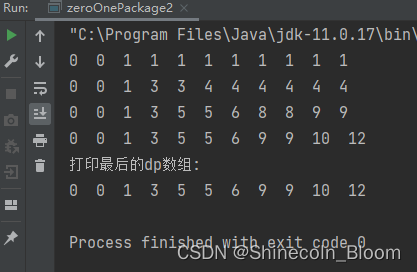
在这里插入图片描述

在次看看如果从前往后推导结果如何：

for (int j = 1; j <= n; j++) {......}

在这里插入图片描述
这是错误的结果。。。
参考资料

01背包总结

0/1背包问题是最基本的背包问题，它包含了背包问题中设计状态、方程的最基本思想；
另外，别的类型的背包问题往往也可以转换成0/1背包问题求解。

完全背包问题

在这里插入图片描述

和01背包的区别：

完全背包问题：每种物品的数量无限。
01背包问题：每种物品数目只有1个，只能选或者不选

物品数目的取值范围：[0，当前背包容量/物品重量]
对于在前 i 个物品中,背包容量为 j 的情况下（i 行 j 列单元格）:第 i 个物品数目的取值范围 [0，j/W[i] ]

因此，对01背包代码修改max()函数内容（修改状态转移方程式）就行；
01背包状态转移方程式max()里面就是Max(不拿,拿）这俩种情况
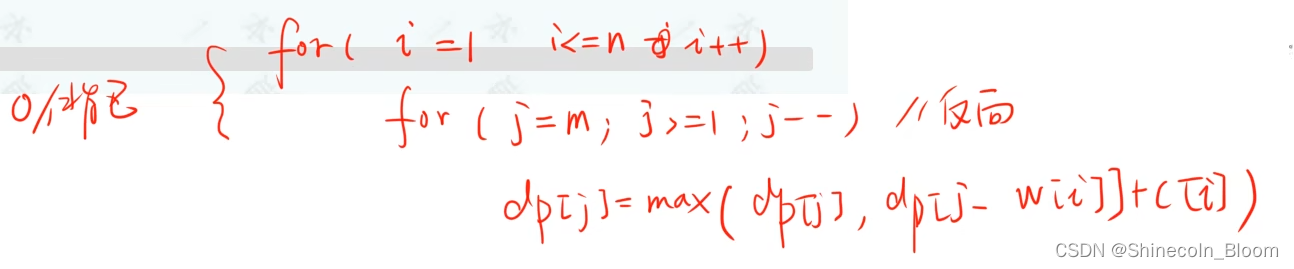
在这里插入图片描述
修改成完全背包:

当k=1时，代码退化为01背包了
这个代码就是对01背包的扩展：本来俩层循环就完成了一行dp数组的写入更新，现在又多了最内的一层循环，就是对dp数组每个写入位置j在进行循环判断，在拿不同当前数目的物品时，从中选择最佳的。。。

问题建模

最优子结构

状态转移方程式

0-1背包的dp数组表
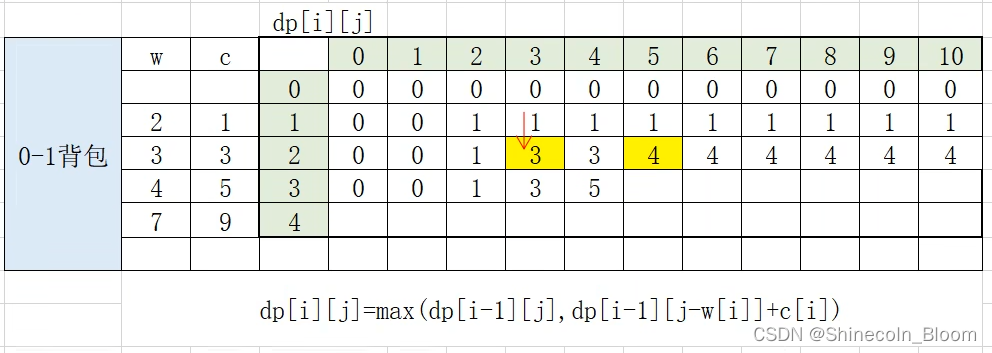
在这里插入图片描述
对应的JAVA核心代码：

for (int j = n; j >= 1; j--) {
        if(j>=W[i-1]) {
             dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
         }
}

逆向for循环推，用的是i-1行数据(上一行的旧数据)

完全背包的dp数组表：
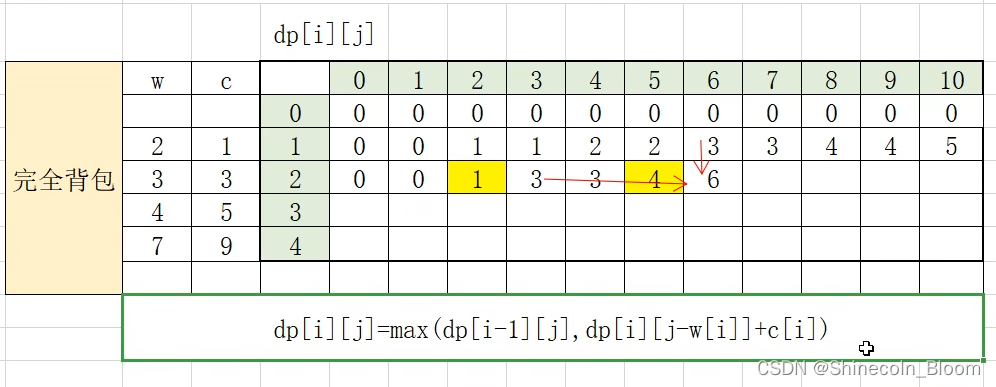
在这里插入图片描述

得到了完全背包的状态转移方程式。

因为完全背包可以拿多次重复的元素，所以最优子结构更新为本行左边的值

观察DP表可知：上一行的最优解>=上上行，甚至所有之前行的最优解

对应的JAVA核心代码：

 //从前往后推（因为状态转移公式用到了本行数据）
            for (int j = 1; j <=n ; j++) {
                if(j>=W[i-1]) {
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }

正向for循环推，用的就是 i 行数据 (本行的新数据)
正向推理的话，可以用到本行的刚得出的新数据。。。

边界

求解问题

朴素的解法

用for循环完成：Max(不取当前商品，取一个当前商品，取俩个当前商品，…取j/W[i-1]个当前商品)

/**
     * 对0-1背包问题的扩展（dp一维数组实现）
     * @param n  背包容量
     * @param W  重量数组
     * @param C  价值数组
     * @return
     */
    public static int[] getMostValue(int n,int[]W,int[]C){
        int[]dp = new int[n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=W.length;i++) {
            for (int j = n; j >= 1; j--) {
                //当前背包容量装不下了,就是排除当前商品，前面所有商品的最优解
                //这里用了压缩数组，之前物品的最优解就是不更新数组的值。。。
                //所以数组值不动，这个代码可以去掉了。。
//            if(j<W[i-1]){
//                dp[j] = dp[j];
//            }else {
                if(j>=W[i-1]) {
                    //背包装的下的情况
                    //dp[j]不拿当前商品
                    //dp[j-k*W[i]]+k*C[i]拿当前商品(拿k个)
                    //对一次拿几个物品进行循环，最少什么都不拿，最大拿j/W[i-1]个
                    //k=1就是01背包...
                    //就是说：对于dp数组的每一个j点，在进行循环（拿多少个当前商品的循环,选择最好的情况）
                    //Max(不拿当前商品，拿一个当前商品，拿2个当前商品，...拿j/W[i-1]个当前商品)
                    for (int k=1;k<=j/W[i-1];k++) {
                        dp[j] = Math.max(dp[j], dp[j - k*W[i-1]] + k*C[i-1]);
                    }
                }
            }
            //每一行打印一下dp数组
            for (int k2=0;k2<=n;k2++){
                System.out.print(dp[k2]+"  ");
            }
            System.out.println();
        }

        return dp;
    }

和01背包代码区别即：

for (int k=1;k<=j/W[i-1];k++) {
                        dp[j] = Math.max(dp[j], dp[j - k*W[i-1]] + k*C[i-1]);
                    }

上面代码等价于如下代码：

dp[j] = Math.max(dp[j], dp[j - 1*W[i-1]] + 1*C[i-1],dp[j - 2*W[i-1]] + 2*C[i-1],.........dp[j - (j/W[i-1])*W[i-1]] + (j/W[i-1])*C[i-1]);

测试方法：

public static void main(String[] args) {
        int []W = new int[]{2,3,4,7};
        int []C = new int[]{1,3,5,9};
        int n =10;//背包容量
        int[]dp;
        dp = getMostValue(n,W,C);

        System.out.println("打印最后的dp数组: ");
        //打印二维数组
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
        }
        System.out.println();

    }

在这里插入图片描述

新递推公式的解法

dp[i][j]=max(dp[i-1][j]，dp[i][j-w[i-1]]+C[i-1])
用的是：本行该单元格位置前面的数据

/**
     * 对0-1背包问题的扩展（dp一维数组实现）
     * dp[i][j]=max(dp[i-1][j]，dp[i][j-w[i-1]]+C[i-1])
     * 用了本行的数据（需要从左往右推）
     * @param n  背包容量
     * @param W  重量数组
     * @param C  价值数组
     * @return
     */
    public static int[] getMostValue(int n,int[]W,int[]C){
        int[]dp = new int[n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=W.length;i++) {
            //从前往后推（因为状态转移公式用到了本行数据）
            for (int j = 1; j <=n ; j++) {
                if(j>=W[i-1]) {
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }
            //每一行打印一下dp数组
            for (int k2=0;k2<=n;k2++){
                System.out.print(dp[k2]+"  ");
            }
            System.out.println();
        }

        return dp;
    }

用到本行数据：正向for循环

测试方法：

public static void main(String[] args) {
        int []W = new int[]{2,3,4,7};
        int []C = new int[]{1,3,5,9};
        int n =10;//背包容量
        int[]dp;
        dp = getMostValue(n,W,C);

        System.out.println("打印最后的dp数组: ");
        //打印二维数组
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
        }
        System.out.println();

    }

在这里插入图片描述

完全背包和01背包区别&完全背包总结

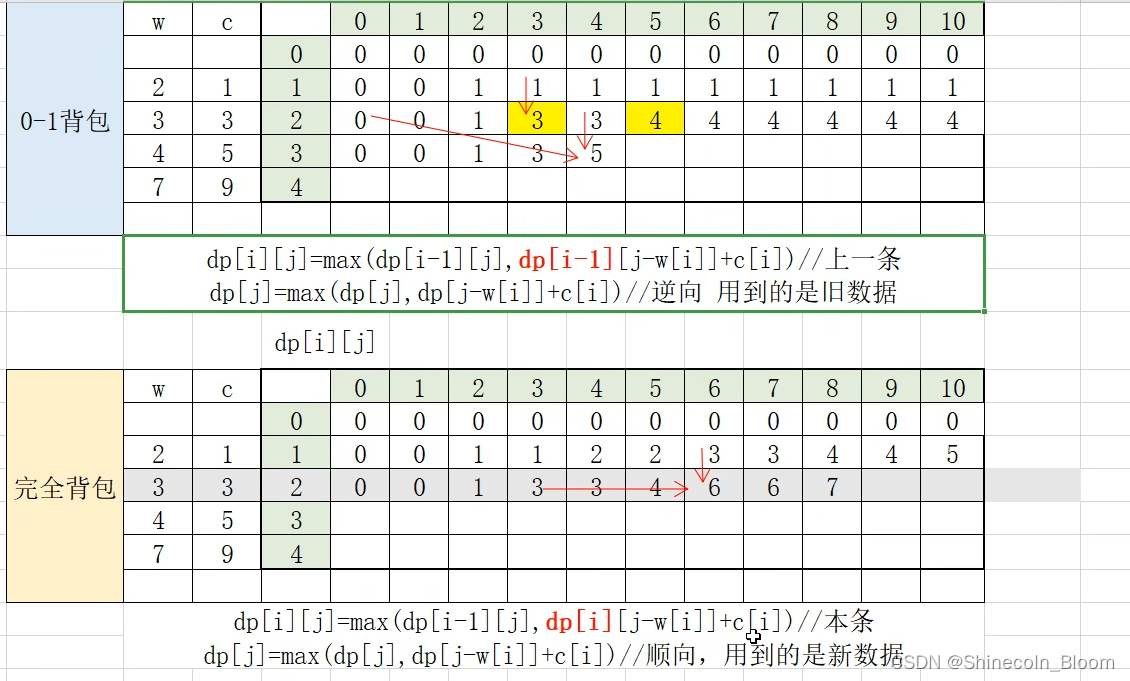
在这里插入图片描述

状态转移公式的不同
红色就是他们递推公式不同的地方：
01背包的状态转移公式用的是上一条数据
完全背包的状态转移公式用的是本条数据
在压缩数组的代码中的不同
在压缩数组的代码里面体现的就是for循环顺序不一样

01背包：

        for (int i=1;i<=W.length;i++) {
        //从后往前推（因为状态转移公式用到了上一行数据）
            for (int j = n; j >= 1; j--) {
                if(j>=W[i-1]) {
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }
        }

完全背包：

        for (int i=1;i<=W.length;i++) {
            //从前往后推（因为状态转移公式用到了本行数据）
            for (int j = 1; j <=n ; j++) {
                if(j>=W[i-1]) {
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }
        }

参考资料

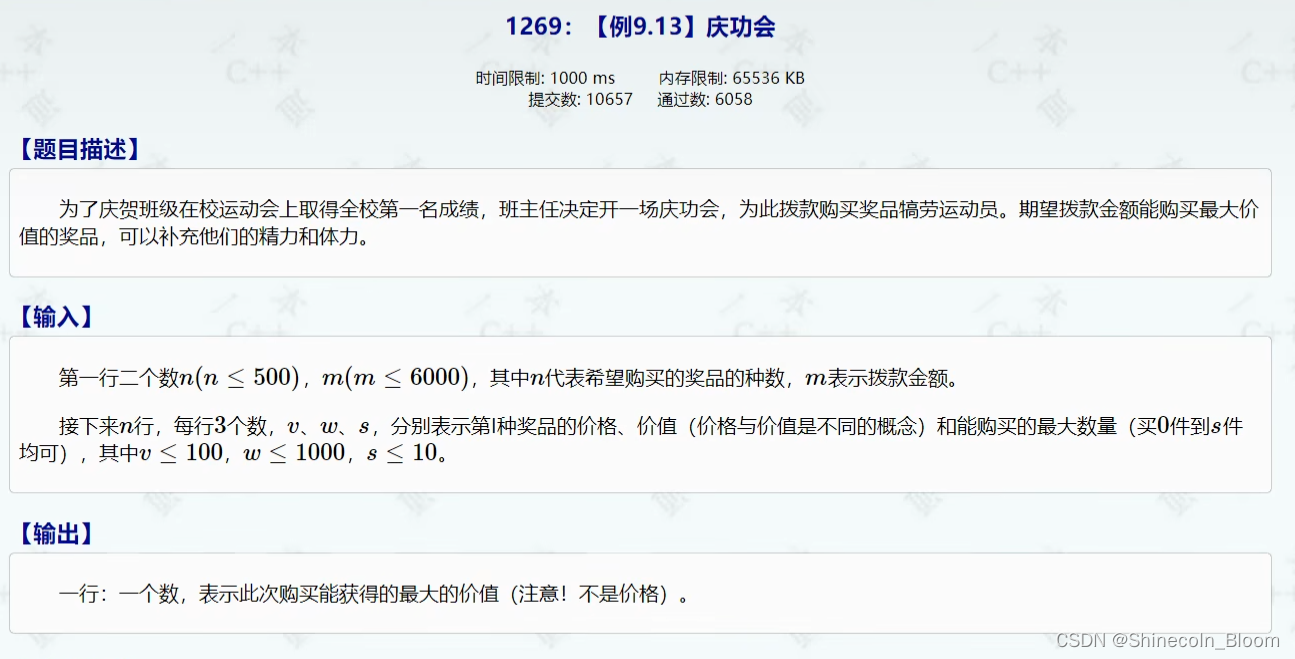
多重背包问题

有N种物品和一个容量为V的背包。第 i 种物品最多有 n[ ] 件可用，每件费用是 c[ i ]，价值是w [ i ]。
求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

问题分析:我们仔细观察题目，会发现不同点在于每种物品的数量，
01背包是每种只有1件，
完全背包是每种无限件，
多重背包是每种有限件。

在这里插入图片描述

问题建模

最优子结构

状态转移方程

边界

求解问题

朴素解法

由01背包的代码修改而来
加上俩个限制条件：（需同时满足如下限制条件）

物品个个数小于等于当前物品题目限制的可用最大数目
物品个数小于等于（当前背包容量/当前物品重量）

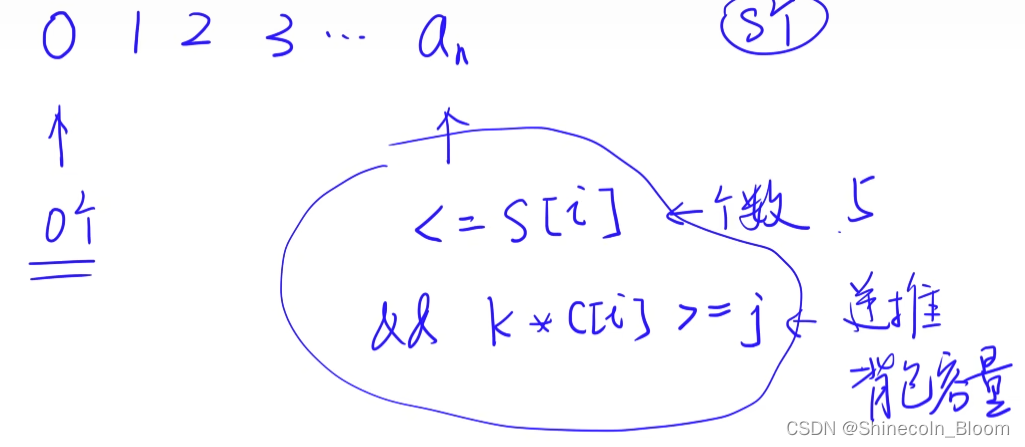
在这里插入图片描述

设：myMin = Math.min(S[i-1]，j/V[i-1])
其中S[i-1]是题目限制的i个物品所能使用最大值

和01背包代码区别即：

for (int k =1;k<=Math.min(S[i-1],j/V[i-1]);k++){
                        dp[j] = Math.max(dp[j], dp[j - k*V[i-1]] + k*W[i-1]);
                    }

上面代码等加入如下代码：

dp[j] = Math.max(dp[j], dp[j - 1*W[i-1]] + 1*C[i-1],dp[j - 2*W[i-1]] + 2*C[i-1],.........dp[j - myMin*W[i-1]] + myMin*C[i-1]);

JAVA实现如下：

/**
     * 0-1背包问题x修改而来（dp一维数组实现）
     * 添加物品数目的限制条件（for循环实现）
     * @param n   总金钱(相当于之前的背包容量)
     * @param V   价格 (相当于之前的物品重量)
     * @param W   价值(最大化价值)
     * @param S   当前物品能购买最大数目
     * @return
     */
    public static int[] getMostValue(int n,int[]V,int[]W,int[]S){
        int[]dp = new int[n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=V.length;i++) {
            for (int j = n; j >= 1; j--) {
                //当前背包容量装不下了,就是排除当前商品，前面所有商品的最优解
                //这里用了压缩数组，之前物品的最优解就是不更新数组的值。。。
                //所以数组值不动，这个代码可以去掉了。。
                if(j>=V[i-1]) {
                    //背包装的下的情况
                    //dp[j]不拿当前商品
                    //dp[j-V[i-1]] + W[i-1]拿当前商品 (注意这里不是 W[i]和C[i])
                    for (int k =1;k<=Math.min(S[i-1],j/V[i-1]);k++){
                        dp[j] = Math.max(dp[j], dp[j - k*V[i-1]] + k*W[i-1]);
                    }

                }
            }
            //每一行打印一下dp数组
            for (int k=0;k<=n;k++){
                System.out.print(dp[k]+"  ");
            }
            System.out.println();
        }

        return dp;
    }

测试方法如下：

    public static void main(String[] args) {
//        int []W = new int[]{2,3,4,7};
//        int []C = new int[]{1,3,5,9};
        int []V = new int[]{80,40,30,40,20}; //价格 (相当于01背包物体的重量)
        int []W = new int[]{20,50,50,30,20}; //价值 (目的是使得价值最大化)
        int []S = new int[]{4,9,7,6,1}; //能购买最大数量

        int n =1000;//背包容量
        int[]dp;
        dp = getMostValue(n,V,W,S);

        System.out.println("打印最后的dp数组: ");
        //打印二维数组
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
        }
        System.out.println();
    }

运行的结果如下：

"C:\Program Files\Java\jdk-11.0.17\bin\java.exe" "-javaagent:D:\Program Files\JetBrains\IntelliJ IDEA Community Edition 2021.2.2\lib\idea_rt.jar=6824:D:\Program Files\JetBrains\IntelliJ IDEA Community Edition 2021.2.2\bin" -Dfile.encoding=UTF-8 -classpath E:\Code\softwareEngineer\out\production\softwareEngineer algorithmProblem.multipleBackpack
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  20  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  40  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  60  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  80  
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  490  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  510  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  530  
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  840  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  20  20  20  20  20  20  20  20  20  20  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  70  70  70  70  70  70  70  70  70  70  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  120  120  120  120  120  120  120  120  120  120  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  170  170  170  170  170  170  170  170  170  170  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  220  220  220  220  220  220  220  220  220  220  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  270  270  270  270  270  270  270  270  270  270  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  320  320  320  320  320  320  320  320  320  320  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1040  1040  1040  1040  1040  1040  1040  1040  1040  1040  1040  
打印最后的dp数组: 
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  20  20  20  20  20  20  20  20  20  20  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  50  70  70  70  70  70  70  70  70  70  70  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  100  120  120  120  120  120  120  120  120  120  120  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  150  170  170  170  170  170  170  170  170  170  170  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  200  220  220  220  220  220  220  220  220  220  220  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  250  270  270  270  270  270  270  270  270  270  270  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  300  320  320  320  320  320  320  320  320  320  320  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  350  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  370  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  400  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  420  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  450  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  470  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  500  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  520  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  550  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  570  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  600  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  620  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  650  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  670  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  700  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  720  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  750  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  770  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  800  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  820  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  830  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  850  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  860  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  880  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  890  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  910  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  920  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  940  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  950  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  970  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  980  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1000  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1020  1040  1040  1040  1040  1040  1040  1040  1040  1040  1040  1040

样例的输出结果为：
在这里插入图片描述

存在的问题：在判断取多少个当前物品时，使用了for循环，增加了时间复杂度。
优化内层的for循环去掉他，减少时间复杂度

多重背包的二进制优化

二进制优化算法

在这里插入图片描述

任意的一个正整数n，都可以被分解成1,2,4,…,2^(k-1),2^k，S-2^k+1+1的形式。（最后一个差分可能不是2的整数幂次）
任意的n都可以由上述二进制数目组合而成

在这里插入图片描述

多重背包的二进制拆分

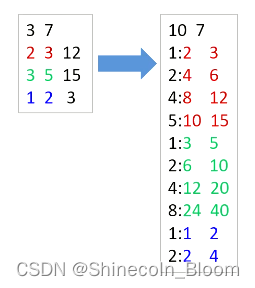
在这里插入图片描述

把30件物品（3种不同的物品）转换为10件物品（10种不同的物品）进行01背包求解
因为这样拆分后，每种不同的物品只有1个了，只有选和不选。。。。。（01背包）
可以这样拆分的原因就是：任意的一个正整数n，都可以被分解成1,2,4,…,2(k-1),2k，S-2k+1+1的形式。
原本限制条件是：总钱数不能超过和每种物品选择的次数不超过限制
拆分可以看成后限制条件：只有总钱数限制（退化为01背包）
原因是二进制拆分可以表示任意的数字

在这里插入图片描述

二进制拆分JAVA代码

//二进制拆分
    public static Map<String,int[]> binaryResolution(int[]V,int[]W,int[]S,int[]VV,int[]WW){
        //拆分后，物品的数目的计数
        int num = 1;
        //外层对不拆分之前的不同物品循环
        for (int i = 1;i<=V.length;i++){
            //基于当前物品能购买最大数量，进行二进制拆分操作。
            for (int j=1;j<S[i-1];j=j<<1){
                VV[num] = j*V[i-1];
                WW[num++]=j*W[i-1];
                S[i-1]=S[i-1]-j;//二进制拆分
            }
            //执行到这一步，S[i-1]的值为：S-2(k+1)次幂+1(
            // 最后一个差分可能不是2的整数幂次）
            if(S[i-1]!=0){
                VV[num]=S[i-1]*V[i-1];
                WW[num++] = S[i-1]*W[i-1];
            }
        }
        Map<String, int[] > map = new HashMap<String, int[]>();
        map.put("WW",WW);
        map.put("VV",VV);
        return map;
    }

在用压缩数组的01背包处理二进制拆分后的新数据

/**
     * 0-1背包问题（dp一维数组实现）
     * @param n  背包容量
     * @param W  重量数组
     * @param C  价值数组
     * @return
     */
    public static int[] getMostValue(int n,int[]W,int[]C){
        System.out.println("打印dp二维数组（表）");
        int[]dp = new int[n+1];
        //外层循环是拿不同物品（不同行）
        //内层循环是不同背包容量(不同列)
        //下标为0的数组，值全是0
        for (int i=1;i<=W.length;i++) {
            for (int j = n; j >= 1; j--) {
                //当前背包容量装不下了,就是排除当前商品，前面所有商品的最优解
                //这里用了压缩数组，之前物品的最优解就是不更新数组的值。。。
                //所以数组值不动，这个代码可以去掉了。。
//            if(j<W[i-1]){
//                dp[j] = dp[j];
//            }else {
                if(j>=W[i-1]) {
                    //背包装的下的情况
                    //dp[j]不拿当前商品
                    //dp[j-W[i]]+C[i]拿当前商品(注意这里是 W[i]和C[i])
                    dp[j] = Math.max(dp[j], dp[j - W[i-1]] + C[i-1]);
                }
            }
            //每一行打印一下dp数组

            for (int k=0;k<=n;k++){
                System.out.print(dp[k]+"  ");
            }
            System.out.println();
        }
        return dp;
    }

测试函数:

public static void main(String[] args) {

        int []V = new int[]{2,3,1}; //价格 (相当于01背包物体的重量)
        int []W = new int[]{3,5,2}; //价值 (目的是使得价值最大化)
        int []S = new int[]{12,15,3}; //能购买最大数量

        int power=0;//在S数组中，计算大于每一个值的：2的最小次幂(也就是拆分后元素的个数)
        for (int e:S){
            for (int i =1;i<e;i=i<<1){
                power++;
            }
        }
        //二进制拆分后得到新的VV和WW
        int []VV = new int[power+1] ; //价格 (相当于01背包物体的重量)
        int []WW = new int[power+1]; //价值 (目的是使得价值最大化)
        int n =7;//背包容量
        int[]dp;//dp数组
        Map<String, int[] > map = new HashMap<String, int[]>();
        map = binaryResolution(V,W,S,VV,WW);
        VV=map.get("VV");
        WW = map.get("WW");
        //打印差分后的数组(下标为0不存数据)
        System.out.println("价格拆分后为： ");
        for (int i =1;i<VV.length;i++){
            System.out.print(VV[i]+"  ");
        }
        System.out.println();
        System.out.println("价值拆分后为： ");
        for (int i =1;i<WW.length;i++){
            System.out.print(WW[i]+"  ");
        }
        System.out.println();

        //调用01背包代码(对拆分后的进行求解)
        dp = getMostValue(n,VV,WW);

        System.out.println("打印最后的dp数组: ");
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
        }
        System.out.println();
    }

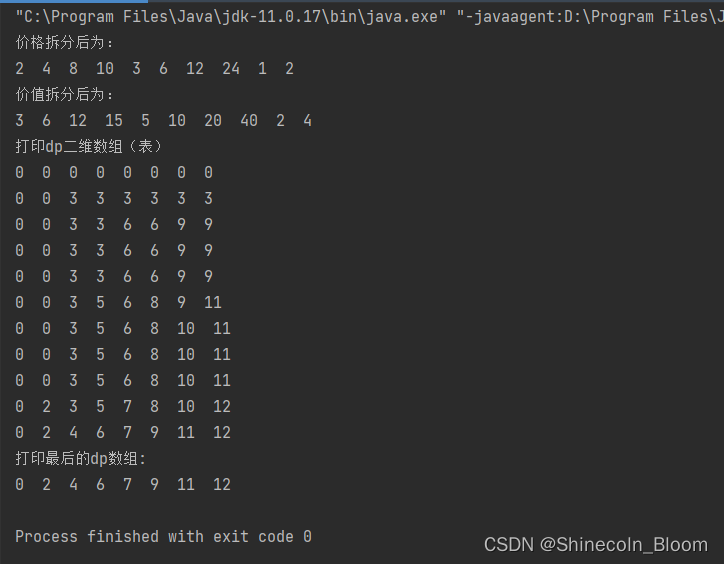
在这里插入图片描述
二进制拆分图：

参考资料

对于本章一开始那个题目的测试如下：

public static void main(String[] args) {

        int []V = new int[]{80,40,30,40,20}; //价格 (相当于01背包物体的重量)
        int []W = new int[]{20,50,50,30,20}; //价值 (目的是使得价值最大化)
        int []S = new int[]{4,9,7,6,1}; //能购买最大数量

        int power=0;//在S数组中，计算大于每一个值的：2的最小次幂(也就是拆分后元素的个数)
        for (int e:S){
            for (int i =1;i<=e;i=i<<1){
                power++;
            }
        }
        System.out.println("二进制拆分为： "+power+"个不同物品");
        //二进制拆分后得到新的VV和WW
        int []VV = new int[power+1] ; //价格 (相当于01背包物体的重量)
        int []WW = new int[power+1]; //价值 (目的是使得价值最大化)
        int n =1000;//背包容量
        int[]dp;//dp数组
        Map<String, int[] > map = new HashMap<String, int[]>();
        map = binaryResolution(V,W,S,VV,WW);
        VV=map.get("VV");
        WW = map.get("WW");
        //打印差分后的数组(下标为0不存数据)
        System.out.println("价格拆分后为： ");
        for (int i =1;i<VV.length;i++){
            System.out.print(VV[i]+"  ");
        }
        System.out.println();
        System.out.println("价值拆分后为： ");
        for (int i =1;i<WW.length;i++){
            System.out.print(WW[i]+"  ");
        }
        System.out.println();

        //调用01背包代码(对拆分后的进行求解)
        dp = getMostValue(n,VV,WW);

        System.out.println("打印最后的dp数组: ");
        for (int i=0;i<=n;i++){
            System.out.print(dp[i]+"  ");
        }
        System.out.println();
    }