本文内容借鉴一本我非常喜欢的书——《数据结构与算法图解》。学习之余,我决定把这本书精彩的部分摘录出来与大家分享。??
本章内容
写在前面
大 O记法能客观地衡量各种算法的时间复杂度,是比较算法的利器。我们也试过用它来对比二分查找和线性查找的步数差异,发现二分查找的步数为 O(log N),比线性查找的 O(N)快得多。
然而,写代码的时候并不总有这样明确的二选一,更多时候你可能就直接采用首先想到的那种算法了。不过有了大 O的话,你就可以与其他常用的算法比较,然后问自己:“我的算法跟它们相比,是快还是慢?”
如果你通过大 O 发现自己的算法比其他的要慢,你就应该退一步,好好想想怎样优化它,才能使它变成更快的那种大 O。
本章我们会写些代码来解决一个实际问题,并且会用大 O 来测量算法的性能,然后看看是否能对算法做些修改,使得性能提升。
1.冒泡排序
排序算法是计算机科学中被广泛研究的一个课题。历时多年,它发展出了数十种算法,这些算法都着眼于一个问题:
如何将一个无序的数字数组整理成升序?
冒泡排序是一种很基本的排序算法,步骤如下。
(1) 指向数组中两个相邻的元素(最开始是数组的头两个元素),比较它们的大小。
(2) 如果它们的顺序错了(即左边的值大于右边),就互换位置。?
如果顺序已经是正确的,那这一步就什么都不用做。
(3) 将两个指针右移一格。
重复第(1)步和第(2)步,直至指针到达数组末尾。?
(4)重复第(1)至(3)步,直至从头到尾都无须再做交换,这时数组就排好序了
这里被重复的第(1)至(3)步是一个轮回,也就是说,这个算法的主要步骤被“轮回”执行直到整个数组的顺序正确。
2.冒泡排序实战
下面来举一个完整的例子。假设要对 [4, 2, 7, 1, 3] 进行排序,产生一个升序的数组。
开始第 1次轮回。
数组一开始如下图所示。
第 1步:首先,比较 4和 2。如图可见它们的顺序是错的
第 2步:交换它们的位置。?
第 3步:比较 4和 7。
它们的顺序正确,所以不用做什么交换。?
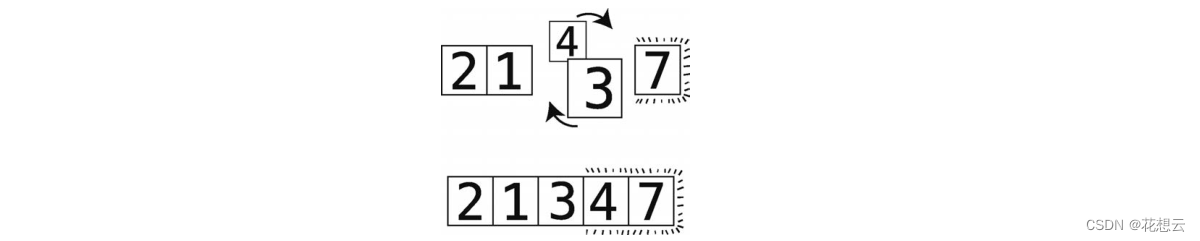
第 4步:比较 7和 1。
第 5步:顺序错误,于是进行交换。
第 6步:比较 7和 3。
第 7步:顺序错误,于是进行交换。
?
因为我们一直把较大的元素换到右边,所以现在最右侧的 7正处于其正确位置上。这也正是此种算法名为冒泡排序的原因:每一次轮回过后,未排序的值中最大的那个都会“冒”到正确的位置上。?
因为刚才那次轮回做了不止一次的交换,所以得继续轮回。
下面来第 2次轮回。
此时 7已经在正确的位置上了。
第 8步:从比较 2和 4开始。
它们已经按顺序排好了,所以直接进行下一步。
第 9步:比较 4和 1。
第 10步:它们的顺序错误,于是交换。
第 11步:比较 4和 3。
第 12步:顺序错误,进行交换。
因为 7 已经在上一次轮回里排好了,所以无须比较 4 和 7。此外,4 移到了正确的位置,本次轮
回结束。?因为这次轮回也做了不止一次的交换,所以得继续轮回。
下面来第 3次轮回。
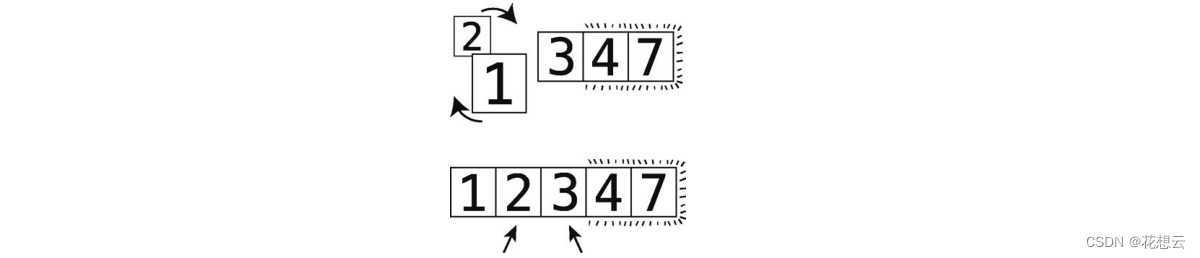
第 13步:比较 2和 1。
第 14步:顺序错误,进行交换。
第 15步:比较 2和 3。
顺序正确,不用交换。?
这时 3也“冒”到其正确位置了。因为这次轮回做了不止一次的交换,所以还要继续。
于是开始第 4次轮回。
第 16步:比较 1和 2。
顺序正确,不用交换。而且剩下的元素也都排好序了,轮回结束。
因为刚才的轮回没有任何交换,可知整个数组都已排好序。
?
3.冒泡排序的实现
以下是用 C语言写的冒泡排序。
void BubbleSort(int arr[], int n) //n为数组的大小
{
for (int i = 0; i < n-1; i++)//n个数字,把n-1个排好,剩下一个自然在正确的位置
{
for (int j = 0; j < n - 1 - i; j++)//每一个轮回之后,末端的数字已经到了正确的位置上,不需要比较
{
//比较相邻数字
//升序为 >,降序为 <
if (arr[j] > arr[j + 1])
{
//交换两个数字的位置
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}解释:
这里的实现用了两层循环。最外层的循环用i来控制,表示的是一个轮回。
i<n-1,其含义为有n个数,只需要走n-1个轮回。因为,我们把n-1个数排好之后,剩下的那个数自然在正确的位置上了。
内层循环由j来控制,进行的是一次轮回中,把一个数“冒”到正确的位置上。
此处的代码就是对上一小节冒泡排序实战的翻译。
4.冒泡排序的效率
冒泡排序的执行步骤可分为两种。
比较:比较两个数看哪个更大。
交换:交换两个数的位置以使它们按顺序排列。
先看看冒泡排序要进行多少次比较。
回顾之前那个 5个元素的数组,你会发现在第 1次轮回我们为 4对元素进行了 4次比较。
到了第 2次轮回,则只做了 3次比较。这是因为第 1次轮回已经确定了最后一个格子的元素,所以不用再比较最后两个元素了。
第 3次轮回,只比较 2次;第 4次,只比较 1次。
算起来就是:4 + 3 + 2 + 1 = 10 次比较。
推广到 N个元素,需要
(N -?1) + (N -?2) + (N -?3) + … + 1 次比较。
分析过比较之后,再来看看交换。
如果数组不只是随机打乱,而是完全反序,在这种最坏的情况下,每次比较过后都得进行一次交换。因此N个元素需要(N -?1) + (N -?2) + (N -?3) + … + 1 次交换。
那么总共花费的步数为:比较数*交换数,即
[?(N -?1) + (N -?2) + (N -?3) + … + 1 ] * 2
运用数学知识计算可得结果为 N^2/2-N+1/2,保留最高次为N^2

因此描述冒泡排序效率的大 O记法,是 O(N^2)。
O(N^2)算法是比较低效的,随着数据量变多,其步数也剧增,如下图所示。

最后一点:O(N^2)也被叫作二次时间。
5.二次问题
假设我们现在要写一个函数来检查数组中是否有重复值。
首先想到的可能是这样的循环嵌套:
bool CheakDUP(int arr[], int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
//有重复值返回true
if (i != j && arr[i] == arr[j])
{
return true;
}
}
}
//没有返回false
return false;
}此函数运用了两层循环进行比较,其中 i 先指向一个数字不动,然后让 j 从开头走到最后并比较以它俩为索引处的值。如果相同就返回 true 。
我们考虑最坏情况,N个元素的数组中的每个元素都俩俩比较过,所花费的步数为 N^2。
此函数所用算法的时间复杂度为O(N^2)。
虽然 CheakDup 是我们目前唯一想到的解决方法,但在确定采用之前,应意识到它的 O(N^2 )意味着低效。当遇到低效的算法时,我们都应该花些时间思考下有没有更快的做法。特别是当数据量巨大的时候,优化不足的应用甚至可能会突然挂掉。尽管这可能已经是最佳方案,但你还是要确认一下。
6.线性解决
以下是 CheakDup 的另一种实现,它没有嵌套循环。看看它是否会比之前的更加高效。
bool CheakDUP(int arr[], int n, int MAX)
{
int existingnums[MAX] = { 0 };//MAX为数组中最大的值;将数组初始化为0
for (int i = 0; i < n; i++)
{
if (existingnums[arr[i]] == 0)//如果该位置为0,则说明此处此索引所对应的数字并未重复
{
existingnums[arr[i]] = 1; //将0改为1做为标记
}
else //若该索引处的值不为0,则说明之前已被标记。即意味着有重复值
{
return true;
}
}
return false;
}此次我们只用了一层循环便解决了问题。其原理为,以原数组arr中的值为新数组existingnums的索引,并通过该索引将该索引处的值改为1,也就是标记此处已被占用。
若下一次又通过新的索引找到了该位置,并且发现该位置已被标记(指0变为1)那么就意味着该索引为重复值。
同样的,最坏的情况就是无重复,因为你得跑完整个循环才能发现。可见 N 个元素就要 N 次比较。因为这里只有一个循环,数组有多少个元素,它就要迭代多少次。
因此其大 O记法是 O(N)。
我们知道 O(N)远远快于 O(N^2 ),所以采用第二种算法能极大地提升 CheakDup的效率。如果这个程序处理的数据量很大,那么性能差别是很明显的(其实第二种算法有一个缺点,不过我们在最后一章才会讲到)。
7.总结
毫无疑问,熟悉大 O记法能使我们发现低效的代码,有助于我们挑选出更快的算法。然而,偶尔也会有两种算法的大 O相同,但实际上二者快慢不一的情况。下一章我们就来学习当大 O记法太过粗略的时候,如何识别两种算法的效率高低。
本章完!?