54 三数之和

首先想到的就是之前的两数之和,只要在外层遍历一遍,对每个元素用之前的两数之和的哈希做法,就刚好是O(n^2)
但是有坑的地方在于需要去重,并且输出的三元组也是需要顺序的!!然后我用set去重和重写比较器花了较多时间
import java.util.*;
public class Solution {
public ArrayList<ArrayList<Integer>> threeSum(int[] num) {
//固定一个之后就是两数之和
ArrayList<ArrayList<Integer>>res = new ArrayList<ArrayList<Integer>>();
Set<ArrayList<Integer>> s = new HashSet<ArrayList<Integer>>();
for(int i=0;i<num.length;i++){
Map<Integer,Integer> p = new HashMap<>();
int sum=-1*num[i];
for(int j=i+1;j<num.length;j++){
if(p.containsKey(num[j])){
ArrayList<Integer> row = new ArrayList<Integer>();
row.add(num[i]);
row.add(sum-num[j]);
row.add(num[j]);
row.sort((a,b)->a-b);
s.add(row);
}
if(!p.containsKey(sum-num[j])){
p.put(sum-num[j],j);
}
}
}//用set去重
for(Iterator<ArrayList<Integer>> i=s.iterator();i.hasNext();){
res.add(i.next());
}
//三元组也要排序输出
Collections.sort(res,new Comparator<ArrayList<Integer>>(){
@Override
public int compare(ArrayList<Integer> o1, ArrayList<Integer> o2) {
for(int i=0;i<3;i++){
if(o1.get(i)!=o2.get(i))
return o1.get(i)-o2.get(i);
}
return 0;
}
});
return res;
}
}
学到的:set的遍历:
for(Iterator<ArrayList<Integer>> i=s.iterator();i.hasNext();){
res.add(i.next());
}
比较器的自定义:
Collections.sort(res,new Comparator<ArrayList<Integer>>(){
@Override
public int compare(ArrayList<Integer> o1, ArrayList<Integer> o2) {
for(int i=0;i<3;i++){
if(o1.get(i)!=o2.get(i))
return o1.get(i)-o2.get(i);
}
return 0;
}
});
注意这里是直接返回 o1.get(i)-o2.get(i);,如果是降序排列就是 o2.get(i)-o1.get(i);!!!compare的返回值如果为负数,表示不用交换o1和o2,如果为正再交换。不用if判断!!!
55没有重复项数字的全排列

这道题知道要递归也不知道怎么写,一开始看了很久的题解还是没理解,最后还是看了深搜的回溯算法才最终理解:
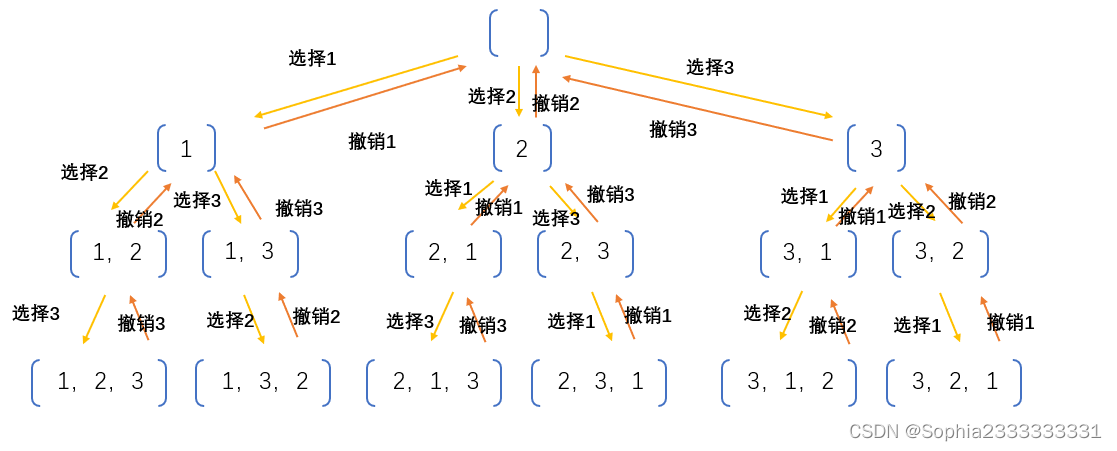
比如我现在要往3个盒子里填3个数字,全排列的话,用dfs,参数index表示我当前要添入的盒子的下标(0,1,2)
递归需要边界条件和当前处理逻辑:
边界条件:已经全部填完,当前索引==num.size
当前逻辑:遍历所有元素,如果还没放到盒子中,就放入,递归到放index+1个空盒子
最重点在于回溯:满了之后就从末尾撤回一个,才能尝试其他可能
import java.util.*;
public class Solution {
ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
ArrayList<Integer> list = new ArrayList<Integer>();
public ArrayList<ArrayList<Integer>> permute(int[] num) {
dfs(num,0);
return res;
}
public void dfs(int[] num,int index){
//递归结束条件
if(index==num.length){
res.add(new ArrayList<Integer>(list));//重点!!
return;
}
//递归执行
for(int i=0;i<num.length;i++){//遍历所有元素 不是从i=index开始
if(list.contains(num[i])) continue;
list.add(num[i]);
dfs(num,index+1);
//回溯:撤销末尾的
list.remove(list.size()-1);//注意不是remove(num[i])
}
}
}
除了算法,用java实现也有几个要注意的地方:
1.res.add(new ArrayList(list));//添加进res的时候要复制一个新list,否则直接res.add(list),始终是同一个list对象,后面的list的各种操作还会体现到res里,这显然不是我们要的!!
时间复杂度:O(n?n!)O(n*n!)O(n?n!),n个元素的数组进行全排列的递归,每次递归都要遍历数组
空间复杂度:O(n)O(n)O(n),递归栈的最大深度为数组长度n,res属于返回必要空间
55有重复项数字的全排列

思想和上题一样,只是多存了一个count数组记录每个元素对应的个数
import java.util.*;
public class Solution {
int[] count = new int[8];//存-1 5对应数字个数 -1 5映射到index 1 7 全局默认初始化为0
ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
ArrayList<Integer> list = new ArrayList<Integer>();
//去掉重复的
HashSet<ArrayList<Integer>> set = new HashSet<ArrayList<Integer>>();
public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) {
for(int i=0;i<num.length;i++) count[num[i]+2]++;
dfs(num,0);
for(Iterator<ArrayList<Integer>> it=set.iterator();it.hasNext();){
res.add(it.next());
}
//字典序排列输出
Collections.sort(res,new Comparator<ArrayList<Integer>>(){
@Override
public int compare(ArrayList<Integer> a, ArrayList<Integer> b){
for(int i=0;i<a.size();i++){
if(a.get(i)!=b.get(i)) return a.get(i)-b.get(i);
}
return 0;
}
});
return res;
}
public void dfs(int[] num, int index){
if(index==num.length){
set.add(new ArrayList<Integer>(list));
return;
}
for(int i=0;i<num.length;i++){
if(count[num[i]+2]>0){
list.add(num[i]);
count[num[i]+2]--;
dfs(num,index+1);
list.remove(list.size()-1);
count[num[i]+2]++;
}
}
}
}