文章目录
前言
我们终于进入数据结构的阶段了,在这个阶段,我们就正式开始程序员的道路了,兴不兴奋,开不开心呢?当然了,我们在开始学习之前,我们会学习一下基本的概念和术语,大家也不要心急,这也是一个漫长的过程。
一. 基本的概念和术语
1.1 什么是数据
数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识
别,并输入给计算机处理的符号集合 数据不仅仅包括整型、实型等数值类型,还包
括字符及声音、图像、视频等非数值类型。
比如我们现在浏览的一些网页,看到的一些视频,听到的一些音乐,这些都是数据。
但是我们所说的数据必须满足俩个条件,一个是可以输入计算机的 第二个是 能被计算机程序处理的。
1.2 数据元素
数据元素是组成数据的、有一定一一的基本单位,在计算机中通常组偶为整体的处理,也被称之为数据。
那么什么是数据元素呢?比如说人类中,人就是数据元素,动物中,老虎,狗,猫这些东西就是数据元素。
1.3 数据项
数据项:一个数据元素可以由若干个数据数据项组成。
比如人这样的数据元素,可以有眼、耳、鼻、嘴 手、脚这些数据项,也可以有
姓名、年龄、性别、出生地址、联系电话等数据项,具体有哪些数据项,要视你做的
系统来决定。
我们在数据结构当中数据项就是数据不可分割的最小单位。
1.4 数据对象
数据对象:是性质相同的数据元素的集合,是数据的子集
什么叫性质相同呢,是指数据元素具有相同数量和类型的数据项,比如,还是刚才的例子,人都有姓名、生日、性别等相同的数据项。
既然数据对象是数据的子集,在实际应用中,处理的数据元素通常具有相同性质在不产生混淆的情况下,我们都将数据对象简称为数据
好了,有了这些慨念的铺垫,我们的主角登场了。
说了数据的定义,那么数据结构中的结构又是什么呢?
1.5 数据结构
从字面上去理解的话,数据结构是什么?结构简单的理解就是管理,在现实世界中,不同的数据元素之间不是独立的,而是存在的特定关系,我们将这些关系称之为结构。那么数据结构是什么呢?书中给出解释是:是相互之间存在的一种或多种特定关系的数据元素的集合。当然我们为编写出一个 好"的程序,必须分析待处理对象的特性及各处理对象之间存在的关系。这也就是研究数 结构的意义所在。
1.6 逻辑结构和物理结构
我们根据视角的不同,我们把数据结构分为逻辑结构和物理结构
1.6.1 逻辑结构
逻辑结构:是指数据对象中数据 素之间的相互关系。其实这也是我 今后最需
要关注的问题 逻辑结构分为以 四种:
1. 集合结构
集合结构:集合结构中的数据 素除 同属于一个集合外,宫们之 没有其他关
系。
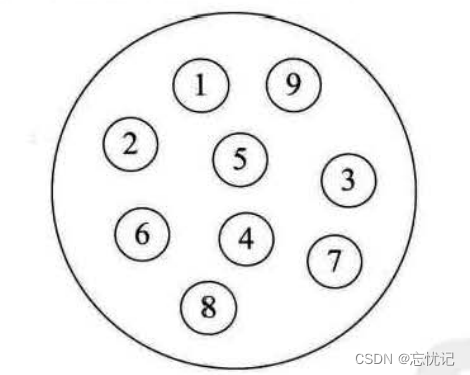
2. 线性结构
线性结构:线性结构中的数据元素之间是一对一的关系。
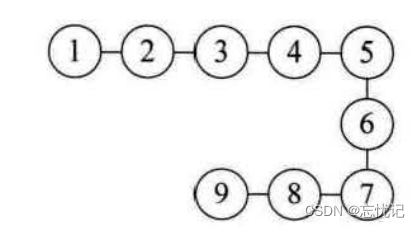
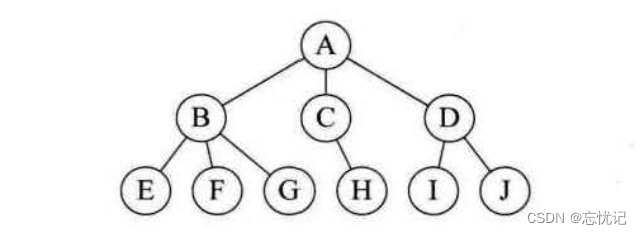
3. 树形结构
树形结构:树形结构中的数据元素之间存在一种 对多的层次关系
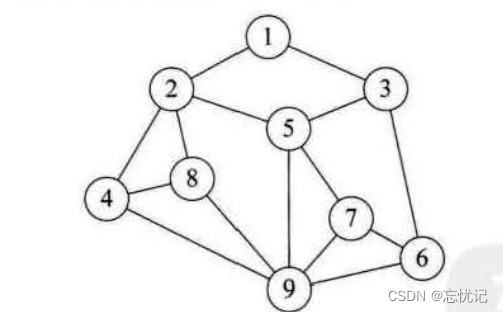
4. 图形结构
图形结构:图形结构的数据元素是多对多的关系
1.6.2物理结构
物理结构就是指数据的逻辑结构在计算机中的存储形式。我们简单的把它分为俩种
1. 顺序存储结构

2. 链式存储结构
总的来说逻辑结构就是面向问题的,而物理结构就是面向计算机的,其根本的目的就是将数据及其逻辑关系存储到计算机内存中。
二. 算法
这咋就突然跳到算法的层次,很多人又要讲了,究竟是了解数据结构还是算法,其实数据结构和算法本身就是密不可分的东西。我们要说数据结构,那就必然要说算法这个东西。
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
因此我们学数据结构,就是要结合算法来进行深入学习的。
2.1 算法的特性
算法具有五个基本特性:输入、输出、有穷性、确定性和可行性。
当然这里我就简要的罗列一下这些概念性的东西。
- 输入、输出:
算法具有零个或多个输入。尽管对于绝大多数算
法来说,输入参数都是必要的,但对于个别情况,如打印 hello wo ld 这样的代
码,不需要任何输入参数 算法的输入可以是零个。 算法至少有一个或多个输
出, 算法是一定需要输出的,不需要输出,你用这个算法干吗?输出的形式可以是打
印输出,也可以是返回一个或多个值等
- 有穷性
有穷性:指算法在执行有限的步 之后,自动结束而不会出现无限循环,并且每一个步骤在可接受的时间内 。
- 确定性
算法的每一 骤都具有确定的含义,不会出现二义性。
- 可行性
算法的每 步都必须是 行的 也就是说,每 步都能够通过执行有限
次数完成。
2.2 算法设计的要求
- 正确性
- 可读性
- 健壮性
- 时间效率高和存储量低
2.3 衡量算法的效率的方法。
我们终于进入重头戏了,怎么说呢?我们怎么去衡量一个算法的好坏呢?一般来说我们一开始想到的就是时间,执行的时间短,那么就说这个算法效率高,但是时间现在确实不能用来衡量一个算法的优劣了,为什么这么说呢?假如,我有一个求阶乘的函数如下:
public static void test15(){
//计算公式:n!=n*(n-1)! 1*2*3*4*5
int num = 1; //从1开始
for (int i = 1; i <=5; i++) { //不是事0
num=num*i;
}
System.out.println("5的阶乘是"+num);
}
假如我输入100万,那么根据时间去判断这个程序的效率真的合适吗?假如我们测试的机器不一样呢?我一个老机器和一个现代新机器去运行这个程序,执行的效率肯定就不一样,我的电脑配置拉满,你的电脑就是个老古董,去用时间去衡量程序的好坏,显然是不可取的,因此我们就引入了时间复杂度和空间复杂度去衡量一个算法的优劣。这些东西是什么,接下来我会逐一去介绍。
2.3.1 时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算
法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
我们这里说的时间复杂度,是最坏情况的时间复杂度哦
于是我们怎么去计算呢?
这个时候,又引进了一种新的方法,去计算时间复杂度,就是大O表示法。现将推导大O阶方列出:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
大家记住以上三点就知道怎么去计算时间复杂度了,不信的话我们举几个例子,你就明白了。
第一个
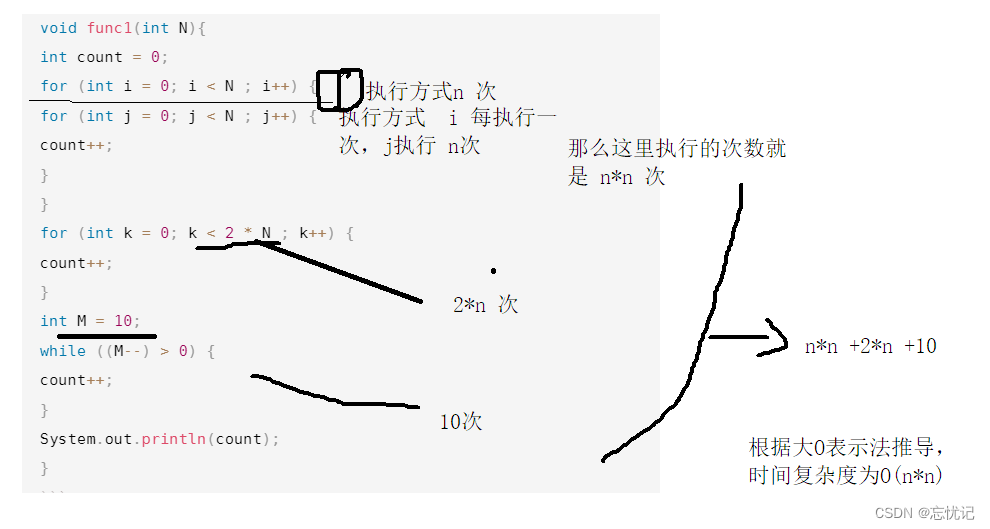
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}
第二个
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}

第三个
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}

第四个
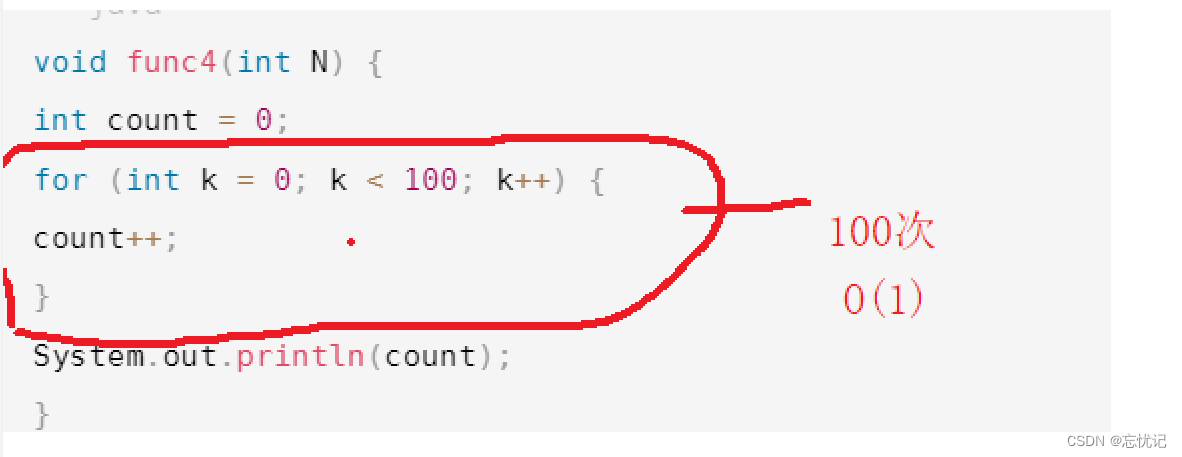
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}
第五个
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}

第六个
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}

第七个
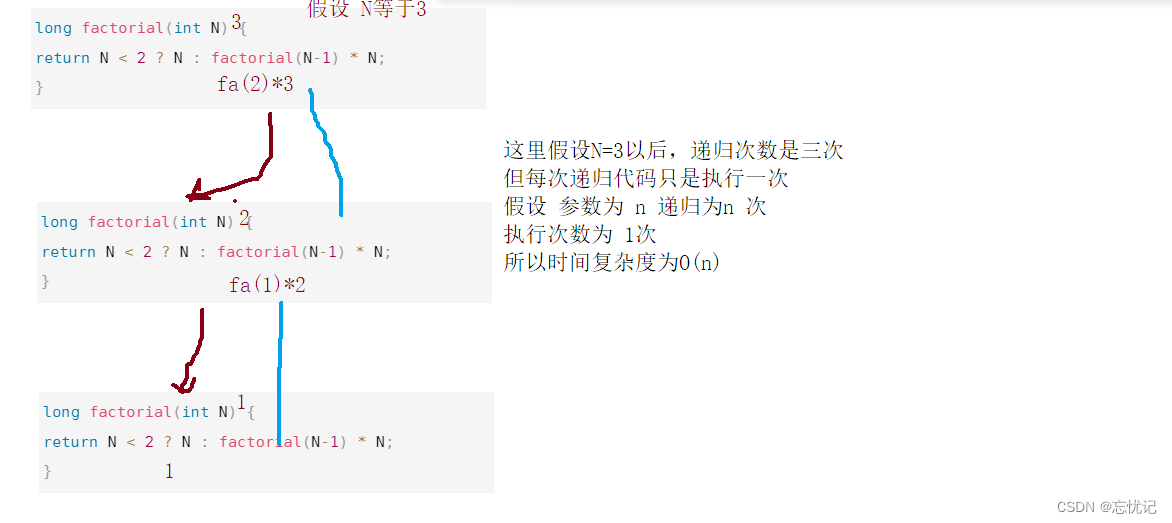
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}
这个程序就跟之前的几个不一样了,这里就涉及了递归程序,跟之前的顺序结构和循环结构不一样,我们简单的总结一下递归的时间复杂度的步骤。简单用几个字去总结吧,递归的时间复杂度等于递归的次数*每次递归后代码执行的次数。
第八种
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
相信大家都看得懂这个程序,这就是计算斐波那契数。我们来逐步分析一下这个程序的时间复杂度是多少。
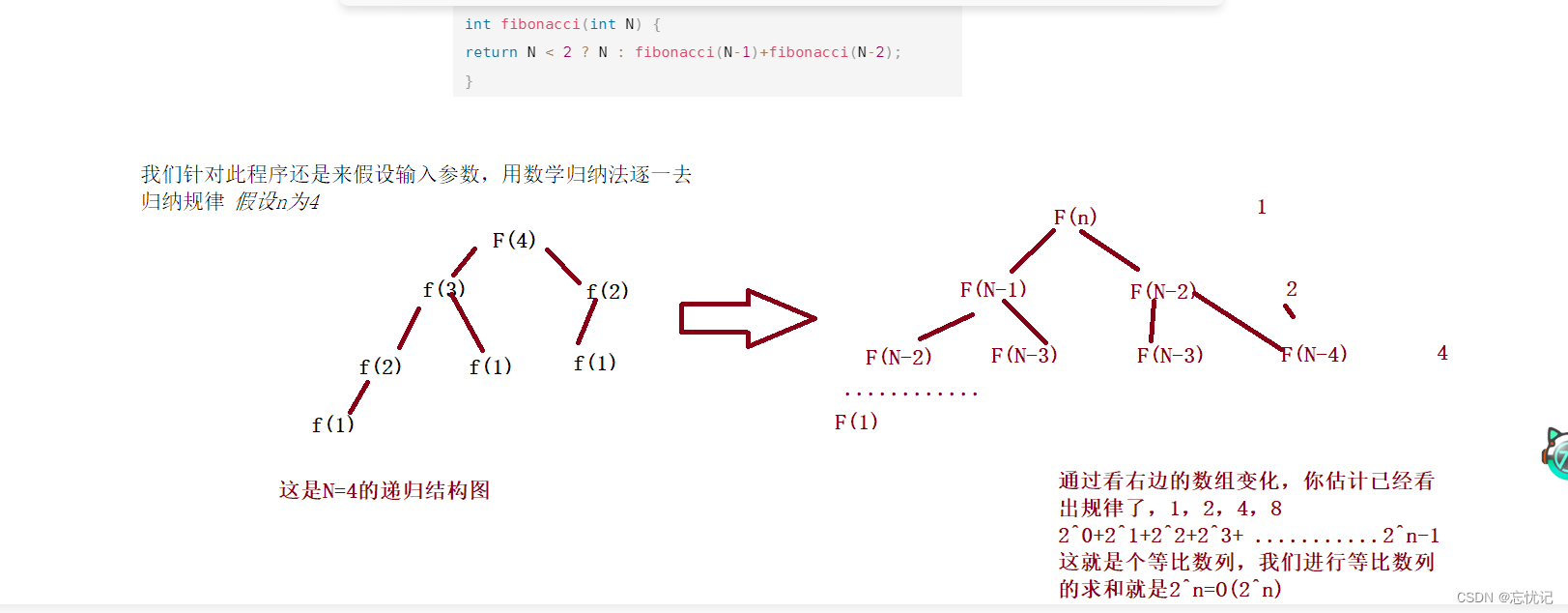
相信大家经过了这么多例子的演练,肯定对时间复杂度的计算,已经非常熟练了吧。
开始进入我们空间复杂度计算
2.3.2 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
我们还是来看例子,你就明白空间复杂度的计算了。
例子1
// 计算bubbleSort的空间复杂度?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}

例子2
// 计算fibonacci的空间复杂度?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}

例子3
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}
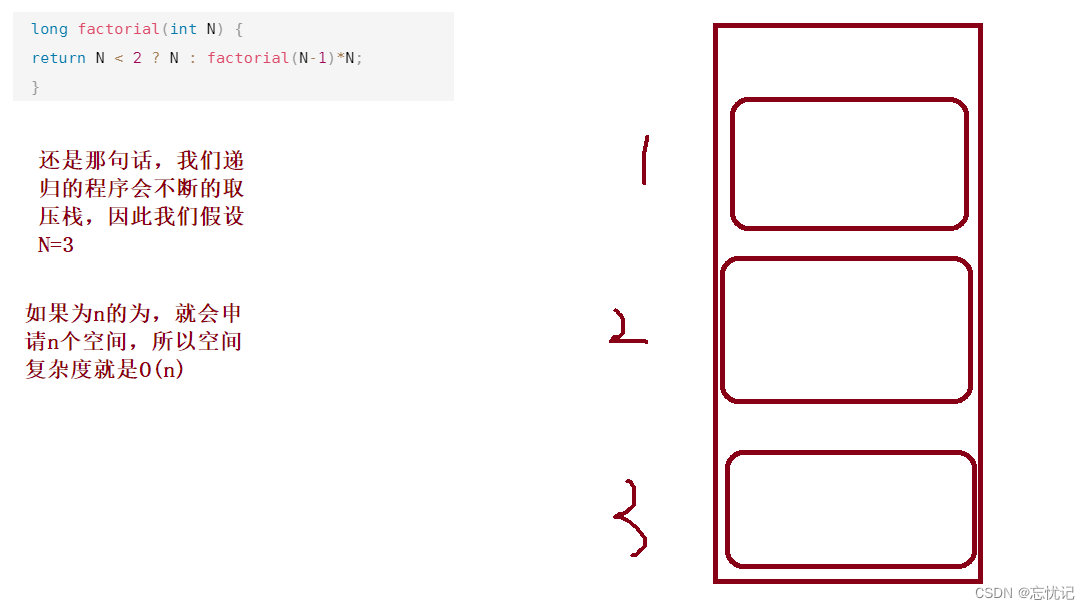
空间复杂度的例子到这里就结束,大家不要担心,后续我们每针对一个程序我们都会去分析它的时间复杂度和空间复杂度的。