坚持看完,结尾有思维导图总结
这里写目录标题
插入排序
插入排序的步骤
什么是插入排序
根据官方的说法就是
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
简单地说,就是和扑克牌排序一样
如果你抽到一张 5,首先你要找到比他小的数
如果你找到了 3 和 4
毫无疑问你要放在 4 的后面
而不是3或者6的后面。
插入排序的单趟排序
插入排序的单趟排序要实现的目标是
如果向一个有序数组中随机插入一个数,通过插入排序,能够找到这个随机数在有序数组的位置,使得整个数组重新有序
如果向一个数组
假如数组的内容是 1 3 6 10
向其中插入数字 4
单趟排序的步骤
整个过程的步骤是
1.找到最近的比 4 小的值 a
2.通过移动a后面的值来空出 a 后面的空间
3.将 4 插入到这个值后面
插入排序的图解

完整的插入排序排序
单趟的插入排序的前提,是一个有序的数组
但是随机数组不会是有序的
那应该如何解决?
我们可以利用 只有一个元素的数组来解决这个问题
在这个基础上
只有一个元素的数组是有序的
随后插入一个元素后,两个元素的数组是有序的
在不断插入,最终使得整个数组有序
假如我们要排序一个数组
22 44 23 78 66 25 85
其中红圈表示就是有序数组
插入排序的图解是?

插入排序的程序
void InsertSort(int* a,int len)
{
for(int i = 0;i<len-1;i++)
{
int end = i;
int tmp = a[end+1];
//单趟
while(end>=0 && a[end]>tmp)
{
a[end+1] = a[end];
end--;
}
a[end+1] = tmp;
}
}
插入排序的常见问题
关于 end 的是否越界的问题

由于 tmp = a[end + 1]
end = i,所以 end + 1< len ,i < ken -1
end 可以为 0 ,单插入的值比第一个值还要小的时候
end – 后,end = -1越界却没有访问
之后将 tmp 插入到 end + 1的位置,end + 1= 0,此时没有越界
关于插入排序的时间复杂度分析
希尔排序的时间复杂度
如果一个数组是倒序,这个时候是最糟糕的情况
每添加一个数据,都要拿到最前面去,然后挪动数据,此处挪动数据的次数是 n ,每个数都需要挪动,时间复杂度就是 n^2

插入排序的空间复杂度是 O(1)
插入排序的稳定性是
因为 a[end] > tmp 的 时候都直接跳过,所以最终 a[end] <= tmp
所以,如果相同的数,本身在数组之前的值依旧在数组前面,本身在数组后的值在数组后面
所以插入排序是稳定的
希尔排序
插入排序,有一个问题,他的时间复杂度来源是,当某个数很小的时候,要挪动许多数据到前方,从而导致的时间损耗
希尔排序就是为了解决这个问题
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个
组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工
作。当到达=1时,所有记录在统一组内排好序。
而除了最后的 grip = 1 的排序,之前的排序都叫预排序
希尔排序的图解
简单地说
如果有一组数,可以按照一定的步长进行分小组
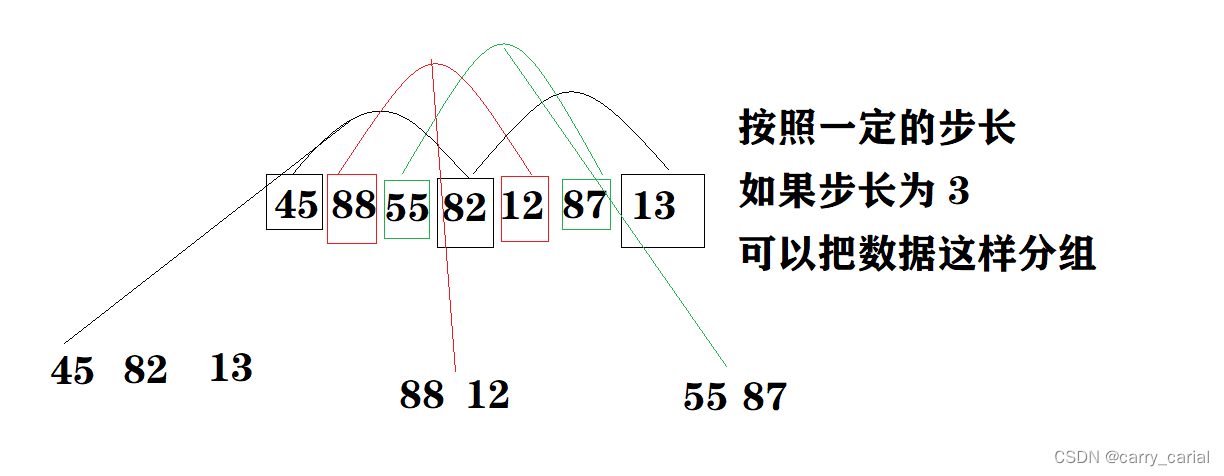
如果在小组内进行插入排序,就能实现数值小的数快速挪动到数组前面的效果
比如由黑色框构成的一组数(叫黑组)
当13 走到 45 前面,在实际数组中,13 就直接排头了

希尔排序的步骤
从图解可以提炼出步骤
1.得到步长,将数据分组
2.在组内进行插入排序
希尔排序的程序
void ShellSort(int*a,int len)
{
int grip = len;
// 设置步长,最后一次步长为1
while(grip>1)
{
grip = grip/3 + 1;
// 分出的组数和步长一致
for(int group = 0;group < grip;group++)
{
//分组插入排序
for(int i = group;i<len-grip;i+=grip)
{
int end = i;
int tmp = a[end + grip];
while(end >= 0 && a[end] > tmp)
{
a[end + grip] = a[end];
end-=grip;
}
a[end+grip] = tmp;
}
}
}
}
化简一下代码
void ShellSort(int*a,int len)
{
int grip = len;
// 设置步长,最后一次步长为1
while(grip>1)
{
grip = grip/3 + 1;
for(int i = 0;i<len-grip;i++)
{
int end = i;
int tmp = a[end + grip];
while(end >= 0 && a[end] > tmp)
{
a[end + grip] = a[end];
end-=grip;
}
a[end+grip] = tmp;
}
}
}
需要强调的问题
希尔排序中 grip 的设计和优化的问题
首先,为了保证 grip 的大小最后为1,才能保证这个数组数顺序的
站在前人的肩膀,能够知道 grip = grip /2,和 grip = grip /3 +1 是比较合理的设计
其次,每次从首元素 k 跨过 grip 的元素 k+grip 才分成相同的小组,因此从[k , k+grip) 的元素中都是不同组的,所以 group 的数量为 grip
因为 tmp = a[end + grip ] 所以不能越界,最后 end 只能为 len - grip,再向后就越界了
关于优化前后的代码
优化前后的原理是等等效的,只是顺序不一样而已
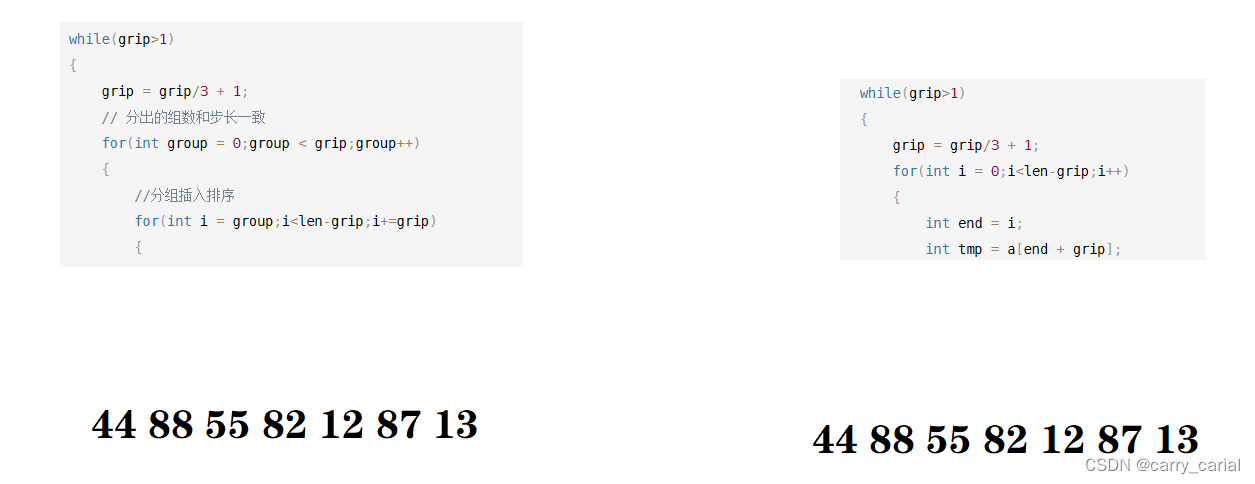
左边的代码是先分组,然后再进行插入排序
右边的代码时边分组,边插入排序
最终的结果相同

总结
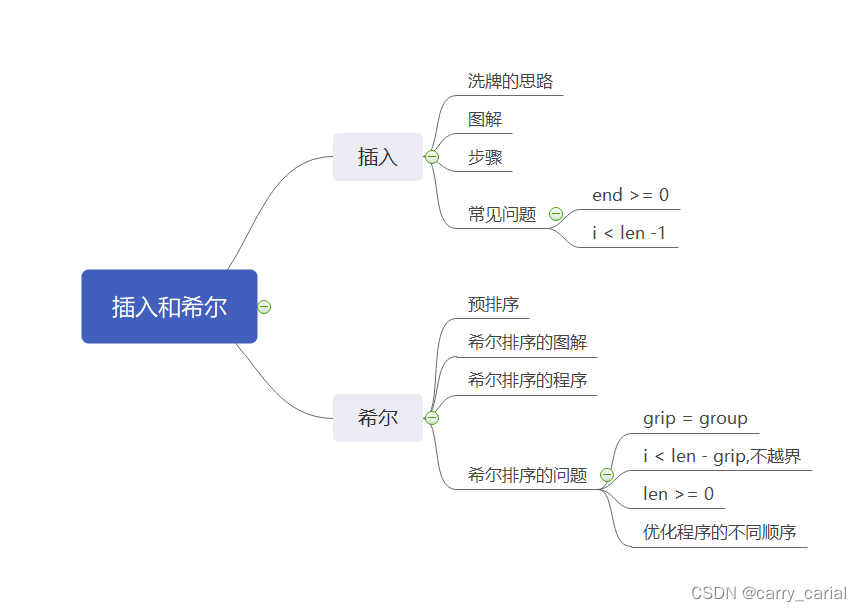
希望大家看完,能够有所收获
如果有错误,请指出我一定虚心改正
动动小手点赞
鼓励我输出更加优质的内容