开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【计算机考研408】数据结构代码规范 -> 正文阅读

[数据结构与算法]【计算机考研408】数据结构代码规范

408-数据结构代码规范

文章目录

408-数据结构代码规范

序言

自用。
本文目的不在于分析题目的解法，而在于规范代码的格式

优化

算法思想类型的代码尽可能靠近

参考文献

1 408算法题源 https://leetcode.cn/circle/discuss/3qmfV0/

考前预测

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head == NULL) return NULL;
        //头插法
        ListNode * p = head;//工作指针，指向链表的最后一个位置，由于leetcode没有头结点后面相当于把最后一个结点当作头结点使用
        ListNode * q = head;
        while(p->next != NULL){
            p = p->next;
        }
        
        //开始头插
        //工作指针
        p->next = NULL;
        ListNode *r;
        while(q != p){
            r = q->next;
            q->next = p->next;
            p->next = q;
            q = r;
        }
        return p;
    }
};

注意：别让链表成环了

线性表-链表

单链表

typedef struct LNode{
    ElemType data;
    struct Lnode *next;
} LNode, *LinkList;

注：双链表则添加一个指针prior指向前面一个结点

静态链表

#define MaxSize 50
typedef struct{
    ElemType data;
    int next;
} SLinkList[MaxSize];

注：next==-1作为其结束标志

栈、队列、数组

栈的顺序存储类型

#define MaxSize 50
typedef struct{
    ElemType data[MaxSize];
    int top;//栈顶指针
}sqStack;

注：栈顶指针S.top，初始时设置S.top = -1; 栈顶元素 S.data[S.top];
显然，入栈先加1.再赋值，而出栈先取值，再减1

S.top == -1; //栈空条件 
S.top == MaxSize - 1; //栈满条件
int L = S.top + 1; //栈长

队列

#define MaxSize 50
typedef struct{
    ElemType data[MaxSize];
    int front;//队头指针
    int rear;//队尾指针
} queue;

树与二叉树

二叉树的定义

typedef struct BitNode{
    ElemType data;
    struct BitNode *lchild, *rchild;
}BitNode, *BitTree;//一个是结点的声明，一个是指针的声明

二叉树的层序遍历

void LevelOrder(BitTree T){
	InitQueue(Q);
    BitTree p;
    EnQueue(Q, T); //根结点入队
    while(!Q.isempty()){
        DeQueue(Q, p);
        visit(p);
        if (p->lchild != NULL){
            EnQueue(Q, lchild);
        }
        if (p->rchild != NULL){
            EnQueue(Q, rchild);
        }
    }
}
//注：使用stl的代码会更为简洁，内容也没有差距，但还是以王道书（来源考纲）命名为主

树的双亲表示法

如何记忆：用于表示多叉树+双亲

也可以表示森林

#define MaxTreeSize 100
typedef struct{
    ElemType data;
    int parent;
}PTNode;

typedef struct{
    PTNode nodes[MaxTreeSize];
    int n;
}PTree;

孩子表示法

可以用来表示多叉树

//下一个孩子的信息
typedef struct Child{
    int index; //孩子编号
    struct Child *next; //下一个孩子
} Child;

//TreeNode 用于保存结点信息
typedef struct TreeNode{
    char data;
    Child* firstChild;
}TreeNode;

TreeNode tree[10];

树的孩子兄弟表示法

可以借助多叉树化二叉树的思想记忆

typedef struct CSNode{
    ElemType data;
    struct CSNode *firstchild, *nextsibling;//第一个孩子和右兄弟指针
}

图

邻接矩阵存储法

#define MaxVertexNum 100 //顶点数目
typedef struct{
    char v[MaxVertexNum]; //顶点表
    EdgeType e[MaxVertexNum][MaxVertexNum]; //边表
    int vnum, arcnum //顶点个数
} MGraph;

邻接表法

略，考察可能性不大

二分查找/折半查找

模板

start为第一个元素所在位置下标
end为最后一个元素所在下标

int binary_search(int low, int high, int key) {
  int ret = -1;  // 未搜索到数据返回-1下标
  int mid;
  while (low <= high) {
    mid = (low + high) / 2;
    if (arr[mid] < key)
      low = mid + 1;
    else if (arr[mid] > key)
      high = mid - 1;
    else {  // 最后检测相等是因为多数搜索情况不是大于就是小于
      ret = mid;
      break;
    }
  }
  return ret;  // 单一出口
}

优化

int binary_search(int start, int end, int key) {
  int ret = -1;  // 未搜索到数据返回-1下标
  int mid;
  while (start <= end) {
    mid = start + ((end - start) >> 1);  // 直接平均可能会溢出，所以用这个算法
    if (arr[mid] < key)
      start = mid + 1;
    else if (arr[mid] > key)
      end = mid - 1;
    else {  // 最后检测相等是因为多数搜索情况不是大于就是小于
      ret = mid;
      break;
    }
  }
  return ret;  // 单一出口
}

区间划分

前言，每种区间划分所导致代码都会有细节上的不同。

假设，区间长度为 [L, R]

划分1

将[L, R]区间可以划分为[L, mid], [mid+1, R]，那么对应的更新就应该为

R = mid;
L = mid + 1;

快速排序

基于分治的思想，主要由两个步

1）划分

2）排序

代码

void quicksort(int a[], int low, int high){
	if (low < high){
        int pos = partition(a, low, high);
    	quicksort(a, low, pos-1);
        quicksort(a, pos+1, high);
    }
}
//partition是一趟排序
int partition(int a[], int low, int high){
    int pos = a[low];//将表中第一个元素设置位枢轴
    while(low < high){
        //从右边找到第一个比枢轴值小的
        while(low < high && a[high] >= pos) --high;
        a[low] = a[high];
        while(low < high && a[low] >= pos) ++low;
        a[high] = a[low];
    }
    a[low] = pos;
    return low;
}

分析

不稳定
受初始序列的排序的影响
在平衡的划分下，效率高，【选择题考察】
快速排序最坏情况下O(n^2)平均情况下O(nlog2n)

归并排序

代码

int *b = (int *) malloc (sizeof(int) * (n+1));
void merge(int a[], int low, int mid, int high){
    //表的两段各自有序将其进行合并
    for(int i = low; i <= high; i++){
        b[i] = a[i];
    }
    int i, j, k;
    for(i = low, j = mid+1, k = 0; i <= mid && j <= high; k++){
        if (b[i] <= b[j]){
            a[k] = b[i++];
        }
        else {
            a[k] = b[j++];
        }
    }
    while(i <= mid){
        a[k++] = b[i++];
    }
    while(j <= high){
        a[k++] = b[j++];
    }
}
void mergesort(int a[], int low, int high){
    if (low < high){
        int mid = (low + high) / 2;
        mergesort(a, low, mid);
        mergesort(a, mid+1, high);
        merge(a, low, mid, high);
    }
}`

分析

空间复杂度O(n)
时间复杂度O(nlog2n)
稳定的排序方法
与初始序列的排列无关

2009年-链表中倒数第k个节点

题目

给你一个链表要你得到倒数第k个数字

题解

双指针移动，第一个指针与第二指针的距离为k，当第一个指针到达最后的位置的时候，第二个指针恰好在倒数第k个位置上。

代码

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode * pre = head;
        ListNode * pos = head;
        int cnt = 0;
        while(pre != NULL){
            if (cnt < k){
                pre = pre->next;cnt++;
            }
            else {
                pre = pre->next;
                pos = pos->next;
            }
        }
        return pos;
    }
};

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        int len = 0;
        ListNode * tmp = head;
        for(; tmp!=NULL; tmp=tmp->next, len++);
        for(int i = 0; i < len - k; i++, head = head->next);
        return head;
    }
};

2010年-旋转数组

题目

将数组nums向右移动k个位置。

题解

方法一空间复杂度o(n),时间复杂度o(n)

每移动k次实际上是没有发生变化的，所以需要取余

k = k % size;

先取出最后的k个数字,然后将前面的数字全部后移，最后将k个数字放在前面。

方法二时间复杂度o(n) 空间复杂度o(1)

进行翻转

先翻转（0，s)

再翻转（0，k)

最后翻转（k， s)

reverse 翻转的实际上翻转的范围是 [first,last)

时间复杂度O(n)，空间复杂度O(1)

代码

408答案中从即使是p，n-1的翻转也是从0开始的，可能是有点问题的。

//实现翻转，与下面leetcode题解代码无关
void reverse(int arr[], int n, int a, int b){
	for (int i = a, j = 0; i < (b + a)/2; ++i, j++)
	{
		//swap
		int temp = arr[i];
		arr[i] = arr[b - j];
		arr[b - j] = temp;
	}
}

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        vector<int> temp;
        int s = nums.size();
        k = k % s;
        reverse(nums.begin(), nums.end());
        reverse(nums.begin() + k, nums.end());
        reverse(nums.begin(), nums.begin() + k);
    }
};

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        vector<int> temp;
        int s = nums.size();
        k = k % s;
        for(int i = s - k; i <= s - 1; i++){
            temp.push_back(nums[i]);
        }
        for(int i = 0; i < s - k; i++){
            temp.push_back(nums[i]);
        }
        for(int i = 0; i < s; i++) nums[i] = temp[i];
    }
};

2011年-寻找两个正序数组的中位数

题目

题解

归并

2017年-二叉树的遍历

题目

请设计一个算法，将给定的表达式树（二叉树）转换为等价的中缀表达式（通过括号反映操作符的计算次序）并输出。例如，当下列两棵表达式树作为算法输入时：

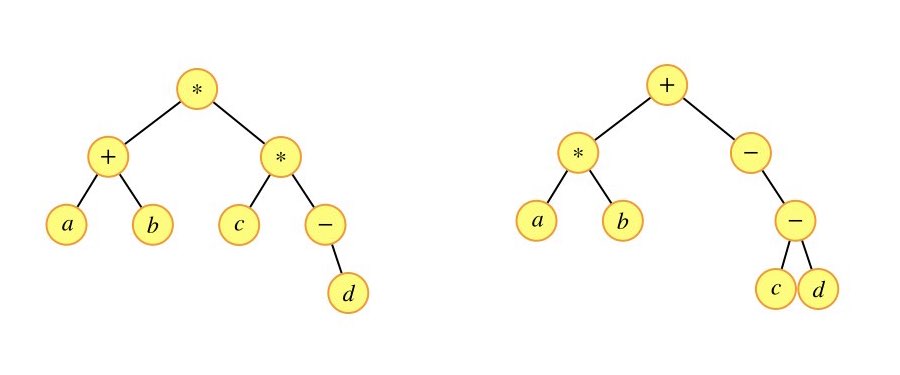
输出的中缀表达式分别为 (a+b)?c(c?(?d)) 和 (a?b)+(?(c?d)) 。

二叉树结点的定义如下：

typedef struct node{ 
    char data[10];   //存储操作数或操作符
    struct node *left, *right;     
}BTree;

要求：

⑴ 给出算法的基本设计思想。

⑵ 根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

题解

掌握二叉树的遍历，以及运算式的中缀表达式。
二叉树结点的定义（这个也可能成为考题的考察点）。
结果输出的是字符串，注意字符串的输出（细节，可能不会扣分但是也要注意）。
难点在于添加左括号与右括号的位置。

代码

void Slove(BTree *root){
    InOrder(root, 1);
}
void InOrder(BTree *root, int deep){
	if (root == NULL) return ;
    else if (root->left == NULL && root->right == NULL){
        printf("%s", root->data);
    }
    else {
        //利用deep 这里处理的既不是叶子节点也不是根节点
        if(deep > 1){
            printf("(");
        } //相当于访问左子树，此处左子树添加括号了
        InOrder(root->lef, deep + 1);
        printf("%s", root->data);
        InOrder(root->right, deep + 1);
        if(deep > 1){
            printf(")");
        }
    }
}

2012年-最佳归并树与哈夫曼树

注：本处不提供真题的解答代码，仅提供归并排序的代码，理解归并思想

归并排序代码

int *b = (int *) malloc (sizeof(int) * (n+1));
void merge(int a[], int low, int mid, int high){
    //表的两段各自有序将其进行合并
    for(int i = low; i <= high; i++){
        b[i] = a[i];
    }
    int i, j, k;
    for(i = low, j = mid+1, k = 0; i <= mid && j <= high; k++){
        if (b[i] <= b[j]){
            a[k] = b[i++];
        }
        else {
            a[k] = b[j++];
        }
    }
    while(i <= mid){
        a[k++] = b[i++];
    }
    while(j <= high){
        a[k++] = b[j++];
    }
}
void mergesort(int a[], int low, int high){
    if (low < high){
        int mid = (low + high) / 2;
        mergesort(a, low, mid);
        mergesort(a, mid+1, high);
        merge(a, low, mid, high);
    }
}

分析

空间复杂度O(n)
时间复杂度O(nlog2n)
稳定的排序方法
与初始序列的排列无关

2012年-字符串匹配（链表的访问）

注意链表的定义与从哪个位置开始对比即可

typedef struct LNode{
    ElemType data;
    struct Lnode *next;
} LNode, *LinkList;

2013年-寻找主元素（栈的处理思想）

题解

如果一个序列中的某个元素个数大于n/2，那么完全足够与与其不同的元素逐一相消。

一般来说，是用栈处理，相同入栈，不同出栈，但本题要求高效，所以不用栈处理，但思想上是一致的。

代码

int FindMajority(int a[], int n){
    int res = -1;
    int top = a[0]; //第一个元素入栈
	int cnt = 0; //记入栈顶元素个数
    for(int i = 1; i < n; i++){
        if (a[i] == top){
            cnt++;
        }
        else {
            if (cnt > 0){
                cnt--;
            }
            else {
                //说明当前栈顶无主元素，那么更换主元素
                top = a[i];
                cnt = 1;
            }
        }
    }
    
    int count = 0; //统计栈顶元素实际出现个数
    for(int i = 0; i < n; i++){
		if (top == a[i]){
            count++;
        }
    }
    if (count > n/2){
        return top;
    }
    else {
        return -1;
    }
}

时间复杂度O(n)空间复杂度O(1)

2014年-计算二叉树的WPL（二叉树遍历）

题解

利用全局变量记录二叉树的wpl，先序遍历即可。

代码

typedef struct BiTNode{
	int weight;
	struct BiTNode* lchild, *rchild; 
} BiTNode, *BiTree;

int wpl = 0;//全局变量用于记录二叉树的wpl

void preorder(BiTree * T, int deep){
	if (T->lchild == NULL && T->rchild == NULL){
		wpl += T->weight * deep;
	}
	if (T->lchild != NULL){
		preorder(T->lchild, deep + 1);
	}
	if (T->rchild != NULL){
		preorder(T->rchild, deep + 1);
	}
}

int PrintWpl(BiTree *T){
	//输出结果函数
	preorder(T, 0);
	printf("%d\n", wpl);
}

2018年-利用标记数组处理判断正整数是否出现过

题目

找到最小未出现正整数

题解

标记数组

代码

int FindMissMinNumber(int a[], int n){
	int *t = (int *) malloc(sizeof(int)*(n+2));
    memset(t, 0, sizeof(int) * (n+2));
    for(int i = 0; i < n; i++){
        if (a[i] >= 1 && a[i] <= n){
            t[a[i]] = 1;
        }
    }
    for(int i = 1; i <= n + 1; i++){
        if (t[i] == 0) {
            return 0*printf("%d", i);
        }
    }
}

2019年-链表逆置（头插法）

题解

可以将头插法逆置分解为以下这几个步骤

注：图示2号是要头插的第一个元素，头结点是1号

头结点断开p->next = NULL;
当q不为空结点时，说明有元素进行头插法

? (a)工作指针r指向要进行头插元素的后一个元素r=q->next;

? (b)头结点的下一个结点指向要进行头插的结点，即为q结点p->next=q;[p的值是不会在头插过程中发生改变的，头插二字也可从此理解]

? ?进行头插的结点断开q->next=NULL;

? (d)头插下一个结点q=r;

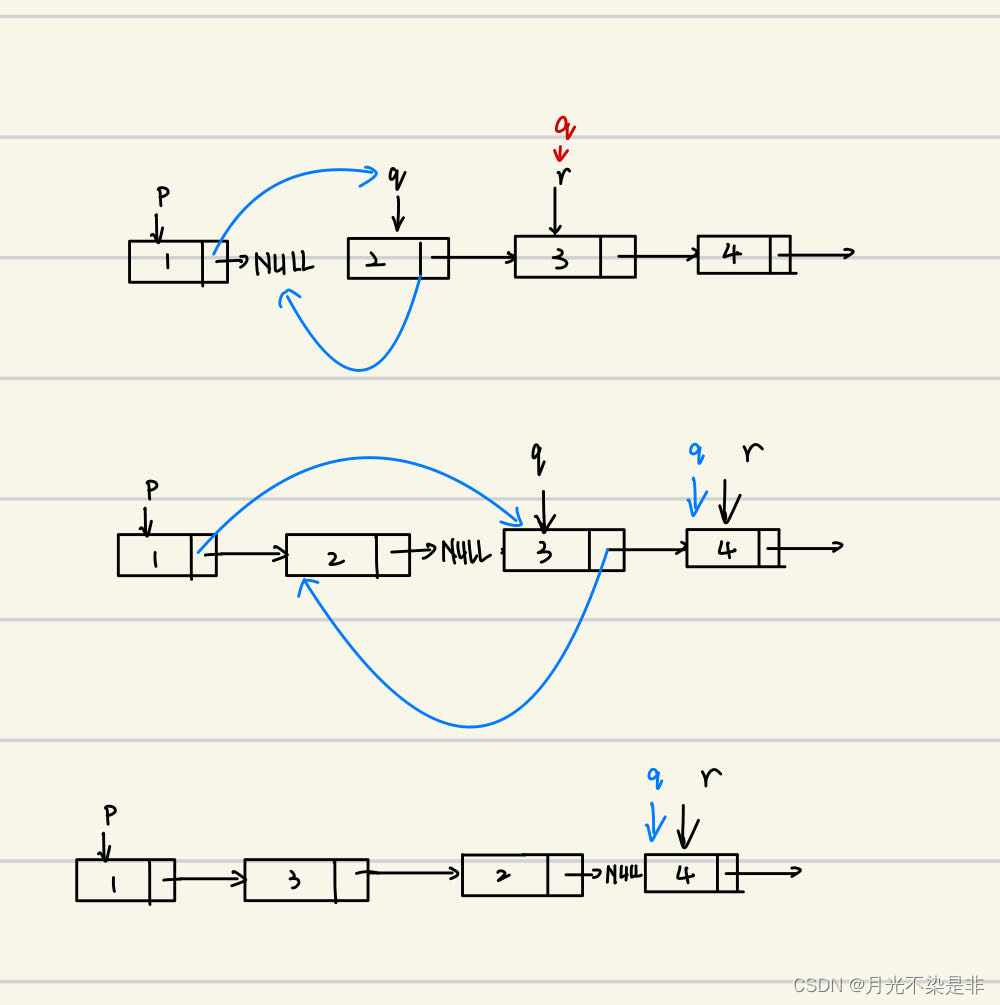
在这里插入图片描述

代码

typedef struct LNode{
    ElemType data;
    struct Lnode *next;
} LNode, *LinkList;
void slove(LinkList * h){
    LinkList *p, *q, *r, *s;//工作指针
    p = q = h;
    //寻找中间结点
    while(q->next != NULL){
        p = p->next;
        q = q->next;
        if (p->next != NULL) p = p->next;
    }
    q = p->next; //令q指向后半段首结点
    p->next = NULL;
    //将后半段链表逆置
    while(q != NULL){
        r = q->next;
        q->next = p->next;
        p->next = q;
        q = r;
    }
    
    //逐一插入即可
    s = h->next;
    q = p->next;
	p->next = NULL;
    while(q != NULL){
        r = q->next;
        q->next = s->next;
        s->next = q;
        s = q->next;
        q = r;
    }
}

2020年-求最小距离（数组的遍历）

题目

计算三元组的最小距离

题解

【答题格式】

算法的基本设计思想

（1）使用mindist记录当前所有已处理过的三元组的最小距离，初值为C语言能表示的最大整数值INT_MAX

（2）将集合S1、S2和S3的序列分别保存在数组A、B、C中。数组大小分别为m，n，p。

（3）分别定义访问数组A、B、C的三个下标变量i，j，k，初始值为0.

（4）当i<m且j<n且j<p时，循环执行（a）-（c）

? （a）计算三元组(A[i],B[j],C[k])的当前距离d

? （b）如果当前距离d<mindist，则更新，mindist=d

? （c）并将A[i],B[j],C[k]当中最小值所在数组的下标+1

（5）输出最小距离mindist

代码

算法实现

#include <limits.h>//最大int整数所在头文件
int abs(int x){
    if (x < 0) return -x;
    else return x;
}
int FindMinDist(int A[], int m, int B[], int n, int C[], int p){
    int mindist = INT_MAX;//mindist = abs(A[0]-B[0])+abs(A[0]-C[0])+abs(B[0]-C[0]);
    int i = 0, j = 0, k = 0;
    while(i < m && j < n && k < p){
        int nowdist = abs(A[i]-B[j])+abs(A[i]-C[k])+abs(B[j]-C[k]);
        if (nowdist < mindist) mindist = nowdist;
        
        if (A[i] < B[j] && A[i] < C[k]) i++;
        else if (B[j] < C[k] && B[j] < A[i]) j++;
        else k++;
    }
    return mindist;
}

时间复杂度O(n+m+p)，空间复杂度O(1)

2022年-判断是否是一棵二叉搜索树

题目

非空二叉树使用顺序存储，要求判断是否是二叉搜索树

题解

考察树就要思考树的遍历，而二叉搜索树满足左子树<根<右子树的性质，那么可以考虑中序遍历（左根右），中序遍历二叉树可以得到一个升序数列。

算法的基本设计思想

对于采用顺序存储方式保存的二叉树，根结点保存再SqBiTNode[0]中；当某结点保存在SqBiTNode[i]中时，若有左孩子，则其值保存在SqBiTNode[2*i+1]中；

若有右孩子，则其值保存在SqBiTNode[2*i+2]中；若有双亲结点，则其值保存在SqBiTNode[(i-1)/2]中。

使用整型变量val记录中序遍历过程中已遍历结点的最大值，初值可以设置为负数。若当前遍历节点的值小于等于val则说明非二叉搜索树。

否则，将val的值更新为当前结点的值。

代码

val可以设置全局变量或者调用参数。

(如果子树不是二叉搜索树的话，那么以当前结点为根的树也必定不是二叉搜索树)

bool judgeTree(SqBiTree bt, int k, int *val){
    if(k < bt.ElemNum && bt.SqBiTNode[k] != -1){
        if (!judgeTree(bt, 2*k + 1, val)) return false;
        if (bt.SqBiTNode[k] <= *val) return false;
        *val = bt.SqBiTNode[k];
        if (!judgeTree(bt, 2*k + 2, val)) return false;
    }
    return true;
}