前言
如果只需要知道某些元素是否存在于集合中,当数据量达到一定程度时(以亿级起步),搜索树、哈希表等数据结构会因为其内存占用过大而降低效率,哈希思想将映射的位置缩小到极致:将元素的存在与否以1或0映射到若干个比特位上。位图、布隆过滤器都是空间利用率和查找效率很高的数据结构。
由于实际上海量数据都是储存在数据库中的,而本文要谈论的是它本质:哈希思想。也就是位图、布隆过滤器的应用,而这也是面试中常见的类型。
注:
海量数据处理的方式不止哈希一种,作者仍在学习中,只对哈希处理海量数据作出阐述。
什么是海量数据处理
处理数据无非就是对数据进行存储和增删查改操作,而数据量一旦很大,操作起来的时间就会变长。“海量”二字可见数据量之多,要知道,我们处理数据大多数情况都是在内存中进行的,而少得可怜的内存无法储存海量数据。可见,海量数据处理主要有两个方面:
- 内存足够,时间太长:使用位图、布隆过滤器等数据结构;
- 内存不够:使用哈希切割思想,将大问题转化为小问题,分而治之。
位图的应用
题目1
给定100亿个整数,设计算法找到只出现一次的整数。
每个整数出现的次数可能是0,1,2,…100亿次,而题目只要求找到只出现1次的整数,所以可以将两个比特位作为一个整数是否存在的映射位置,用这两个比特位的二进制序列表示:
- 00:出现0次;
- 01:出现1次;
- 10:出现2次及以上。
而STL中的bitset默认以1个比特位为元素的映射位置,有两种方法:
- 人为地控制遍历时每步的跨度为2个比特位;
- 用两个位图同时记录。
下面使用第二种方法,原因是好理解,操作比较简单:
- 遍历元素,默认位置是00,第一次设置为01,第二次设置为10。
#include <iostream>
#include <vector>
#include <bitset>
#include <assert.h>
using namespace std;
int main()
{
vector<int> v{1, 3, 5, 7, 9, 2, 4, 6, 8, 10, 1, 3, 5, 7, 9};
bitset<4294967295>* bs1 = new bitset<4294967295>;
bitset<4294967295>* bs2 = new bitset<4294967295>;
for (auto e : v)
{
if (!bs1->test(e) && !bs2->test(e)) // 00->01
{
bs2->set(e);
}
else if (!bs1->test(e) && bs2->test(e)) // 01->10
{
bs1->set(e);
bs2->reset(e);
}
else if (bs1->test(e) && !bs2->test(e)) // 10->10
{
continue;
}
else
{
assert(false);
}
}
for (size_t i = 0; i < 4294967295; i++)
{
if (!bs1->test(i) && bs2->test(i)) // 01
cout << i << endl;
}
return 0;
}
输出
2
4
6
8
10
注意:
- 上面的代码只用vector里的几个样例测试,实际上是要从文件中获取数据的。
- 如果直接
bitset<4294967295>实例化位图,也就是 2 32 2^{32} 232个比特位,合计512MB,两个bitset就是1GB,这样会撑爆栈区所以使用new,让编译器在堆区申请内存。
因为一个整型变量(不论是有符号还是无符号)在32位机器下是4个字节,以unsigned类型为例,它取值范围是[0,4294967295],即[0, 2 32 2^{32} 232]。
题目2
给两个文件,分别有 100 亿个整数,只有 1G 内存,如何找到两个文件的交集?
思路1:
- 创建1个位图;
- 将第一个文件中的整数映射到位图中;
- 遍历第二个文件中的所有整数,如果整数已经被映射到位图,那么它就是交集中的集合。
思路2:
- 创建2个大小相同的位图;
- 将第一个文件中的整数映射到位图1中;
- 将第二个文件中的整数映射到位图2中;
- 将位图 1 和位图 2 进行与操作,结果就是交集。
题目3
一个文件有 100 亿个整数,1G 内存,设计算法找到出现次数不超过 2 次的所有整数。
思路和题目1非常类似。无非就是将二进制序列增加到3:
- 00:出现0次;
- 01:出现1次;
- 10:出现2次;
- 11:出现3次及以上。
#include <iostream>
#include <vector>
#include <bitset>
using namespace std;
int main()
{
vector<int> v{1, 3, 5, 7, 9, 2, 4, 6, 8, 10, 1, 3, 5, 7, 9, 2};
bitset<4294967295>* bs1 = new bitset<4294967295>;
bitset<4294967295>* bs2 = new bitset<4294967295>;
for (auto e : v)
{
if (!bs1->test(e) && !bs2->test(e)) // 00->01
{
bs2->set(e);
}
else if (!bs1->test(e) && bs2->test(e)) // 01->10
{
bs1->set(e);
bs2->reset(e);
}
else if (bs1->test(e) && !bs2->test(e)) // 10->11
{
bs2->set(e);
}
else //
{
continue;
}
}
for (size_t i = 0; i < 4294967295; i++)
{
if (!bs1->test(i) && bs2->test(i)) // 01 or 10
cout << i << endl;
}
return 0;
}
输出
4
6
8
10
布隆过滤器的应用
布隆过滤器是位图的优化,它可以利用多个哈希函数字符串类型的元素处理。
问题1
近似算法要求没那么严格,允许误判的情况存在,所以可以考虑布隆过滤器。
- 先读取其中一个文件当中的query,将其全部映射到一个布隆过滤器。
- 然后读取另一个文件当中的query,依次判断每个 query 是否在布隆过滤器中,是则为交集,反之则否。
问题2
如何让布隆过滤器实现删除功能?
布隆过滤器一般不支持删除操作:
首先从原理上删除操作会直接影响哈希函数的结果,那么每一次删除都要重新把这个容器中的所有元素重新再映射一遍,影响了其他元素,降低效率。
其次布隆过滤器要删除一个元素,首先要保证它是真正存在这个集合中的,但是误判是无法避免的,所以删除有一定的风险。
要让布隆过滤器支持删除,必须要满足:
为每一个比特位增加一个引用计数,当在一个位置上增加一个元素,引用计数+1,反之-1,这样删除就不会改变布隆过滤器的长度,也就不会影响其他元素。但是这违背了布隆过滤器(位图)本身的应用场景:省空间+快速查询。
当使用Test接口得知元素可能存在于映射以后的布隆过滤器中,再进一步去原始文件验证这个元素是否存在于集合中。但这就像从内存中突然跳到磁盘文件中查找,文件IO和磁盘IO相对于内存而言是很慢的,所以还是降低了效率。
结合上面两点,再加上布隆过滤器本身的应用就是为了查询,而删除对它而言不痛不痒,因为位图这个容器是直接在内存中操作比特位的,即使有很多剩下的没用的元素,对计算机而言它也只是几个比特位,这是无关痛痒的。
哈希切割的应用
题目1
给两个文件,分别有 100 亿个 query,只有 1G 内存,如何找到两个文件的交集?给出精确算法。
精确算法不允许误判,考虑使用哈希切割,其实就是分治思想:将大问题转化为小问题。
假设每个 query 为 20 字节,100 亿个query就是200GB,由于只有 1GB 内存,考虑将一个文件切分成 400 个小文件。
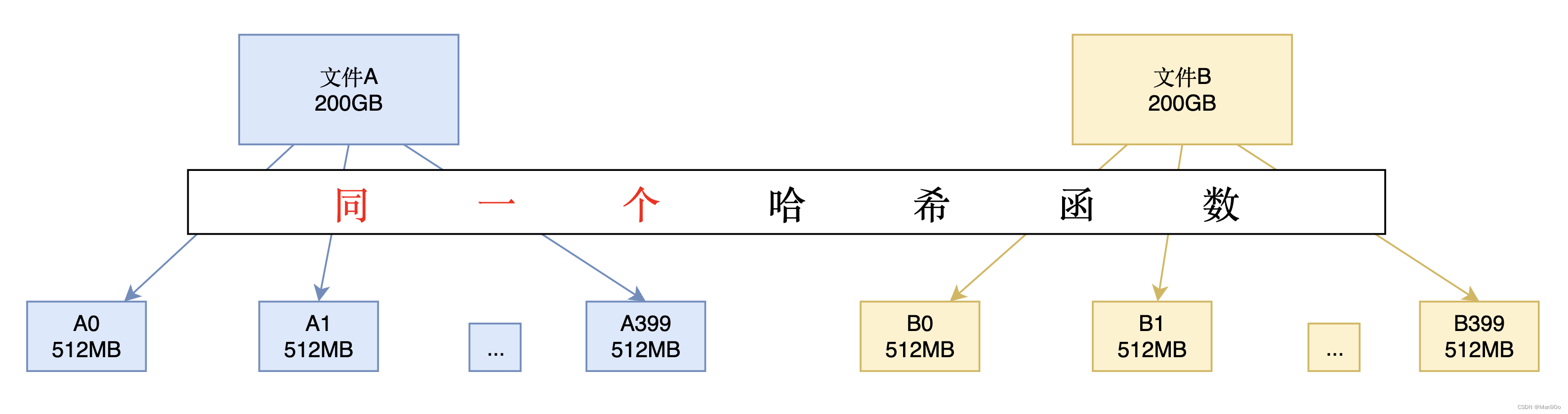
值得注意的是,必须使用同一个哈希函数对文件A和文件B的元素操作,才能实现“分而治之”的设想。原因是必须保证两个文件中每个小集合中每个元素的映射是正确的,才能保证两个文件的每个对应小集合是对应的。
-
切割以后的小文件大小是512MB,所以可以将一个个小文件加载到内存,用set容器存放,再遍历另一个小文件中的每个元素,判断这个文件中的元素是否存在于set容器中。在则是交集元素,反之则否。
-
哈希切割并不是平均切割,有可能切出来的小文件中有一些小文件的大小仍然大于 1GB,此时如果与之对应的另一个小文件可以加载到内存,则可以选择将另一个小文件中的元素加载到内存,因为目的是比较两文件的公有部分,所以只需要把其中一个小文件加载到内存。
-
但如果两个小文件的大小都大于 1GB,可以将这两个小文件再进行一次切割。
哈希切割的本质是:将小文件当做哈希桶,将大文件中的query通过哈希函数映射到这些哈希桶中,如果是相同的query,则会产生哈希冲突进入到同一个小文件中。
问题2
给一个超过 100G 大小的 log file,log 中存着 IP 地址,设计算法找到出现次数最多的 IP 地址?如何找到 top K 的 IP?如何直接用 Linux 系统命令实现?
哈希切割:
- 由于文件log file的大小超过100GB,考虑将文件log file切分成200个小文件。
- 使用相同的哈希函数切分文件,使得每个小文件能够以合适的大小(不影响效率)加载到内存中。同样的
- 遍历每个IP,然后将IP对应的哈希值写入它所在的小文件中。
查找出现次数最多的IP:
- 要找到出现次数最多的IP,依次将每个小文件加载到内存中, 然后用map容器统计出每个小文件中各个 IP 地址出现的次数,然后比对各个小文件中出现次数最多的 IP 地址,最后能得到出现次数最多的IP。
查找出现次数最多的前K个IP:
- TOP-K问题,用数据结构堆解决。用每个小文件中出现次数最多的IP建一个小堆,这个小堆的前K个IP就是出现次数最多的前K个IP。
在Linux中的操作:
用sort file_name | uniq -c | sort -nrk1,1 | head -K命令选取出现次数 top K 的 IP 地址。
- sort:对文件
file_name排序; - uniq:统计每个 IP 地址出现的次数;
- nrk1,1:再次使用
sort命令按照每个 IP 底层出现的次数进行反向排序; - head:选出出现次数前K个元素。