[开发测试]PAT A1046

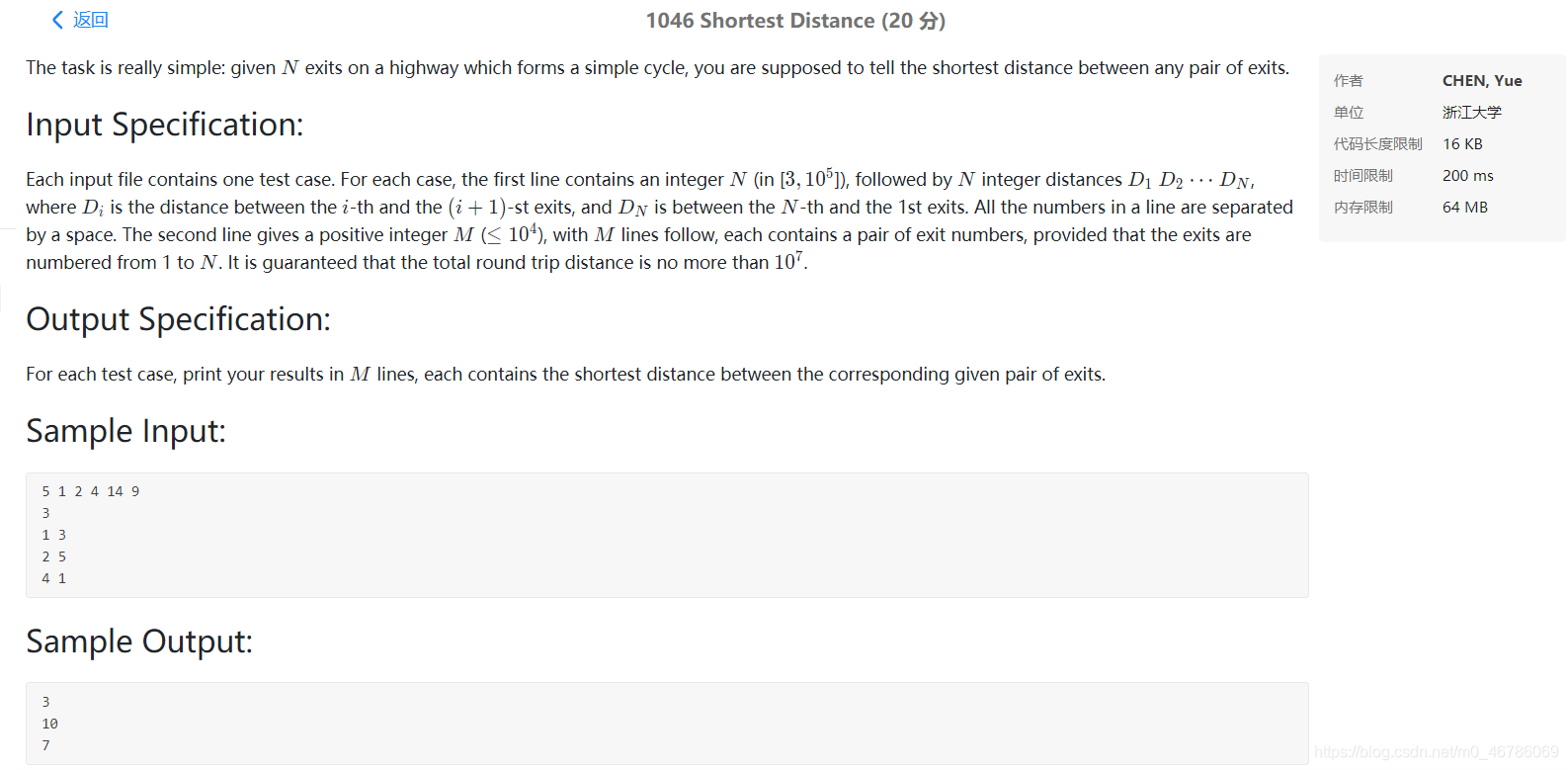
方法一：17分，最后一个测试用例超时。数组中存放相邻两点的距离，没有进行处理。每次循环操作都用不到之前的过程操作，进行了很多重复操作，所以会超时。

#include<cstdio>

const int MAXN = 100010;
int d[MAXN] = {0};

int main(){
	
	int n,sum = 0;	
	scanf("%d",&n);
	for(int i = 0; i < n; i++){
		scanf("%d",&d[i]);
		sum += d[i];	
	}
	int m,p,q;
	scanf("%d",&m);
	for(int i = 0; i < m; i++){
		scanf("%d%d",&p,&q);
		if(p > q){
			int t = p;
			p = q;
			q = t;
		}
		int r1 = 0,r2 = 0;
		for(int j = p - 1; j < q - 1; j++){
			r1 += d[j];
		}
		r2 = sum - r1;
		printf("%d\n",r1 > r2 ? r2 : r1);
	}
	return 0;
} 

方法二：满分通过，数组改为存放从第一个到当前点的距离之和，这样计算两点距离（不论多远），进行一次减法操作即可完成。类似动态规划的想法，把能重复用到的过程步骤结果保留下来。

#include<cstdio>

const int MAXN = 100010;
int d[MAXN] = {0};

int main(){
	
	int n,sum = 0;	
	scanf("%d",&n);
	d[0] = 0;
	for(int i = 1; i <= n; i++){
        int cur;
		scanf("%d",&cur);
		sum += cur;	
        d[i] = sum;
	}
	int m,p,q;
	scanf("%d",&m);
	for(int i = 0; i < m; i++){
		scanf("%d%d",&p,&q);
		if(p > q){
			int t = p;
			p = q;
			q = t;
		}
		int r1 = 0,r2 = 0;
        r1 = d[q - 1] - d[p - 1];
		r2 = sum - r1;
		printf("%d\n",r1 > r2 ? r2 : r1);
	}
	return 0;
}