最小生成树(Prim算法和Kruskal算法)
一、Prim算法
算法思路:
首先就是从图中的一个起点a开始,把a加入U集合,然后,寻找从与a有关联的边中,权重最小的那条边并且该边的终点b在顶点集合:(V-U)中,我们也把b加入到集合U中,并且输出边(a,b)的信息,这样我们的集合U就有:{a,b},然后,我们寻找与a关联和b关联的边中,权重最小的那条边并且该边的终点在集合:(V-U)中,我们把c加入到集合U中,并且输出对应的那条边的信息,这样我们的集合U就有:{a,b,c}这三个元素了,一次类推,直到所有顶点都加入到了集合U。
下面我们对下面这幅图求其最小生成树:

- 假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
- 然后,我们要从v1和v3作为起点的边中寻找权重最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4
- 然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2.
- 然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5
- 然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3
- 最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
二、Kruskal算法
算法思路:
(1)将图中的所有边都去掉。
(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环
(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
这里同样我们给出一个和Prim算法讲解中同样的例子,模拟克鲁斯卡算法生成最小生成树的详细的过程:
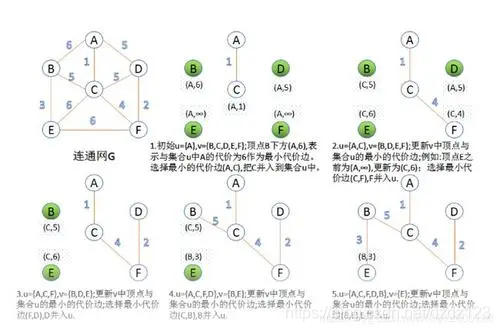
例题——1
HUD-1863
Problem Description
省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可)。经过调查评估,得到的统计表中列出了有可能建设公路的若干条道路的成本。现请你编写程序,计算出全省畅通需要的最低成本。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出评估的道路条数 N、村庄数目M ( < 100 );随后的 N
行对应村庄间道路的成本,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间道路的成本(也是正整数)。为简单起见,村庄从1到M编号。当N为0时,全部输入结束,相应的结果不要输出。
Output
对每个测试用例,在1行里输出全省畅通需要的最低成本。若统计数据不足以保证畅通,则输出“?”。
Sample Input
3 3
1 2 1
1 3 2
2 3 4
1 3
2 3 2
0 100
Sample Output
3
?
1—Prim算法
#include <queue>
#include <iostream>
#include <cstring>
#include <cmath>
#include <ctime>
#include <climits>
#include <vector>
#include <algorithm>
#include <map>
#include <cstdio>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
#define INF 0x3f3f3f3f
int N,M;
int x,y,z;
int Map[105][105],dist[105];
bool vis[105];
int sum;
void Prim(){
for(int i=1;i<=M;++i){//初始化dist[]数组
dist[i]=Map[1][i];//指示权值
}
memset(vis,0,sizeof(vis));//利用vis数组标记走过的点
vis[1]=1;
sum=0;
//核心
for(int i=1;i<=M;++i){
int minn=INF;
int cur=-1;
for(int j=2;j<=M;++j){
if(!vis[j]&&dist[j]<minn){//用于查找最小权值;
minn=dist[j];
cur=j;//权值指向的终点
}
}
if(cur==-1){//判断推出
break;
}
sum+=dist[cur];
vis[cur]=1;
for(int k=1;k<=M;++k){//更新dist数组指向的权值
if(!vis[k]&&dist[k]>Map[cur][k]){//更新最小值
dist[k]=Map[cur][k];
}
}
}
//判断各点是否连接
bool flag=true;
for(int i=1;i<=M;++i) if(!vis[i]){ flag=false; break;}
if(flag) printf("%d\n",sum);
else puts("?");
}
int main(){
while(~scanf("%d%d",&N,&M)&&N){
fill(Map[0],Map[0]+105*105,INF);
for(int i=1;i<=N;++i){
scanf("%d%d%d",&x,&y,&z);
if(Map[x][y]>z) Map[x][y]=Map[y][x]=z;
}
Prim();
}
return 0;
}
2——Kruskal算法
#include <queue>
#include <iostream>
#include <cstring>
#include <cmath>
#include <ctime>
#include <climits>
#include <vector>
#include <algorithm>
#include <map>
#include <cstdio>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const ULL maxn=2E5+10;
struct node
{
int x,y,z;
}edge[maxn];
bool cmp(node a,node b) {
return a.z < b.z;
}
int n,m;
ULL sum;
int vis[maxn];
void Init(){// 并查集 初始化函数
for(int i=0;i<=m;++i){ vis[i]=i;}
}
int Find(int n){// 并查集 查找函数
return n==vis[n] ? n : vis[n]=Find(vis[n]);
}
void Combine(int a,int b){// 并查集 合并函数
int x=Find(a);
int y=Find(b);
if(x==y) return;
vis[y]=x;
}
void Kruskal(){// 最小生成树 Kruskal 算法
Init();
sort(edge+1,edge+n+1,cmp);//长短排序
// 构建最小生成树
node point;
sum=0;
for(int i=1;i<=n;++i){
point=edge[i];
if(Find(point.x)!=Find(point.y)){//判断根节点是否相同
Combine(point.x,point.y);
sum+=edge[i].z;
}
}
}
int main(){
while(~scanf("%d%d",&n,&m)&&n&&m){
for(int i=1;i<=n;++i){ scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z);}
Kruskal();
//判断是否同一根节点
bool flag=true;
for(int i=2;i<=m;++i) {if(Find(1)!=Find(i)) {flag=false; break;}}
if(flag) printf("%lld\n",sum);
else puts("?");
}
return 0;
}
例题——2
HDU-1233
Problem Description
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 );随后的N(N-1)/2行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从1到N编号。
当N为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最小的公路总长度。
Sample Input
3
1 2 1
1 3 2
2 3 4
4
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
0
Sample Output
3
5
1——Prim算法
#include <queue>
#include <iostream>
#include <cstring>
#include <cmath>
#include <ctime>
#include <climits>
#include <vector>
#include <algorithm>
#include <map>
#include <bits/stdc++.h>
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int MAXN = 100;
const int INF = 0x3f3f3f3f;
bool vis[MAXN];
int dis[MAXN];
int G[MAXN][MAXN];
int n, m;
void init () {
memset(vis, 0, sizeof(vis));
fill(dis, dis + MAXN, INF);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
if(i == j) G[i][j] = 0;
else G[i][j] = INF;
}
}
}
void Prime () {
dis[1] = 0;
while (true) {
int k = -1, minn = INF;
for(int i = 1; i <= n; ++i) {
if( dis[i] < minn && !vis[i] ) {
k = i;
minn = dis[i];
}
}
if(k == -1) break;
vis[k] = 1;
for(int i = 1; i <= n; ++i) {
if (dis[i] > G[k][i] && !vis[i]) {
dis[i] = G[k][i];
}
}
}
int ans = 0;
for(int i = 1; i <= n; ++i) ans += dis[i];
cout << ans << endl;
}
int main(){
while (cin >> n && n) {
init();
m = n * (n - 1) / 2;
int x, y, z;
for(int i = 0; i < m; ++i) {
cin >> x >> y >> z;
if( G[x][y] > z) {
G[x][y] = z, G[y][x] = z;
}
}
Prime();
}
return 0;
}
2——Kruskal算法
#include <queue>
#include <iostream>
#include <cstring>
#include <cmath>
#include <ctime>
#include <climits>
#include <vector>
#include <algorithm>
#include <map>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const ULL maxn=2E5+10;
struct node
{
int x,y,z;
}edge[maxn];
bool cmp(node a,node b) {
return a.z < b.z;
}
int n,m;
ULL sum;
int vis[maxn];
int Find(int n){
return n==vis[n] ? n : vis[n]=next_get(vis[n]);
}
int Kruskal(){
sort(edge+1,edge+m+1,cmp);
sum=0;
for(int i=1;i<=m;++i){
int x=Find(edge[i].x);
int y=Find(edge[i].y);
if(x==y) continue;
vis[y]=x;
sum+=edge[i].z;
}
}
int main(){
while(~scanf("%d",&n)&&n){
m=n*(n-1)/2;
for(int i=1;i<=m;++i){ scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z);}
for(int i=0;i<=m;++i){ vis[i]=i;}
Kruskal();
int ans=0;
for(int i=1;i<=n;++i) {if(i==vis[i]) ans++;}
if(ans>1) puts("impossible\n");
else printf("%lld\n",sum);
}
return 0;
}