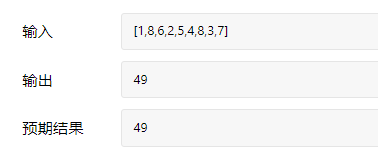
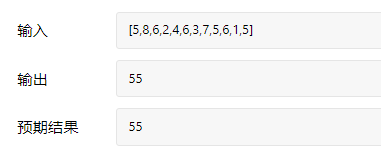
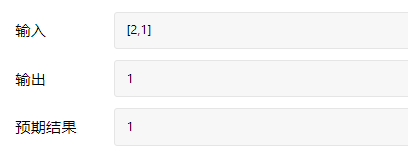
题目要求

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

思路

可以定义两个变量，一个代表数组的第0位，一个代表数组的最后一位，用数组height[1,8,6,2,5,4,8,3,7]来举例
定义i表示height[0]，定义j表示height[height.length-1]
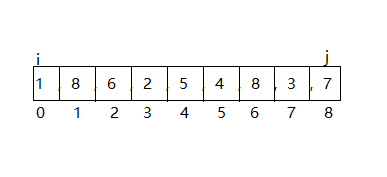
在这里插入图片描述
取出这两个数中最小的数，乘这两个数之间的距离，可以得到一个结果
1x（8-0） = 8
将这个结果用tmp保存下来，移动i和j中较小的一方

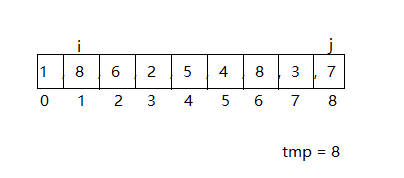
重复上面的步骤，可以得出一个结果
7x（8-1） = 49
与tmp进行比较，如果大于tmp就刷新tmp的值，移动i和j中较小的一方
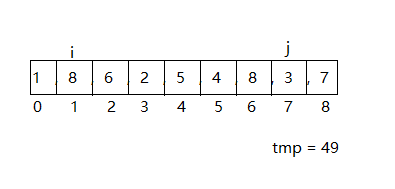
在这里插入图片描述
以此类推，最后可以得出一个最大值

代码实现

class Solution {
    public int maxArea(int[] height) {
        int tmp = 0;
        int n = 0;
        int i = 0;
        int j = height.length-1;
        while(i<j){//i的值如果大于j没有意义
            if(height[i]<=height[j]){//比较两个数的大小
                n = height[i]*(j-i);
                if(n>tmp){
                    tmp = n;//刷新tmp的值
                }
                i++;
            }else{
                n = height[j]*(j-i);
                if(n>tmp){
                    tmp = n;
                }
                j--;
            }
        }
        return tmp;
    }
}