[开发测试]有向图D和E

题目大意
　　对于一个有 n 个节点的有向图 D，可以构造这样一个图 E，即 D 的每条边对应 E 的一个结点（例如，若 D 有一条边（ u，v），则 E 有个结点的名字叫 uv），对于 D 的两条边 uv 和 vw，E 中的两个结点 uv 和 vw 之间连一条有向边。E 中不包含其他边。

输入：第一行包含测试用例数N（N<200）,在每个测试用例的前两行包含一个 m(0 ≤ m ≤ 300) 和 k，表示图 E中的节点数和边数 ，判断是否存在对应的图 D。E 中各个结点的编号为 0~m-1。
　　输出：对于每个测试用例，都输出一个Case#t，其中t表示测试用例编号，然后是Yes或者No，用于判断E是否是一个有向图D对应生成。
　　输入样例：
　　4
　　2
　　1
　　0 1
　　5
　　0
　　4
　　3
　　0 1
　　2 1
　　2 3
　　3
　　9
　　0 1
　　0 2
　　1 2
　　1 0
　　2 0
　　2 1
　　0 0
　　1 1
　　2 2
　　输出样例：
　　Case#1：Yes
　　Case#2：Yes
　　Case#3：No
　　Case#4：Yes
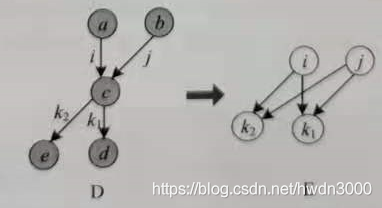
题解：本题实际上就是把D中的边缩成点，D中的一条边对应E中的一个节点，如果在D中存在边i（u，v）和j（v，w），则E将具有从节点i到节点j的边。

如果在D中边i和边j有公共端点，则i连接的边，j也一定连接，不存在i连接的边而j没连接的情况。
那么在E中，节点i和节点j有公共邻接点，则i邻接的节点，j也一定邻接。
如下图中：

算法设计：
（1）：用邻接矩阵存储E
（2）：判断在E中是否存在节点i和节点j有公共邻节点但是对i邻接的节点而对j不邻接的情况。有这种情况就找不出E对应的D，就输出No

代码：

#include<bits/stdc++.h>
#define REP(i,b,e) for(int i=(b);i<(e);i++)
using namespace std;
const int maxn=300+5;
int g[maxn][maxn],n,m;

bool solve(){
	REP(i,0,n)
		REP(j,0,n){
			bool flag1=false,flag2=false;
			REP(k,0,n){
				if(g[i][k]&&g[j][k])
					flag1=true;
				if(g[i][k]^g[j][k])
					flag2=true;
			}
			if(flag1&&flag2)
				return false;
		}
	return true;
}

int main(){
	int T,cnt=0,x,y;
	cin>>T;
	while(T--){
		memset(g,0,sizeof(g));//初始化邻接矩阵 
		cin>>n>>m;
		REP(i,0,m){
			cin>>x>>y;
			g[x][y]=1;
		}
		if(solve())
			cout<<"Case #"<<++cnt<<": Yes"<<endl;
		else
			cout<<"Case #"<<++cnt<<": No"<<endl;
	}
	return 0;
}