Parsa’s Humongous Tree
Description
Parsa has a humongous tree on n vertices.
On each vertex v he has written two integers lv and rv.
To make Parsa’s tree look even more majestic, Nima wants to assign a number av (lv≤av≤rv) to each vertex v such that the beauty of Parsa’s tree is maximized.
Nima’s sense of the beauty is rather bizarre. He defines the beauty of the tree as the sum of |au?av| over all edges (u,v) of the tree.
Since Parsa’s tree is too large, Nima can’t maximize its beauty on his own. Your task is to find the maximum possible beauty for Parsa’s tree.
Input
The first line contains an integer t (1≤t≤250) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n (2≤n≤105) — the number of vertices in Parsa’s tree.
The i-th of the following n lines contains two integers li and ri (1≤li≤ri≤109).
Each of the next n?1 lines contains two integers u and v (1≤u,v≤n,u≠v) meaning that there is an edge between the vertices u and v in Parsa’s tree.
It is guaranteed that the given graph is a tree.
It is guaranteed that the sum of n over all test cases doesn’t exceed 2?105.
Output
For each test case print the maximum possible beauty for Parsa’s tree.
Example
input
3
2
1 6
3 8
1 2
3
1 3
4 6
7 9
1 2
2 3
6
3 14
12 20
12 19
2 12
10 17
3 17
3 2
6 5
1 5
2 6
4 6
output
7
8
62
Note
The trees in the example:
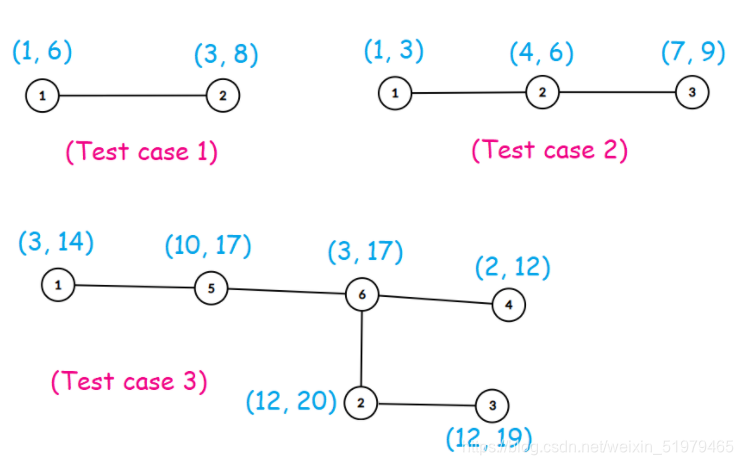
In the first test case, one possible assignment is a={1,8} which results in |1?8|=7.
In the second test case, one of the possible assignments is a={1,5,9} which results in a beauty of |1?5|+|5?9|=8
大意
从前有一棵 n 个点的大树,每个顶点 v 上有两个数lv,rv
为了使这棵树看起来更加雄伟,小羊驼 想为每个顶点 v 分配一个数字 av (lv≤av≤rv),从而最大化 这棵树的价值。
小羊驼将树的价值定义为:对于在树的所有边 (u,v) 其 |au?av| 的总和。 由于这棵树太大了,小羊驼算不出他的最大价值是多少,你的任务是帮助小羊驼算出这棵树的最大价值
Input
第一行包含一个整数 t (1≤t≤250)——测试用例的数量。 测试用例的描述如下。 每个测试用例的第一行包含一个整数 n (2≤n≤105)——Parsa 树中的顶点数。 以下n行的第i行包含两个整数li和ri(1≤li≤ri≤109)。 接下来的 n-1 行中的每一行都包含两个整数 u 和 v (1≤u,v≤n,u≠v),这意味着 Parsa 树中的顶点 u 和 v 之间有一条边。 保证给定的图是一棵树。 保证所有测试用例的 n 总和不超过 2?105。
Output
对于每个测试用例,打印该树的最大可能价值。
思路
对于每个节点,这个节点的权值只在一个区间内取值,假设他取到一个点x,然后与他相邻的节点中取得的值比x大的有a个,比x小的有b个,因为其他的点已经确定了,咱们不妨设a>=b,那么把x往左边界移动一定会使这个点对与他相邻的边的贡献增大,反之就往右边界移动,那么就可以证明这个点选数不是在左边界就是在右边界,咱们可以开两个数组一个记录选左边界时候的子树的最大值,一个记录选右边界时候的子树的最大值,最后取一个max就是答案,下面请看代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 100010,M = N*2;
typedef long long LL;
LL f1[N],f2[N],l[N],r[N];
int h[N],e[M],ne[M],idx,n;
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u,int fa){
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
if(j == fa) continue;
dfs(j,u);
f1[u] += 1ll*max(f1[j] + abs(l[u]-l[j]),f2[j] + abs(l[u]-r[j]));//选左边界
f2[u] += 1ll*max(f1[j] + abs(r[u]-l[j]),f2[j] + abs(r[u]-r[j]));//选右边界
}
}
int main(){
int t;
scanf("%d",&t);
while(t--){
memset(h,-1,sizeof h);
idx=0;
scanf("%d",&n);
for(int i=0;i<=n;i++) f1[i] = f2[i] = 0;
for(int i=1;i<=n;i++) scanf("%lld%lld",&l[i],&r[i]);
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
dfs(1,0);
printf("%lld\n",max(f1[1],f2[1]));
}
return 0;
}