[开发测试]数据分析中最常听到的A/B测试究竟如何理解？附天池项目实战演练

今天分享一下一个利用A/B测试解决问题的项目，本文会尽可能详细的将我所理解的A/B测试应用到项目当中，希望对大家有所帮助。

那在开始之前我会在重新介绍一下什么是A/B测试？

一、A/B测试

A/B测试类似于以前的对比实验，是让组成成分相同（相似）的群组在同一时间维度下去随机的使用一个方案（方案A、或者B、C…），收集各组用户体验数据和业务数据，最后分析出哪个方案最好。

实现步骤

1. 现状分析：分析业务数据，确定当前最关键的改进点。
2. 假设建立：根据现状分析作出优化改进的假设，提出优化建议。
3. 设定目标：设置主要目标，用来衡量各优化版本的优劣；设置辅助目标，用来评估优化版本对其他方面的影响。
4. 设计开发：制作若干个优化版本的设计原型。
5. 确定分流方案：使用各类A/B测试平台分配流量。初始阶段，优化方案的流量设置可以较小，根据情况逐渐增加流量。注意分流时要尽可能做到没有区别。
6. 采集数据：通过各大平台自身的数据收集系统自动采集数据。
7. 分析A/B测试结果：统计显著性达到95%（一般设为95%）或以上并且维持一段时间，实验可以结束；如果在95%以下，则可能需要延长测试时间；如果很长时间统计显著性不能达到95%甚至90%，则需要决定是否中止试验或重新设计方案。

假设检验

要想充分搞懂A/B测试，必须理解它的原理——假设检验。
在一个设计适当的 A/B 测试中，处理 A 和处理 B 之间任何可观测到的差异，必定是由下面两个因素之一所导致的。

• 分配对象中的随机可能性
• 处理 A 和处理 B 之间的真实差异

假设检验是对 A/B 测试（或任何随机实验）的进一步分析，意在评估随机性是否可以合理地解释 A 组和 B 组之间观测到的差异。

这里需要介绍一下几个专业术语：

• 零假设：完全归咎于偶然性的假设，即各个处理是等同的，并且组间差异完全是由偶然性所导致的。
  事实上，我们希望能证明零假设是错误的，并证明 A 和 B 结果之间的差异要比偶然性可能导致的差异更大。
• 备择假设：与零假设相反，即实验者希望证实的假设。
• 单向检验：在假设检验中，只从一个方向上计数偶然性结果。简单来讲就是最终只需判断大于或者只需判断小于。
• 双向检验：在假设检验中，从正反两个方向上计数偶然性结果。

假设检验的基本思想是“小概率事件”原理，其统计推断方法是带有某种概率性质的反证法。小概率思想是指小概率事件在一次试验中基本上不会发生。反证法思想是先提出检验假设，再用适当的统计方法，利用小概率原理，确定假设是否成立。对于不同的问题，检验的显著性水平α不一定相同，一般认为，事件发生的概率小于0.1、0.05或0.01等，即“小概率事件”。

接下来介绍假设检验的基本步骤：

1. 提出零假设和备择假设；
2. 根据备择假设确定检验方向；
   简单来说含有不等号的是双向检验，反之则是单向检验，其中<为左，>为右；
3. 选定统计方法。根据资料的类型和特点，可分别选用Z检验、T检验，秩和检验和卡方检验等；
4. 选定显著性水平α。但记住判断结论时不能绝对化，应注意无论接受或拒绝检验假设，都有判断错误的可能性。

检验方法

u检验和t检验

t检验是用t分布理论来推断差异发生的概率，从而判定两总体均数的差异是否有统计学意义，主要用于样本含量较小(如n<60)，总体标准差σ未知，呈正态分布的计量资料。若样本含量较大(如n>60)，或样本含量虽小，但总体标准差σ已知，则可采用u检验(亦称：z检验)。但在统计软件中，无论样本量大小，均采用t检验进行统计分析 。

t检验和u检验的适用条件：①样本来自正态总体或近似正态总体；②两样本总体方差相等，即具有方差齐性。在实际应用时，如与上述条件略有偏离，对结果亦不会有太大影响；③两组样本应相互独立。根据比较对象的不同，t检验又分为单样本t检验、配对t检验和两独立样本t检验。

F检验

采用F检验检验方差齐性，要求样本均来自正态分布的总体。检验统计量F等于两样本的较大方差 比较小方差 ，其检验统计量公式为：
$$F=\frac{S_2^1}{S_2^2},v_1=n_1?1,v_2=n_2?1$$数理统计理论证明：当$H_0（{\sigma }_1^2={\sigma }_2^2）$成立时，$\frac{S_2^1}{S_2^2}$服从F分布。F分布曲线的形状由两个参数$v_1=n_1?1和v_2=n_2?1$决定，F的取值范围为0~∞。

统计学家为应用的方便编制了的F分布临界值表，求得F值后，查F界值表得P值（F值愈大，P值愈小），然后按所取的α水准做出推断结论。

由于第一个样本的方差既可能大于第二个样本的方差，也可能小于第二个样本的方差，故两样本方差比较的F检验是双侧检验。

二、项目实战

项目来源：
https://tianchi.aliyun.com/dataset/dataDetail?dataId=50893

数据介绍：
从支付宝的两个营销活动中收集的真实数据集。该数据集包含支付宝中的两个商业定位活动日志。由于隐私问题，数据被采样和脱敏。虽然该数据集的统计结果与支付宝的实际规模有偏差，但不影响解决方案的适用性。

主要提供了三个数据集：

• emb_tb_2.csv: 用户特征数据集。
• effect_tb.csv: 广告点击情况数据集。
• seed_cand_tb.csv: 用户类型数据集。

本分析报告的主要使用广告点击情况数据，涉及字段如下：

• dmp_id：营销策略编号（这里我们这么设置1为对照组，2为营销策略一，3为营销策略二）。
• user_id：支付宝用户ID。
• label：用户当天是否点击活动广告（0：未点击，1：点击）。

接下来正式开始实战。

1 数据预处理

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

data = pd.read_csv('effect_tb.csv',header = None)
data.columns = ['dt','user_id','label','dmp_id']  # 文件中没有字段名
# 日志天数属性用不上，删除该列
data = data.drop(columns='dt')
data

data.info(null_counts = True)

查看数据统计情况，主要是看dmp_id。

data.describe()

接下来查看数据重复情况。

data[data.duplicated(keep = False)]

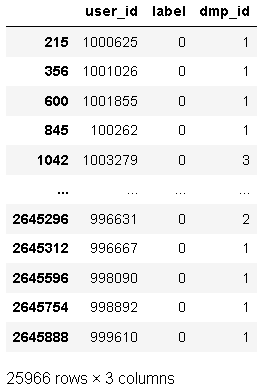
存在重复项，需要进行去重。

data = data.drop_duplicates()

# 检查是否还有重复项
data[data.duplicated(keep = False)]

从先前操作已知数据类型正常，接下来利用透视表来看各属性是否存在不合理情况。

data.pivot_table(index = 'dmp_id',columns = 'label',values = 'user_id',aggfunc = 'count') 

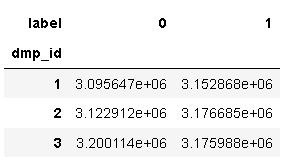
从以上看出属性字段无异常取值，无需进行处理。

2 样本容量检验

在进行A/B测试前，需检查样本容量是否满足试验所需最小值。

这里需要借助样本量计算工具：https://www.evanmiller.org/ab-testing/sample-size.html

首先需要设定点击率基准线以及最小提升比例，我们将对照组的点击率设为基准线。

data[data["dmp_id"] == 1]["label"].mean()

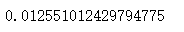
对照组的点击率为1.26%，假设我们希望新的营销策略能够让广告点击率至少提升一个百分点，则算得所需最小样本量为2167。

data["dmp_id"].value_counts()

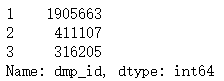
可得411107和316205远大于2167，满足最小样本量需求。

3 假设检验

我们先查看一下这三种营销策略的点击率情况。

print("对照组： " ,data[data["dmp_id"] == 1]["label"].describe())
print("策略一： " ,data[data["dmp_id"] == 2]["label"].describe())
print("策略二： " ,data[data["dmp_id"] == 3]["label"].describe())

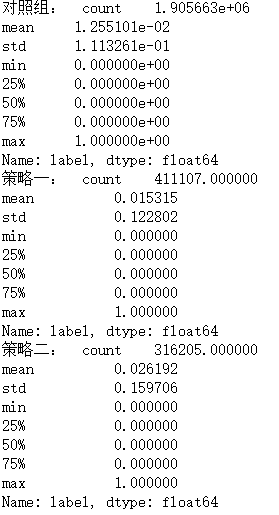
可以看到策略一和策略二相比对照组在点击率上都有不同程度的提升。

其中策略一提升0.2个百分点，策略二提升1.3个百分点，只有策略二满足了前面我们对点击率提升最小值的要求。

接下来需要进行假设检验，看策略二点击率的提升是否显著。

3.1 提出零假设和备择假设

设对照组点击率为$p_1$，策略二点击率为$p_2$，则：

• 零假设$H_0$：$p_1$>=$p_2$，即$p_1$-$p_2$>=0；
• 备择假设$H_1$：$p_1$<$p_2$，即$p_1$-$p_2$<0。

3.2 确定检验方向

由备择假设可以看出，检验方向为单项检验（左）。

3.3 选定统计方法

由于样本较大，故采用Z检验。此时检验统计量的公式如下：$$z=\frac{p_1?p_2}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})\times p_c\times (1?p_c)}}$$其中$p_c$为总和点击率。

3.3.1 方法一：公式计算

# 用户数
n1 = len(data[data.dmp_id == 1])  # 对照组
n2 = len(data[data.dmp_id == 3])  # 策略二

# 点击数
c1 = len(data[data.dmp_id ==1][data.label == 1])
c2 = len(data[data.dmp_id ==3][data.label == 1])

# 计算点击率
p1 = c1 / n1
p2 = c2 / n2

# 总和点击率（点击率的联合估计）
pc = (c1 + c2) / (n1 + n2)

print("总和点击率pc：", pc)

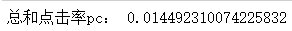
# 计算检验统计量z
z = (p1 - p2) / np.sqrt(pc * (1 - pc)*(1/n1 + 1/n2))

print("检验统计量z：", z)

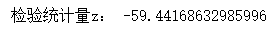
这里我去 $\alpha$为0.05，此时我们利用python提供的scipy模块，查询$\alpha =0.5$时对应的z分位数。

from scipy.stats import norm
z_alpha = norm.ppf(0.05)
# 若为双侧，则norm.ppf(0.05/2)
z_alpha

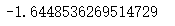
$z_{\alpha }=?1.64$， 检验统计量z = -59.44，该检验为左侧单尾检验，拒绝域为{z＜$z_{\alpha }$}，z=-59.44落在拒绝域。

所以我们可以得出结论：在显著性水平为0.05时，拒绝原假设，策略二点击率的提升在统计上是显著的。

假设检验并不能真正的衡量差异的大小，它只能判断差异是否比随机造成的更大。因此，我们在报告假设检验结果的同时，应给出效应的大小。对比平均值时，衡量效应大小的常见标准之一是Cohen’d，中文一般翻译作科恩d值：$$d=\frac{样{本}_1平均值?样{本}_2平均值}{标准差}$$
这里的标准差，由于是双独立样本的，需要用合并标准差（pooled standard deviations）代替。也就是以合并标准差为单位，计算两个样本平均值之间相差多少。双独立样本的合并标准差可以如下计算：$$s=\frac{((n_1?1)\times s_1^2+(n_2?1)\times s_2^2)}{n_1+n_2?2}$$

其中s是合并标准差，n1和n2是第一个样本和第二个样本的大小，s1和s2是第一个和第二个样本的标准差。减法是对自由度数量的调整。

# 合并标准差
std1 = data[data.dmp_id ==1].label.std()
std2 = data[data.dmp_id ==3].label.std()
s = np.sqrt(((n1 - 1)* std1**2 + (n2 - 1)* std2**2 ) / (n1 + n2 - 2))
# 效应量Cohen's d
d = (p1 - p2) / s
print('Cohen\'s d为：', d)

一般上baiCohen’s d取值0.2-0.5为小效应，0.5-0.8中等效应，0.8以上为大效应。

3.3.2 方法二：Python函数计算

import statsmodels.stats.proportion as sp
# alternative='smaller'代表左尾
z_score, p = sp.proportions_ztest([c1, c2], [n1,n2], alternative = "smaller")
print("检验统计量z：",z_score,"，p值：", p)

用p值判断与用检验统计量z判断是等效的，这里p值为0，同样也拒绝零假设。

至此，我们可以给出报告：

• 对照组的点击率为：0.0126，标准差为：0.11
• 策略二的点击率为：0.0262，标准差为：0.16
• 独立样本z=-59.44，p=0，单尾检验（左），拒绝零假设。
• 效应量Cohen’s d= -0.11，较小。

根据前面案例，我们用的是两个比率的z检验函数proportion.proportions_ztest，输入的是两组各自的总数和点击率；如果是一般性的z检验，可以用weightstats.ztest函数，直接输入两组的具体数值，可参考https://www.statsmodels.org/stable/generated/statsmodels.stats.weightstats.ztest.html

import statsmodels.stats.weightstats as sw
z_score1, p_value1 = sw.ztest(data[data.dmp_id ==1].label, data[data.dmp_id ==3].label, alternative='smaller')
print('检验统计量z:', z_score1, '，p值:', p_value1)

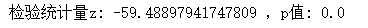
可以看到计算结果很接近，但是有点差异。因为非比率的z检验是不计算联合估计的。

作为补充，我们再检验下策略一的点击率提升是否显著。

z_score, p = sp.proportions_ztest([c1, len(data[data.dmp_id ==2][data.label == 1])],[n1, len(data[data.dmp_id ==2])], alternative = "smaller")
print('检验统计量Z:',z_score,',p值：',p)

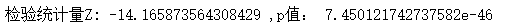
p值约为 7.450121742737582e-46，p<α,但是因为前面我们设置了对点击率提升的最小要求（1%），这里仍然只选择第二组策略进行推广。

3.3.3 方法三：蒙特卡洛法模拟

蒙特卡洛法其实就是模拟法，用计算机模拟多次抽样，获得分布。

在零假设成立（p1>=p2）的前提下， p1=p2 为临界情况（即零假设中最接近备择假设的情况）。如果连相等的情况都能拒绝，那么零假设的剩下部分（ p1>p2）就更能够拒绝了。

定义effect_tb.csv中样本的总点击率为 p_all：

p_all = data.label.mean()
print('p_all:', p_all)

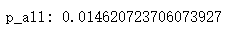
我们进行一次模拟，以 p_all 为对照组和策略二共同的点击率，即取p_old=p_new=p_all，分别进行n_old次和n_new次二点分布的抽样，使模拟的样本大小同effect_tb.csv中的样本大小相同：

choice1 = np.random.choice(2, size=n1, p=[1-p_all, p_all])
choice2 = np.random.choice(2, size=n2, p=[1-p_all, p_all])
diff = choice1.mean() - choice2.mean()
print('对照组结果：', choice1, '，策略二结果：', choice2, '，模拟的转化率差值：', diff)

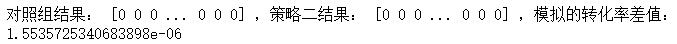
因为是随机抽样，所以每次模拟的点击率差值也是不同的，多运行几次就会发现，我们模拟出的结果很难比effect_tb.csv中样本的点击率差值更小，这说明了什么？

# 计算effect_tb.csv样本的点击率差值
data_diff = data[data["dmp_id"] == 1]["label"].mean()-data[data["dmp_id"] == 3]["label"].mean()
print('effect_tb.csv样本的点击率差值:', data_diff)

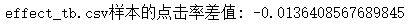
按照如上方式进行多次模拟，这里我们进行10000次，并计算出每个样本得到的策略点击率差值，将其存储在diffs中：

diffs=[]
for i in range(10000):
    p2_diff = np.random.choice(2,size=n2,p=[1-p_all,p_all]).mean()
    p1_diff = np.random.choice(2,size=n1,p=[1-p_all,p_all]).mean()
    diffs.append(p1_diff - p2_diff)

实际上每次模拟都得到了一个大小为316205的样本，此处得到了10000个样本。在图上将模拟得到的diffs绘制为直方图，将effect_tb.csv中样本的点击率差值绘制为竖线：

diffs = np.array(diffs)
plt.hist(diffs)
plt.axvline(data_diff)

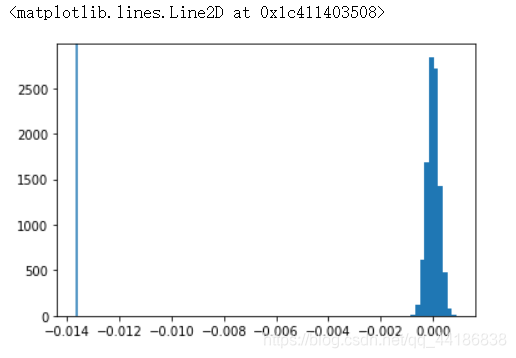
在diffs列表的数值中，有多大比例小于effect_tb.csv中观察到的点击率率差值？

(diffs < data_diff).mean()

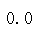
本次方法得到的答案是0,和方法二中的P值接近（一样）。

上图的含义是，在p_old=p_new时，进行10000次模拟得到的差值中，0%的可能比effect_tb.csv中的差值更极端，说明effect_tb.csv在p_old=p_new的前提是很小概率（这次是0概率）事件。反过来说，我们只做了一次A/B测试就得到了零假设中的极端情况，则零假设很有可能是不成立的。

• 现在图中的直方图是，若对照组和策略二的点击率相等，随机10000次，两者的差值的分布。
• 因为次数够多，根据大数定律，近似于真实的分布。
• 越靠近中间的部分，说明该数值出现的次数越多，越靠近两侧，说明该数值出现的越少，也可以说情况就越极端。
• 竖线是样本effect_tb.csv的差值所在位置，它落在了很左侧，体现在竖线左侧的面积（这次为0）很小。
• 竖线左侧的面积占比，即发生“竖线及竖线左侧极端情况”（diff<=-0.014）的可能性。
• 也就是说，effect_tb.csv这个样本，在对照组和策略二点击率相等的情况下，有可能出现，但出现的可能性很小（这次为0）。
• 所以反推出，对照组和策略二的点击率很有可能不相等。

思考：

若diffs的分布就是标准正态（这里只是近似），则竖线左侧的面积占比其实就是p值（左侧or右侧or双侧要根据备择假设给定的方向），那p值到底要多小才算真的小？

这需要我们自己给定一个标准，这个标准其实就是 α，是犯第一类错误的上界，常见的取值有0.1、0.05、0.01。

• 所谓第一类错误，即拒真错误，也就是零假设为真，我们却拒绝了。所以要取定一个 α ，并规定当p值小于 α 时，认为原假设在该显著性水平下被拒绝。
• 还有第二类错误——取伪，即零假设明明是错的，但是我们保留了零假设。拒真的可能性越小，则取伪的可能性越大。所以不能一味地取极小的α 。

4 结论

通过三种方法的计算得出，在两种营销策略中，策略二对广告点击率有显著提升效果，且相较于对照组点击率提升了近一倍，因而在两组营销策略中应选择第二组进行推广。

参考鸣谢：
https://baike.baidu.com/item/AB测试/9231223?fr=aladdin
https://baike.baidu.com/item/假设检验
https://zhuanlan.zhihu.com/p/68019926
《面对数据科学家的实用统计学》