A:Mocha and Math
给定一个长度为n的序列,选择一个区间 [L, R] ,对于所有的值i(0≤i≤r-l),同时用aL + i &
aR - i 替换aL + i 。这个操作可以进行任意次。求序列最大值的最小值。
一个简单的例子 2 3 7 9 ,他们的二进制表示为
0010
0011
0111
1011
由位与的性质易知,只要某个数位上存在0 ,它可以通过操作扩散到每一个值,即答案中该数位为0。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
#define all(x) x.begin(), x.end()
#define maxi(x) max_element(x.begin(), x.end()) - x.begin()
#define mini(x) min_element(x.begin(), x.end()) - x.begin()
void solve()
{
bool a[32];
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
ll x;
cin >> x;
for (i = 0; i <= 31; i++)
{
if ((x >> i) == 0)
a[i] = true;
}
}
ll p = 1, ans = 0;
for (int i = 0; i <= 32; i++)
{
if (!a[i])
p *= 2;
}
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
B:Mocha and Red and Blue
有n个方块排成一排,每个方块都可以涂成红色或蓝色。
在这些方格中,有些方格已经被涂过了,其他的方格则是空白。你可以决定在每个空白方格上涂抹哪种颜色。
一些相邻的方格可能具有相同的颜色,这是不完美的。我们将不完美度定义为相邻方格中拥有相同颜色的对数。你的目标是将不完美度降到最低,并打印出涂色后的方格颜色。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
#define all(x) x.begin(), x.end()
#define maxi(x) max_element(x.begin(), x.end()) - x.begin()
#define mini(x) min_element(x.begin(), x.end()) - x.begin()
const int maxn = 200;
void solve()
{
int n;
cin >> n;
string s;
cin >> s;
int f1 = 0;
int ans[maxn];
memset(ans, 0, sizeof ans);
int flag;
for (int i = 0; i < s.size(); i++)
if (s[i] == 'B')
{
f1 = i;
flag = 2;
break;
}
else if (s[i] == 'R')
{
f1 = i;
flag = 1;
break;
}
for (int i = f1 - 1; i >= 0; i--)
{
ans[i] = flag;
if (flag == 1)
flag = 2;
else
flag = 1;
}
for (int i = f1; i < s.size(); i++)
{
if (s[i] == 'B')
{
ans[i] = 1;
flag = 2;
}
else if (s[i] == 'R')
{
ans[i] = 2;
flag = 1;
}
else
{
ans[i] = flag;
if (flag == 1)
flag = 2;
else
flag = 1;
}
}
for(int i=0;i<s.size();i++)
if(ans[i]==1)
cout<<"B";
else
cout<<"R";
cout<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
C:Mocha and Hiking
摩卡居住的城市叫芷江。这个城市有n+1个村庄和2n-1条定向路。
有两种道路。
n-1条道路是从i村到i+1村,1≤i≤n-1。
n条道路可以用一个序列a1,…,an来描述。如果ai=0,这些道路中的第i条就是从村庄i到村庄n+1,否则就是从村庄n+1到村庄i,1≤i≤n。
摩卡计划这个周末和塔基一起去徒步旅行。为了避免旅行的枯燥,他们计划每一个村庄都正好经过一次。他们可以在任何村庄开始和结束。你能帮助他们制定一个计划吗?
容易得知只存在三种情况。
- 如果村庄1为n+1的出路,则答案为 n+1 1 2 3 … n
- 否则找到一个01串,0进1出。例如 0 0 1 0 ,则答案可以为 1 2 n+1 3 4
- 否则,如果全为0,则在村庄n进入村庄n+1
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
#define all(x) x.begin(), x.end()
#define maxi(x) max_element(x.begin(), x.end()) - x.begin()
#define mini(x) min_element(x.begin(), x.end()) - x.begin()
const int maxn = 1e4 + 10;
void solve()
{
int n;
cin >> n;
int x1 = -1;
int flag1 = 0;
int a[maxn];
for (int i = 1; i <= n; i++)
cin >> a[i];
if (a[1] == 1)
{
cout << n + 1 << " ";
for (int i = 1; i <= n; i++)
cout << i << " ";
cout << endl;
return;
}
int flag2 = 0;
for (int i = 1; i <= n; i++)
{
if (a[i] == 0)
flag2 = 1;
if (a[i] == 1 && flag2 == 1)
{
for (int j = 1; j <= i - 1; j++)
cout << j << " ";
cout << n + 1 << " ";
for (int j = i; j <= n; j++)
cout << j << " ";
cout << endl;
return;
}
}
for (int i = 1; i <= n + 1; i++)
cout << i << " ";
cout << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
D1 & 2. Mocha and Diana (Easy & Hard Version)
摩卡和戴安娜是芷江的朋友,他们都有一个节点编号从1到n的森林,他们想给自己的森林添加边,这样。
添加边后,他们的图都还是森林。
他们添加的边都是一样的。也就是说,如果一条边(u,v)被添加到摩卡的森林中,那么一条边(u,v)被添加到戴安娜的森林中,反之亦然。
摩卡和戴安娜想知道他们能增加的最大边数,以及要增加哪些边。
简单思考就能发现这是个并查集问题。
对于D1,数据范围较小,直接n2枚举每一条边判断即可。
对于D2,可以贪心地去找边。
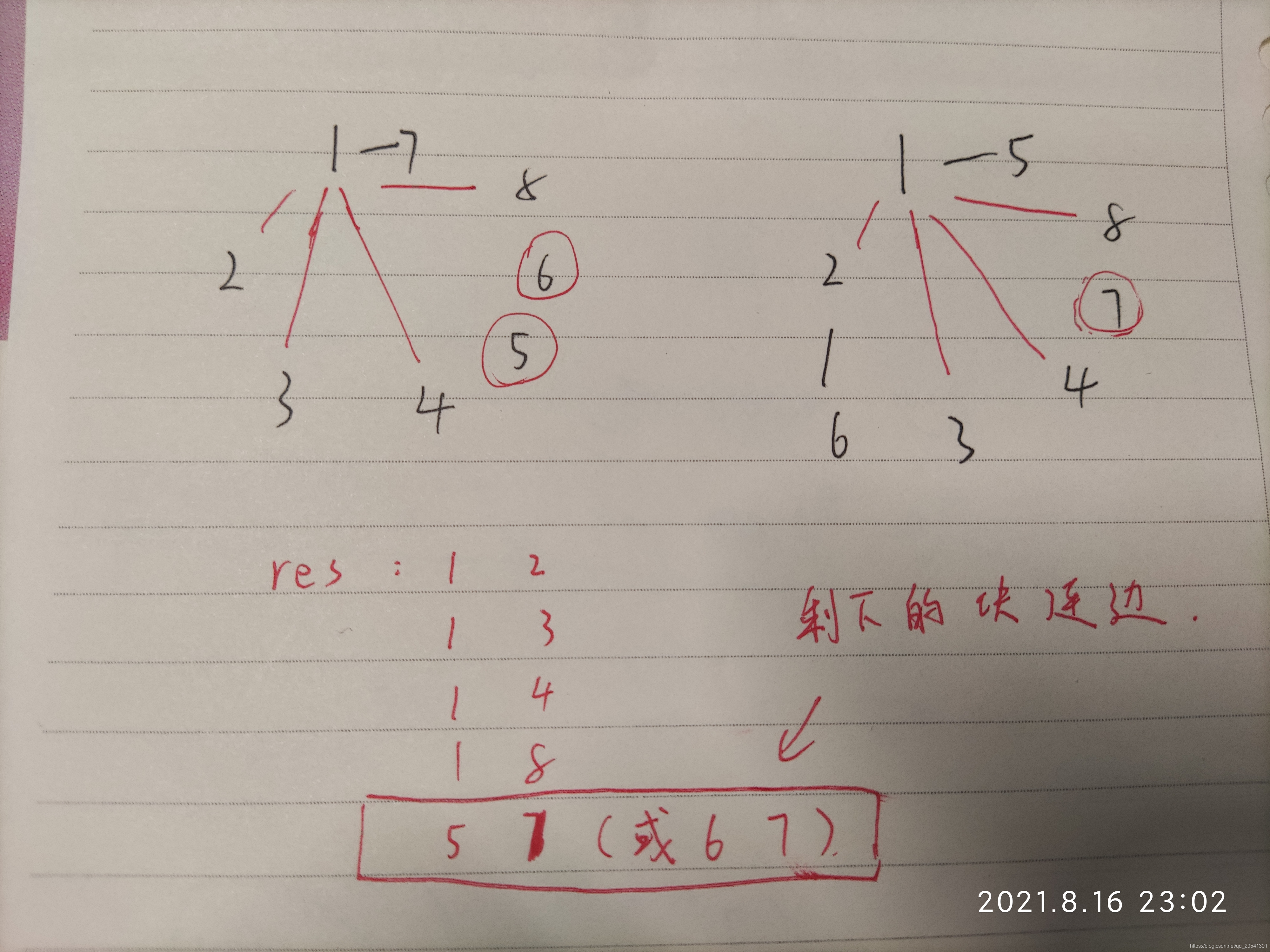
我们先找到1(当然,也可以是其他任何点)的所有可以连的边。然后再把两张图中剩下的点(或者点集)连边。
Input
8 1 2
1 7
2 6
1 5Output
5
1 2
1 3
1 4
1 8
5 7
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
#define all(x) x.begin(), x.end()
#define maxi(x) max_element(x.begin(), x.end()) - x.begin()
#define mini(x) min_element(x.begin(), x.end()) - x.begin()
struct DSU
{
std::vector<int> f, siz;
DSU(int n) : f(n), siz(n, 1) { iota(f.begin(), f.end(), 0); }
int find(int x)
{
while (x != f[x])
x = f[x] = f[f[x]];
return x;
}
bool same(int x, int y) { return find(x) == find(y); }
bool Union(int x, int y)
{
x = find(x);
y = find(y);
if (x == y)
return false;
siz[x] += siz[y];
f[y] = x;
return true;
}
int size(int x) { return siz[find(x)]; }
};
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m1, m2;
cin >> n >> m1 >> m2;
DSU t1(n + 2), t2(n + 2);
int u, v;
while (m1--)
{
cin >> u >> v;
t1.Union(u, v);
}
while (m2--)
{
cin >> u >> v;
t2.Union(u, v);
}
vector<pii> res;
for (int i = 2; i <= n; i++)
if (!t1.same(1, i) && !t2.same(1, i))
{
res.push_back({1, i});
t1.Union(1, i);
t2.Union(1, i);
}
vector<int> A, B;
for (int i = 2; i <= n; i++)
{
if (!t1.same(1, i) && t1.find(i) == i && t2.same(1, i))
A.push_back(i);
if (!t2.same(1, i) && t2.find(i) == i && t1.same(1, i))
B.push_back(i);
}
int ans = min(A.size(), B.size());
cout << res.size() + ans << endl;
for (auto x : res)
cout << x.first << " " << x.second << endl;
for (int i = 0; i < ans; i++)
cout << A[i] << " " << B[i] << endl;
return 0;
}