[开发测试]二分法查找

1.二分查找

1.是什么

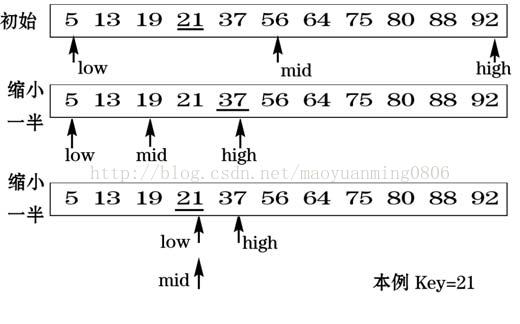
有序的序列，每次都是以序列的中间位置的数来与待查找的关键字进行比较，每次缩小一半的查找范围，直到匹配成功。

2.优缺点

优点是比较次数少，查找速度快，平均性能好；

其缺点是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

3.java实现

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

1.while循环

public static ?int search(int[] nums,int target){
 ? ?int low=0;
 ? ?int high=nums.length-1;
 ? ?int mid=0;
 ? ?while (low<=high){
 ? ? ? ?//若小于数组最小值,或者大于数组最大值,则返回-1;
 ? ? ? ?if (nums[low]>target || nums[high]<target){
 ? ? ? ? ? ?return -1;
 ? ? ?  }
 ? ? ? ?mid=(high-low)/2+low;
 ? ? ? ?//左边
 ? ? ? ?if (nums[mid]>target){
 ? ? ? ? ? ?high=mid-1;
 ? ? ? ? ? ?//右边
 ? ? ?  }else ?if (nums[mid]<target){
 ? ? ? ? ? ?low=mid+1;
 ? ? ?  }else {
 ? ? ? ? ? ?return mid;
 ? ? ?  }
 ?  }
 ? ? ? ? ? return -1;
}

2.递归实现

public ?static ?int search(int[] nums,int target,int low,int high){
 ? ? //先判断是否比最小值小,或者比最大值大,return -1;
 ? ?if (nums[low]>target || nums[high]<target){
 ? ? ? ?return -1;
 ?  }
 ? ? //取到中间的下标,防止溢出
 ? ? ?int mid=(high-low)/2+low;
 ? ?//目标值比中间的大,取右半部分
 ? ? if (nums[mid]<target){
 ? ? ? ? return search(nums,target,mid+1,high);
 ? ? ? ? //左半部分
 ? ? }else if (nums[mid]>target){
 ? ? ? ?return search(nums,target,low,mid-1);
 ? ? }else {
 ? ? ? ? return ?mid;
 ? ? }
}

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

public class Solution extends VersionControl {
 ? ?public int firstBadVersion(int n) {
 ? ? ? ?int low=1;
 ? ? ? ?int high=n;
 ? ? ? ?int mid=0;
 ? ? ? ?while(low<high){
 ? ? ? ? ? ?mid=(high-low)/2+low;
 ? ? ? ? ? ?if(isBadVersion(mid)){
 ? ? ? ? ? ? ? ?//中间是错误的版本,
 ? ? ? ? ? ? ? ?high=mid; ? //错误版本答案在[low,mid]之间
 ? ? ? ? ?  }else{
 ? ? ? ? ? ? ? ?//中间不是错误的版本
 ? ? ? ? ? ? ? ?low=mid+1; //错误版本在[mid+1,high]之间
 ? ? ? ? ?  }
 ? ? ?  }
 ? ? ? ?return low; ?//low==high
 ?  }
}

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

class Solution {
 ? ?public int searchInsert(int[] nums, int target) {
 ? ? ? ?int low=0;
 ? ? ? ?int high=nums.length-1;
 ? ? ? ?int mid=0;
 ? ? ? ?while(low<=high){
 ? ? ? ? ? ?mid=(high-low)/2+low;
 ? ? ? ? ? ?//中间值大于插入值，则插在前一半中
 ? ? ? ? ? ?if(nums[mid]>target){
 ? ? ? ? ? ? ? ?high=mid-1; //最大值为前一半
 ? ? ? ? ? ? ? ? //中间值小于插入值，则插在后一半中
 ? ? ? ? ?  }else if(nums[mid]<target){
 ? ? ? ? ? ? ? ?low=mid+1; ?//最小值以中间下标开始
 ? ? ? ? ?  }else{
 ? ? ? ? ? ? ? ?return mid; ? //返回插入值
 ? ? ? ? ?  }
 ? ? ?  }
 ? ? ? ?return nums[mid]<target?mid+1:mid; ?
 ?  }
}