[开发测试]Lingo阶段生产问题

*** 阶段生产问题
某公司生产某产品，最大生产能力为10000单位，每单位存储费2元，预定的销售量与单位成本如下：

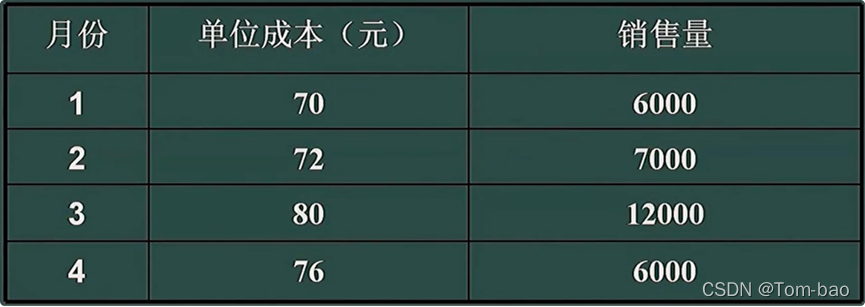
求一生产计划，使（1）满足需求；（2）不超过最大生产能力；（3）成本(生产成本与存储费之和)最低

解：假定1月初无库存，4月底卖完，当月生产的不库存，库存量无限制

模型一：
设 xi：第i个月的产量，ci：第i个月的单位成本，di：第i个月的销售量，ei：第i个月的单位存储费，a：最大生产能力
目标函数：
成本最低 <—> 生产成本和存储费之和最低

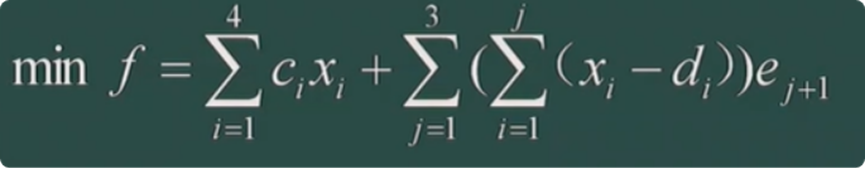
约束条件：

段编程代码：

model:
title 生产计划程序1;

sets:             ! 集合段
yue/1..4/:c, d, e, x;
endsets

data:            !数据段
a = 10000;
c = 70 72 80 76;
d = 6000 7000 12000 6000;
e = 2 2 2 2;
enddata

min = @sum(yue:c*x) + @sum(yue(j) | j#le#3: @sum(yue(i) | i#le#j:x-d)*e(j+1)); !目标函数段

@for(yue(j) | j#le#3:@sum(yue(i) | i#le#j:x-d)>0);  ! 约束段
@sum(yue:x-d) = 0;
@for(yue:x<a);                               ! 默认变量非负，且≤与＜等效
End

模型二：
设xi：第i月产量，di：销售量，ei：存储费，
ci：单位成本，si：第i月初的库存量。
目标函数：
成本最低 <—> 生产成本和存储费之和最低

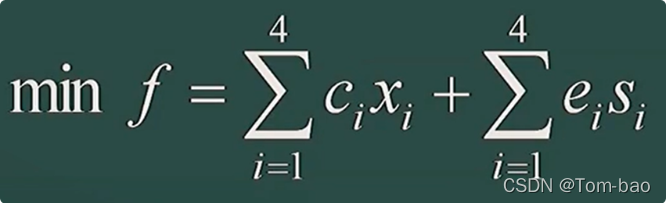
约束条件：

段编程代码：

model:
Title 生产计划程序2;

Sets:            ! 集合段
Yuefen/1..4: c, x, e, d, s;
Endsets

Data:           ! 数据段
C = 70 72 80 76;
D = 6000 8000 12000 6000;
E = 2 2 2 2;
A = 10000;
Enddata

Min = @sum(yuefen: c*x + e*s);  !目标函数段

S(1) = 0;
S(4) + x(4) – d(4) = 0;
@for(yuefen(i) | i#lt#4: s(i + 1) = s(i) + x(i) – d(i));
@foe(yuefen: x<a);
End

模型三:
化为运输问题
设 xij：第i月生产的产品在第j月卖出的数量，
cij：第i月生产的产品在第j月卖出时的生产成本与存储费之和，
dj：第j月的销售量
成本费用分析：
c11：第1月生产的产品在第1个月卖出的成本，当月卖出不会产生存储费，因此c11 = 70元；
c12：第1月生产的产品在第2个月卖出的成本，第2个月卖出时会产生一个月存储费，相应的单位成本c12为70+2=72元，其余cij类似

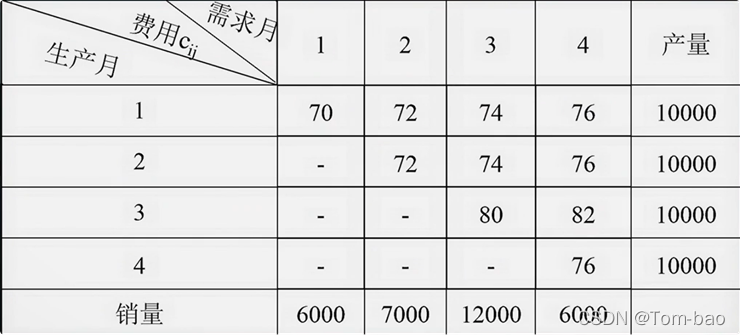
目标函数：

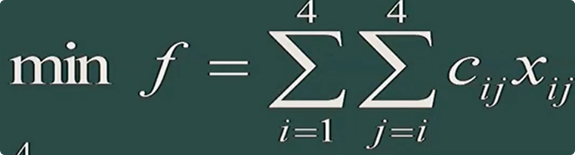
约束条件：

段编程代码：

Model:
Title 生产计划程序3;

Sets:                   ! 集合段;
Yuefen/1..4/: a, d, xx;     
Link(yuefen, yuefen) | &2#ge#&1: c, x;   ! 定义上三角矩阵;
Endsets

Data:                  ! 数据段;
c = 70 72 74 76
      71 73 75
         80 82
            76;
d = 6000 7000 12000 6000;
a = 10000 10000 10000 10000;
enddata

min = @sum(link: c*x);  ! 目标函数段;

@for(yuefen(i):@sum(yuefen(j) | j#ge#i: x(i, j))<a(i));
@for(yuefen(j):@sum(yuefen(i) | j#ge#i: x(i, j))>d(j));
@for(yuefen(i):xx = @sum(yuefen(j) | j#ge#i: x(i, j)));  !得到每个月的生产量 ;
end

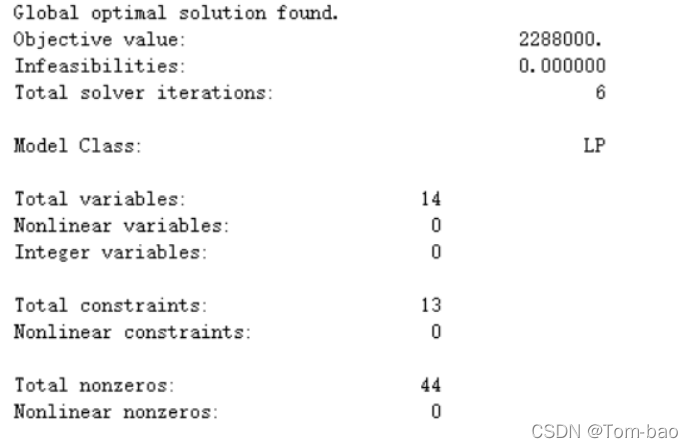
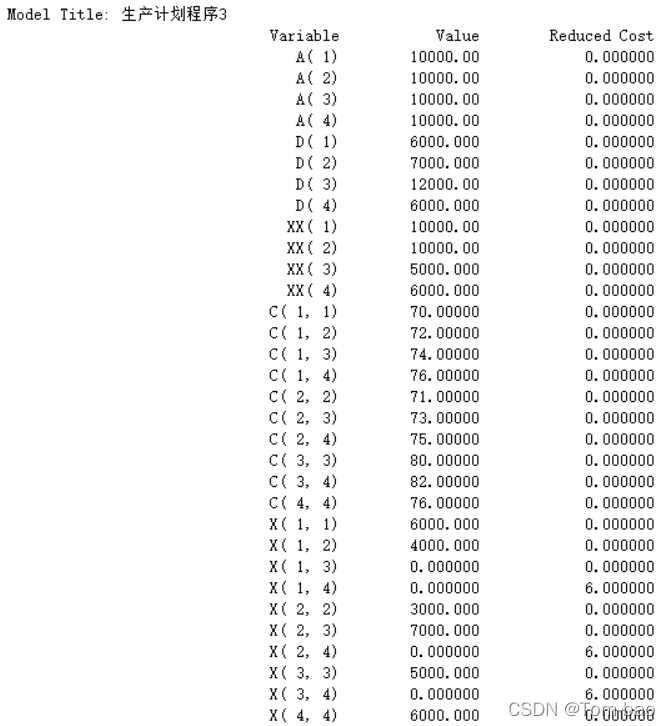
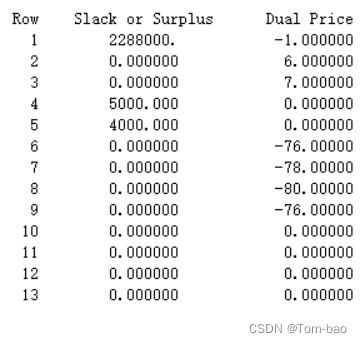
模型最优解：
1-4月份分别生产：10000、10000、5000、6000单位产品时
总成本（最低）：229.8万元

Lingo运行模型三结果：