算法设计 寻宝问题
1. 问题描述
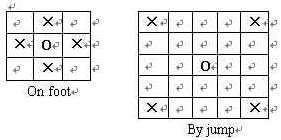
对于某个m*n的字符串数组,相当于一个m行n列的平面形状的方格。里面S表示起点,W表示障碍,B表示可走(但是不一定可以通),X表示出口。对于起点S,有8个方向可以走,当然前提是在没有障碍的情况之下,其中可以分为单步走(on foot)和跳步走(by jump)两种情况,从起点S开始追寻最短的出口路径count2。
2. 具体要求
Input
输入的第一行是一个整数n (0<=n<=20),表示测试用例的数量。下面的行是n个测试用例的数据。每个测试用例的第一行由两个整数x和y组成(0接下来的x行描述了迷宫矩阵,其中包含x行和y列。在矩阵中,“W”表示屏障,“B”表示可进入的位置,“S”表示起始位置,“X”表示方舟的位置。迷宫矩阵中只有一个S和一个X。
Output
对于每个测试用例,输出一行。如果有问题的解决方案,输出找到方舟的最少步骤的数量。否则输出“NO ANSWER”。
3. 测试数据
Sample Input
3
3 3
SWB
BWB
XBB
5 4
BXWB
BBWS
BBWB
BBWB
BBBB
3 2
WX
WW
WS
Sample Output
2
2
NO ANSWER
代码:
enum class Dir { u, r, d, l, lu, ru, ld, rd, n };
/// <summary>
/// 是否能移动到目标位置
/// </summary>
/// <param name="arr">地图</param>
/// <param name="x">数组最大横坐标</param>
/// <param name="y">数组最大纵坐标</param>
/// <param name="nextx">目标位置x</param>
/// <param name="nexty">目标位置y</param>
/// <param name="reach">标志是否已经到达过</param>
/// <returns>是否能移动到目标位置</returns>
bool can(char** arr, int x, int y, int nextx, int nexty, bool** reach)
{
if (nextx > x || nexty > y || nextx < 0 || nexty < 0) // 是否越界
{
return false;
}
if (arr[nextx][nexty] == 'W') // 是否是障碍
{
return false;
}
if (reach[nextx][nexty] == true) // 是否已经到达过
{
return false;
}
return true;
}
/// <summary>
/// 移动
/// </summary>
/// <param name="arr">地图</param>
/// <param name="x">数组最大横坐标</param>
/// <param name="y">数组最大纵坐标</param>
/// <param name="curx">当前位置x</param>
/// <param name="cury">当前位置y</param>
/// <param name="curstep">当前移动不属</param>
/// <param name="dir">移动方向</param>
/// <param name="reach">标志是否已经到达过</param>
/// <param name="minstep">最小步数</param>
/// <returns></returns>
bool go(char** arr, int x, int y, int curx, int cury, int curstep, Dir dir, bool** reach, int& minstep)
{
reach[curx][cury] = true;
if (arr[curx][cury] == 'X') // 找到终点
{
if (curstep < minstep)
{
minstep = curstep;
}
reach[curx][cury] = false; // 回溯,清空已达的标记
return true;
}
else
{
bool flag = false;
bool tmp = false;
if (can(arr, x, y, curx - 1, cury, reach)) // up
{
tmp = go(arr, x, y, curx - 1, cury, curstep + 1, Dir::u, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx, cury + 1, reach)) // right
{
tmp = go(arr, x, y, curx, cury + 1, curstep + 1, Dir::r, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx + 1, cury, reach)) // down
{
tmp = go(arr, x, y, curx + 1, cury, curstep + 1, Dir::d, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx, cury - 1, reach)) // left
{
tmp = go(arr, x, y, curx, cury - 1, curstep + 1, Dir::l, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx - 2, cury - 2, reach)) // left up
{
tmp = go(arr, x, y, curx - 2, cury - 2, curstep + 1, Dir::lu, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx - 2, cury + 2, reach)) // right up
{
tmp = go(arr, x, y, curx - 2, curx + 2, curstep + 1, Dir::ru, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx + 2, cury - 2, reach)) // left down
{
tmp = go(arr, x, y, curx + 2, cury - 2, curstep + 1, Dir::ld, reach, minstep);
flag = flag == true ? true : tmp;
}
if (can(arr, x, y, curx + 2, cury + 2, reach)) // right down
{
tmp = go(arr, x, y, curx + 2, cury + 2, curstep + 1, Dir::rd, reach, minstep);
flag = flag == true ? true : tmp;
}
reach[curx][cury] = false; // 回溯,清空已达的标记
return flag;
}
}
void test1()
{
int n;
cin >> n;
while (n--)
{
int x, y;
cin >> x >> y;
char** arr = new char* [x];
bool** reach = new bool* [x];
for (int i = 0; i < x; i++)
{
arr[i] = new char[y];
reach[i] = new bool[y];
}
int sx = 0, sy = 0;
for (int i = 0; i < x; i++)
{
for (int j = 0; j < y; j++)
{
cin >> arr[i][j];
if (arr[i][j] == 'S')
{
sx = i;
sy = j;
}
reach[i][j] = false;
}
}
int minstep = INT_MAX;
if (go(arr, x - 1, y - 1, sx, sy, 0, Dir::n, reach, minstep))
{
cout << minstep << endl;
}
else
{
cout << "NO ANSWER" << endl;
}
for (int i = 0; i < x; i++)
{
delete[] arr[i];
}
delete[] arr;
delete[] reach;
}
}
截图: