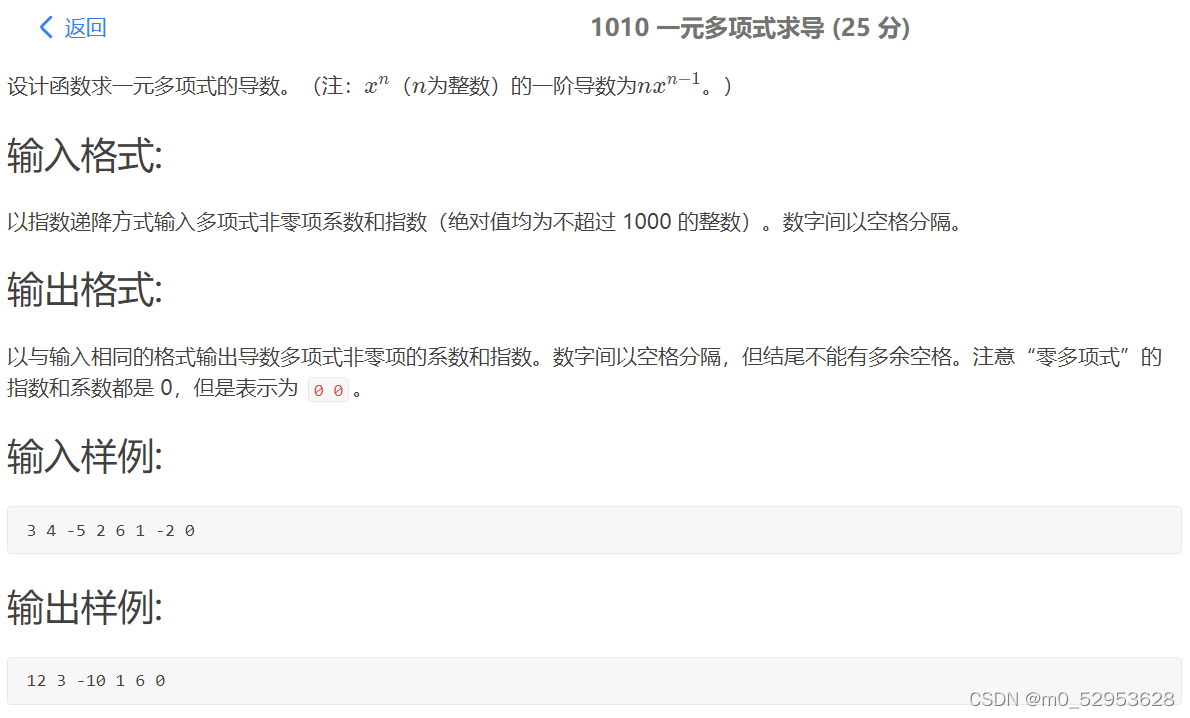
该题解题思路:
1、输入两个数,判断是否为0,分情况讨论。
2、进入循环,验证所有事例。

该题解题思路:
1、根据大小比较输出不同的结果;
2、注意定义的数据类型;

该题解题思路:
1、循环之后判断;
2、判断属于哪种情况按条件输出;
翻译:
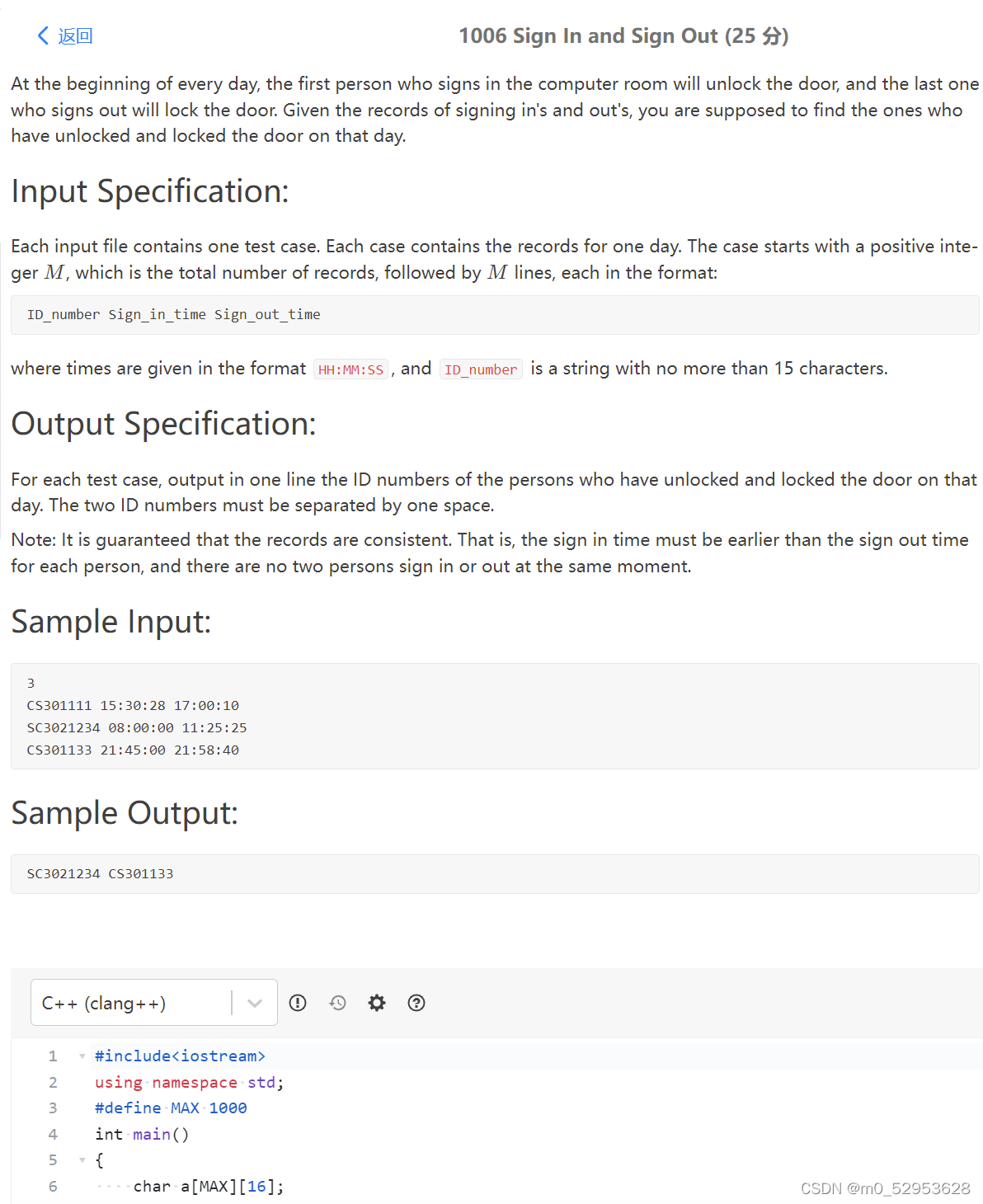
1006登录和注销(25分)
在每天开始的时候,第一个在计算机室签名的人会打开门,最后一个签名的人会锁上门。根据登录和注销的记录,你应该找到当天解锁和锁门的人。
输入规格:
每个输入文件包含一个测试用例。每个案例包含一天的记录。案例以一个正整数M开始,它是记录的总数,后跟M行,每行的格式如下:
身份证号码签到时间签到时间
其中时间以HH:MM:SS格式给出,ID_编号为不超过15个字符的字符串。
输出规格:
对于每个测试用例,在一行中输出当天解锁和锁闭车门的人员的ID号。两个ID号必须用一个空格分隔。
注:保证记录的一致性。也就是说,每个人的登录时间必须早于注销时间,并且没有两个人同时登录或注销。
样本输入:
3.
CS301111 15:30:28 17:00:10
SC3021234 08:00:00 11:25:25
CS301133 21:45:00 21:58:40
样本输出:
SC3021234 CS301133
该题解题思路:
1、计算时间,都换算成秒;
2、比较大小;
翻译:
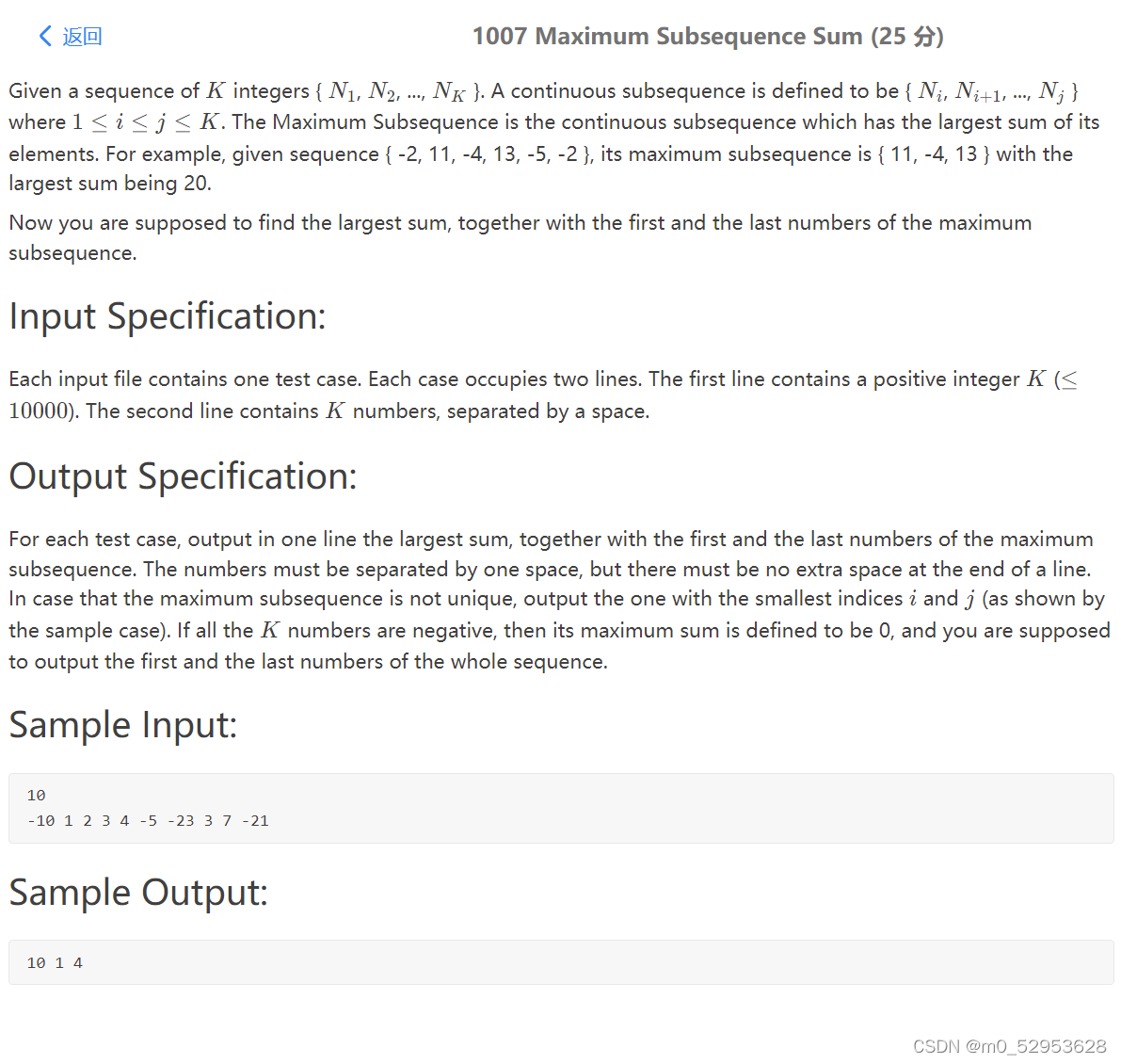
1007最大子序列和
给定一个K整数序列{N1.N2., …, NK}.连续子序列定义为{Ni,Ni+1, …, NJ}其中1≤我≤J≤K.最大子序列是其元素之和最大的连续子序列。例如,给定序列{-2,11,-4,13,-5,-2},其最大子序列为{11,-4,13},最大和为20。
现在你应该找到最大和,以及最大子序列的第一个和最后一个数。
输入规格:
每个输入文件包含一个测试用例。每个箱子占两行。第一行包含一个正整数K(≤10000). 第二行包含K个数字,用空格分隔。
输出规格:
对于每个测试用例,在一行中输出最大和,以及最大子序列的第一个和最后一个数字。数字之间必须用一个空格隔开,但在一行的末尾不能有额外的空格。如果最大子序列不是唯一的,则输出具有最小索引i和j的子序列(如示例案例所示)。如果所有的K个数都是负数,那么它的最大和被定义为0,并且你应该输出整个序列的第一个和最后一个数。
样本输入:
10
-10 1 2 3 4 -5 -23 3 7 -21
样本输出:
10 1 4
该题解题思路:
1、设置一个sum数组,用来存放第N个位置的前N项和
2、第一次循环接受输入,第二次循环处理数组,填充sum数组,,第三次循环更新shortest值、最大子序列和的值、最大和子序列的开始和结束位置;
翻译:
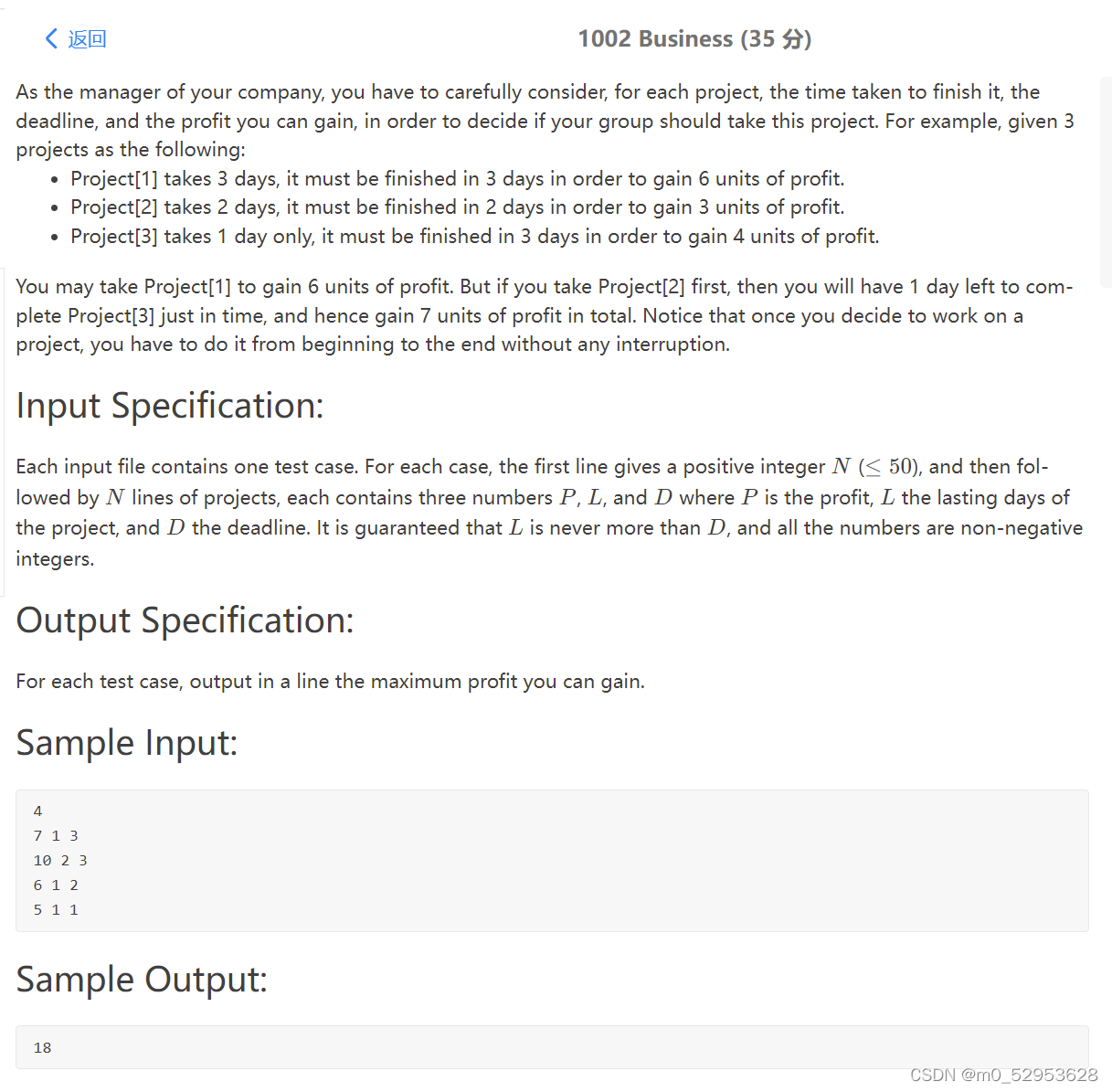
作为贵公司的经理,你必须仔细考虑每一个项目,完成它的时间,截止日期,以及你能获得的利润,以便决定你的团队是否应该接受这个项目。例如,给定以下3个项目:
项目[1]需要3天,必须在3天内完成,才能获得6个单位的利润。
项目[2]需要2天,必须在2天内完成,才能获得3个单位的利润。
项目[3]只需1天,必须在3天内完成,才能获得4个单位的利润。
您可以通过项目[1]获得6个单位的利润。但如果您先完成项目[2],那么您将有1天的时间及时完成项目[3],从而总共获得7个单位的利润。请注意,一旦您决定进行一个项目,您必须从头到尾不间断地进行。
输入规格:
每个输入文件包含一个测试用例。对于每种情况,第一行给出一个正整数N(≤50),然后是N行项目,每个项目包含三个数字P、L和D,其中P是利润,L是项目的持续天数,D是截止日期。保证L永远不超过D,并且所有的数字都是非负整数。
输出规格:
对于每个测试用例,在一行中输出您可以获得的最大利润。
样本输入:
4.
7 1 3
10 2 3
6 1 2
5 1 1
样本输出:
18
该题解题思路:
n为项目个数
m为总天数(为最晚的那个截止日期)
dp[i][j]表示第j天能在前i个项目获得的最大利润,初始均为0。
首先将项目按照ddl进行排序,现在对第 i 个项目,j 从第一天开始,如果可以在第 j 天结束做这个项目,那么开始做个这项目的时间 t = (截止日期和 j 中较小的数)- 项目所需时间,则 t 大于等于 0 ,才可以在第 j 天完成这个项目。
当 t >= 0 的时候,dp[i][j] = max(dp[i-1][j], dp[i-1][t]+第i个项目的利润),简单来讲,就是两种情况,一种不做项目 i ,那么利润为第j天在前i-1中获得的最大项目,即dp[i-1][j];另一种,做这个项目,但是因为最晚是从第 t 天开始做这个项目,所以利用为第t天在前i-1中获得的最大项目 + 该项目的利润,即dp[i-1][t]+v[i-1].p(代码中v是从0开始的,所以第i个项目对应v[i-1])。
当 t < 0, 说明不可以在第j天内完成这个项目,所以dp[i][j] = dp[i-1][j]