在Unity中,矩形的区域检测很简单,使用Rect.Contans就可以判断。但是,这仅限于平行于坐标轴的矩形区域。假如矩形图像旋转了,区域判断就不能简单的使用Rect.Contans判断了,否则会出现错误的检测结果。在游戏中,这是很常见的问题,旋转矩形的区域判断很常用。但是,这在Unity中做旋转矩形区域的区域判断,就没有给出直接的方法。笔者这段时间碰到这个问题,苦恼于不能做旋转矩形的区域判断,后来请教了做相关工作的大佬,得到启发。而后写出了旋转矩形区域判断案例,发布在CSDN资源上。现在就以此案例为背景,介绍实现旋转矩形的区域检测。
首先上图演示实现的效果和上资源链接:

?图1 - 效果演示图
资源链接:
https://download.csdn.net/download/a95537709/20334843?spm=1001.2014.3001.5501
下面开始介绍旋转矩形的区域检测的向量叉积算法。
一、平面向量、空间向量、三角函数、向量点积、向量叉积
平面向量、空间向量、三角函数、向量点积、向量叉积是读懂本文方法的必备基础知识。这些知识我们在初中、高中数学都学习过。如果这些知识多年没用过,你可能像我一样已经忘干净了。这样的话我们需要温习一下这些知识点,着重温习向量叉积的定义和几何意义,你需要在搜索引擎中找到这些知识重温一下。
二、多边形区域检测的叉积算法
多边形区域检测的叉积算法,说白了,就是一个公式,本文使用的这个公式,来源于一篇博客文章,标题:判断 点 与直线与矩形的关系。链接:https://www.cnblogs.com/ant-wjf/archive/2013/04/20/3032898.html
在这里引用原文内容:
---------------------------------------------------------------------------------------------------------------------------------
判断点是否在矩形、多边形中
方法1
注:该方法适用于矩形的四个内角都小于180°
只要判断该点的横坐标和纵坐标是否夹在矩形的左右边和上下边之间。
例如:矩形四个顶点P1,P2,P3,P4,判断P是否包含在矩形中,
只需要判断:(|P2P|×|P2P1|)*(|P3P|×|P3P4|)<=0 and (|P1P|×|P1P4|)*(|P2P|×|P2P3|)<=0
---------------------------------------------------------------------------------------------------------------------------------
注意最后这一行公式,它表达的意思是向量|P2P|×|P2P1|与向量|P3P|×|P3P4|方向相反,并且向量|P1P|×|P1P4|与向量|P2P|×|P2P3|方向相反。只要满足这两个条件,P点就在矩形内。你可以根据向量叉积的定义,用右手螺旋法则试试。当且仅当P点在矩形范围内,上式成立。
三、案例的具体实现步骤
1.案例基本组件

图 2 - 基本组件
如图红框所示,案例中有两个脚本文件。FTexture为对Unity的Texture类的封装,代码参看工程文件。FreeLine为线段图像类,使用FTexture进行图像渲染。其中Refresh函数刷新组件数据和图像,在这个函数里,计算出矩形区域旋转后的四个端点。然后IsEnter函数用矩形的四个端点和上文提到的向量叉积公式计算出活动点是否在矩形区域内。矩形四个端点计算代码如下,详细解说在后文。

??图 3?- 矩形四个端点PA、PB、PC、PD的计算代码
2.找到旋转矩形的四个端点(支持向量叉积算法的必备条件)
假设你已经知道矩形区域叉积算法了,到你真正写起代码的时候你会发现:这个算法实现的难点不在于向量叉积算法的公式,而在于找到旋转矩形的四个端点。因为向量叉积算法的公式已经明确,把四个端点加一个活动点往公式一代入就可以计算出结果了。代入公式计算,就是以下如图所示的几行代码:

?图 4?- 使用向量叉积算法公式计算是否在区域范围内
圆规正传,现在我们来看看如何找到(计算出)矩形旋转后的四个端点。

?图 5 - 矩形旋转前后示意图
图中,绿色方框为矩形原始方位图,红色方框为方框旋转后的矩形图。O点为原点、旋转的中心点,位置为Pivot=(0.0f,?0.5f),A、B、C、D为矩形旋转后的四个端点。旋转角度为:逆时针旋转a度(angle度。这里用了60度,便于区分)。
首先,我们来计算A点坐标PA。做辅助线如图6所示

图 6?
![]()
这里的LineWidth是(线宽)直线的高度,OA是线宽的一半,?由正弦余弦定理定理,可得到:
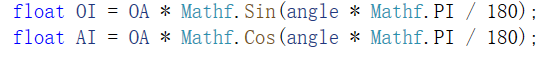
?由此可得:

StartPosition是O点坐标(线段的起点),pA = new Vector2(-pAx, -pAy),为什么是-pAx,看图6。从绿方框移动到红方框位置,相对于原点O,A点x坐标是负值,算出的pAx是绝对值,所以是-pAx。为什么是-pAy。看图6。从绿方框移动到红方框位置,相对于原点O,A点y坐标是负值(注意GUI的原点在左上角),算出的pAy是绝对值,所以是-pAy。这样,A点坐标就算出来了。案例用一个蓝色的圆圈圈出来了,便于观察(如图1所示矩形四个端点有蓝色圆圈圈出)。
然后,我们来计算D点坐标PD。做辅助线如图7所示

?图 7
观察可得:
![]()
由正弦余弦定理可得:
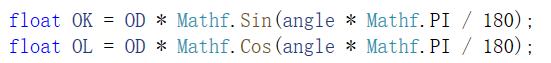
?由上可得:

?pD = new Vector2(pDx, pDy),为什么是pDx,看图7。从绿方框移动到红方框位置,相对于原点O,D点x坐标是正值,算出的pDx是绝对值,所以是pDx。为什么是pDy。看图7。从绿方框移动到红方框位置,相对于原点O,D点y坐标是正值(注意GUI的原点在左上角),算出的pDy是绝对值,所以是pDy。这样,D点坐标就算出来了。
然后,我们来计算B点坐标PB。做辅助线如图8所示

?图 8
由余弦定理、正切定理,可得:
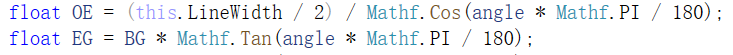
注意,在0~360度内,EG在angle角度等于?90、270度时,正切公式没有意义,EG长度为this.Length,就是线段长度。
由余弦定理、正切定理,可得:
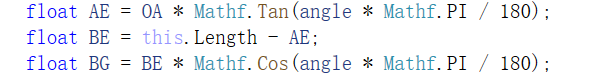
由图中观察,我们可得:

?pB = new Vector2(pBx, -pBy),为什么是pBx,看图7。从绿方框移动到红方框位置,相对于原点O,B点x坐标是正值,算出的pBx是绝对值,所以是pBx。为什么是-pBy。看图7。从绿方框移动到红方框位置,相对于原点O,B点y坐标是负值(注意GUI的原点在左上角),算出的pBy是绝对值,所以是-pBy。这样,B点坐标就算出来了。
最后,我们来计算C点坐标PC。做辅助线如图9所示

图 9
由正弦余弦定理可得:

?再由图中观察可得:

?pC?= new Vector2(pCx, -pCy),为什么是pCx,看图7。从绿方框移动到红方框位置,相对于原点O,C点x坐标是正值,算出的pCx是绝对值,所以是pCx。为什么是-pCy。看图7。从绿方框移动到红方框位置,相对于原点O,C点y坐标是负值(注意GUI的原点在左上角),算出的pCy是绝对值,所以是-pCy。这样,C点坐标就算出来了。
至此,旋转后矩形的四个点PA、PB、PC、PD都算出来了。
3.以4个端点+1个活动的点为原始数据,运用向量叉积算法实现旋转矩形区域检测
找到(计算出)了矩形旋转后的四个端点,加上活动的点P(光标位置),代入上文所提的向量叉积算法公式(|P2P|×|P2P1|)*(|P3P|×|P3P4|)<=0 and (|P1P|×|P1P4|)*(|P2P|×|P2P3|)<=0(代码见图3),就可以得出区域检测的正确结果。区域检测效果如图1所示。
总结:运用叉积公式,关键在于计算出旋转后的四个端点。找出端点后直接代入公式即可得出结果。笔者计算四个端点的方法不见得是最好最快的方法,可能还是笨人的方法,但确实能达到需要的效果。如果你有更好的方法,欢迎留言分享!
欢迎转载,转载请注明出处。