[游戏开发]unity之贝塞尔曲线

简介

什么是贝塞尔曲线
贝塞尔曲线(Bezier curve)，又称 贝兹曲线 或 贝济埃曲线 ，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，当时主要用于汽车主体设计。现主要应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，比如PhotoShop中的钢笔工具。在unity中我们一般用来生成弯路的路径点或者导弹移动轨迹等等。
什么是阶（次）
两种理解：
1、贝塞尔曲线，它的背后是一个数学函数，N阶可以理解为N次方的意思，我们也可以把三阶贝塞尔曲线叫做三次贝塞尔曲线。
2、二阶贝塞尔曲线就是在一阶贝塞尔曲线的基础上再求一次一阶贝塞尔曲线；三阶贝塞尔曲线就是在二阶贝塞尔曲线的基础上再求一次一阶贝塞尔曲线；以此类推。
简单来说就是套娃。

使用

首先要传入控制点。

    public Transform[] points;

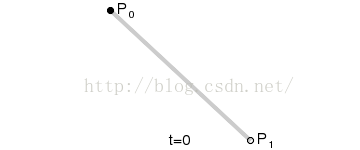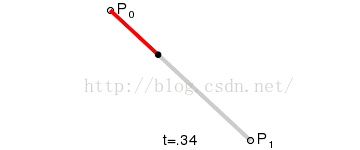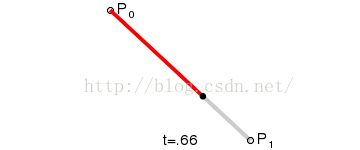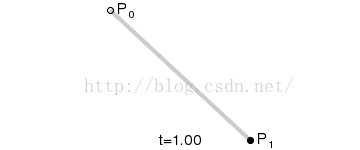
一阶贝塞尔曲线算法:

public Vector3 lineBezier(float t)
{
    Vector3 a = points[0].position;
    Vector3 b = points[1].position;
    return a + (b - a) * t;
}

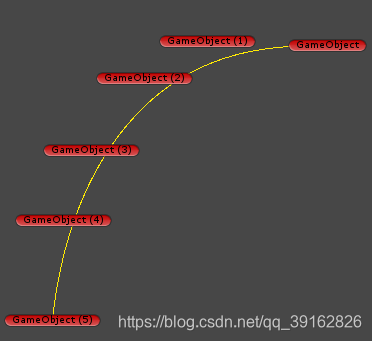
效果图

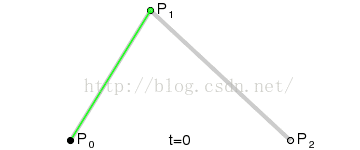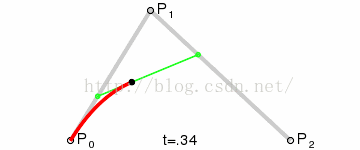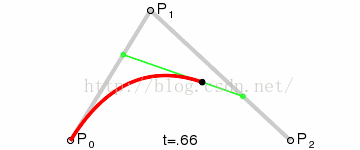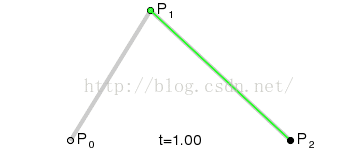
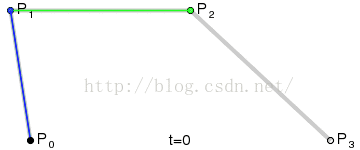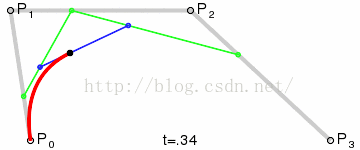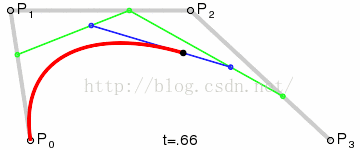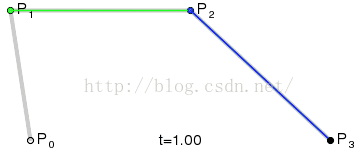
二阶贝塞尔曲线算法:

public Vector3 quardaticBezier(float t)
{
    Vector3 a = points[0].position;
    Vector3 b = points[1].position;
    Vector3 c = points[2].position;

    Vector3 aa = a + (b - a) * t;
    Vector3 bb = b + (c - b) * t;
    return aa + (bb - aa) * t;
}

效果图

三阶贝塞尔曲线算法:

public Vector3 cubicBezier(float t)
{
    Vector3 a = points[0].position;
    Vector3 b = points[1].position;
    Vector3 c = points[2].position;
    Vector3 d = points[3].position;

    Vector3 aa = a + (b - a) * t;
    Vector3 bb = b + (c - b) * t;
    Vector3 cc = c + (d - c) * t;

    Vector3 aaa = aa + (bb - aa) * t;
    Vector3 bbb = bb + (cc - bb) * t;
    return aaa + (bbb - aaa) * t;
}

效果图

以此类推。

扩展

贝塞尔曲线返回点的贝塞尔函数，使用线性插值的概念作为基础。下面我们使用Vector3.Lerp实现贝塞尔曲线在编辑器模式下生成路径点。
代码：

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

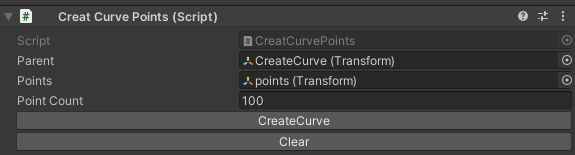
public class CreatCurvePoints : MonoBehaviour
{
    public Transform parent;
    [SerializeField] private Transform points;                          //控制点父对象
    private List<Transform> point_tranList = new List<Transform>();     //控制点列表
    [SerializeField] private int pointCount = 100;                      //曲线点的个数
    [HideInInspector]
    public List<Vector3> line_pointList;                               //曲线点列表

    public void Init()
    {
        if (null != points && point_tranList.Count == 0)
        {
            foreach (Transform item in points)
            {
                point_tranList.Add(item);
            }
        }
        line_pointList = new List<Vector3>();
        for (int i = 0; point_tranList.Count != 0 && i < pointCount; i++)
        {
            Vector3 pos1 = Vector3.Lerp(point_tranList[0].position, point_tranList[1].position, i / (float)pointCount);
            Vector3 pos2 = Vector3.Lerp(point_tranList[1].position, point_tranList[2].position, i / (float)pointCount);
            Vector3 pos3 = Vector3.Lerp(point_tranList[2].position, point_tranList[3].position, i / (float)pointCount);
            Vector3 pos4 = Vector3.Lerp(point_tranList[3].position, point_tranList[4].position, i / (float)pointCount);
            Vector3 pos5 = Vector3.Lerp(point_tranList[4].position, point_tranList[5].position, i / (float)pointCount);

            var pos1_0 = Vector3.Lerp(pos1, pos2, i / (float)pointCount);
            var pos1_1 = Vector3.Lerp(pos2, pos3, i / (float)pointCount);
            var pos1_2 = Vector3.Lerp(pos3, pos4, i / (float)pointCount);
            var pos1_3 = Vector3.Lerp(pos4, pos5, i / (float)pointCount);
            
            var pos2_0 = Vector3.Lerp(pos1_0, pos1_1, i / (float)pointCount);
            var pos2_1 = Vector3.Lerp(pos1_1, pos1_2, i / (float)pointCount);
            var pos2_2 = Vector3.Lerp(pos1_2, pos1_3, i / (float)pointCount);
            
            var pos3_0 = Vector3.Lerp(pos2_0, pos2_1, i / (float)pointCount);
            var pos3_1 = Vector3.Lerp(pos2_1, pos2_2, i / (float)pointCount);
            
            Vector3 find = Vector3.Lerp(pos3_0, pos3_1, i / (float)pointCount);

            line_pointList.Add(find);
        }
    }

    //在scene视图显示
    void OnDrawGizmos()
    {
        Init();
        Gizmos.color = Color.yellow;
        for (int i = 0; i < line_pointList.Count - 1; i++)
        {
            Gizmos.DrawLine(line_pointList[i], line_pointList[i + 1]);
        }
    }
}

#if UNITY_EDITOR
[CustomEditor(typeof(CreatCurvePoints))]
public class CreatCurvePointsEditor : Editor
{
    public override void OnInspectorGUI()
    {
        base.OnInspectorGUI();
        var ccp = target as CreatCurvePoints;
		
		//创建点
        if (GUILayout.Button("CreateCurve"))
        {
            ccp.Init();

            ccp.line_pointList.ForEach(_ =>
            {
                GameObject obj = new GameObject();
                obj.transform.SetParent(ccp.parent);
                obj.transform.position = _;
                obj.transform.rotation = Quaternion.Euler(Vector3.zero);
                obj.transform.localScale = Vector3.zero;
            });
        }

		//清除点
        if (GUILayout.Button("Clear"))
        {
            Transform parent = ccp.parent;
            for (int i = parent.childCount; i >= 1; i--)
            {
                DestroyImmediate(parent.GetChild(i - 1).gameObject, true);
            }
        }
    }
}
#endif

检视面板

效果图