16 Recommender System
16-1 Problem formulation
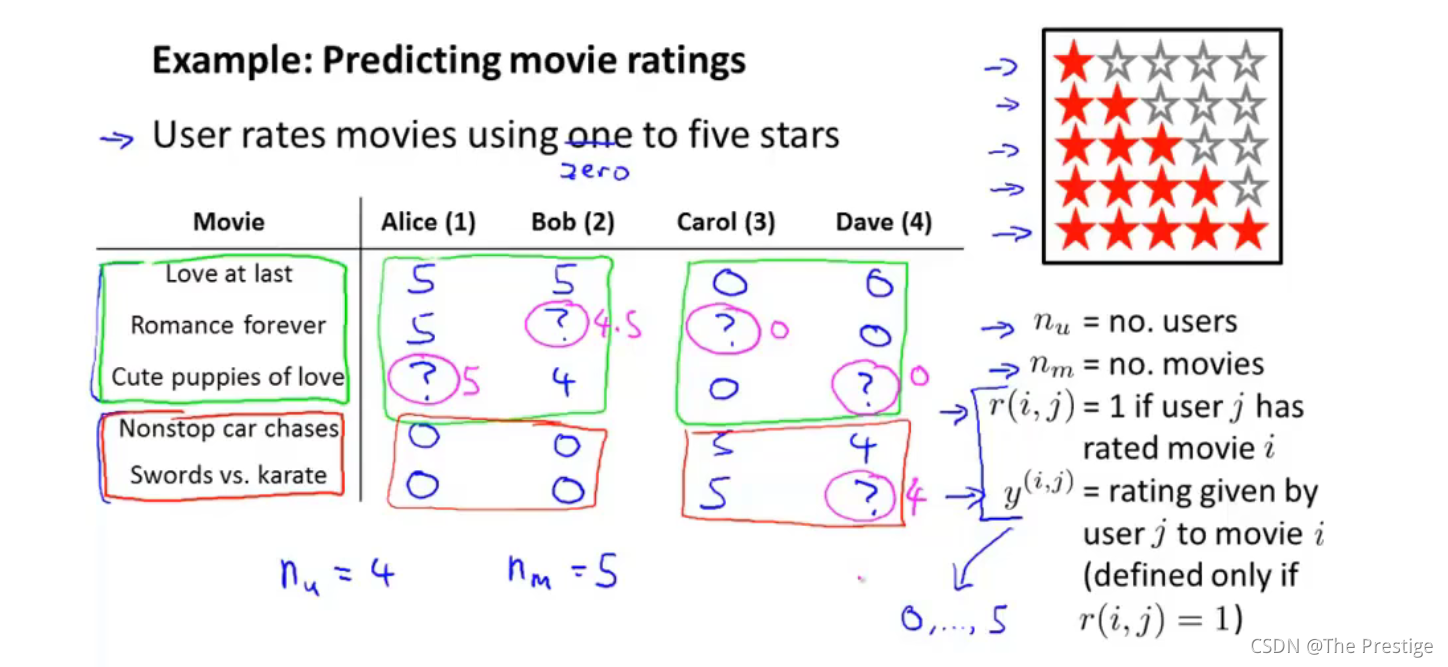
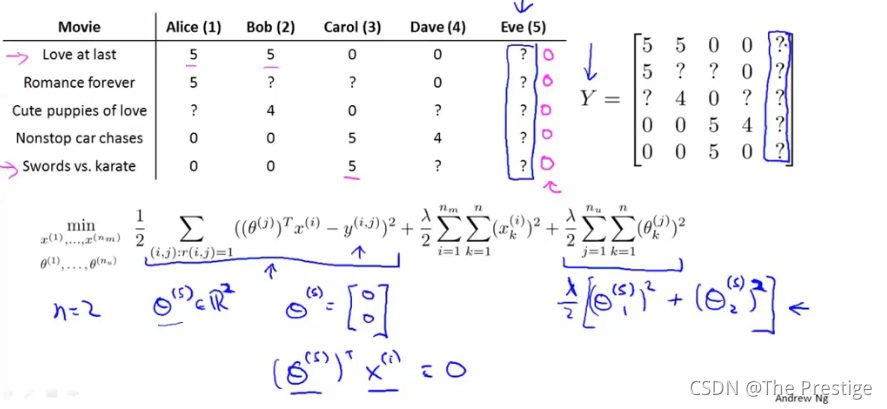
Example : predicting movie rating
User rates movies using one to five stars
16-2 Content-based recommendations
content-based recommender systems
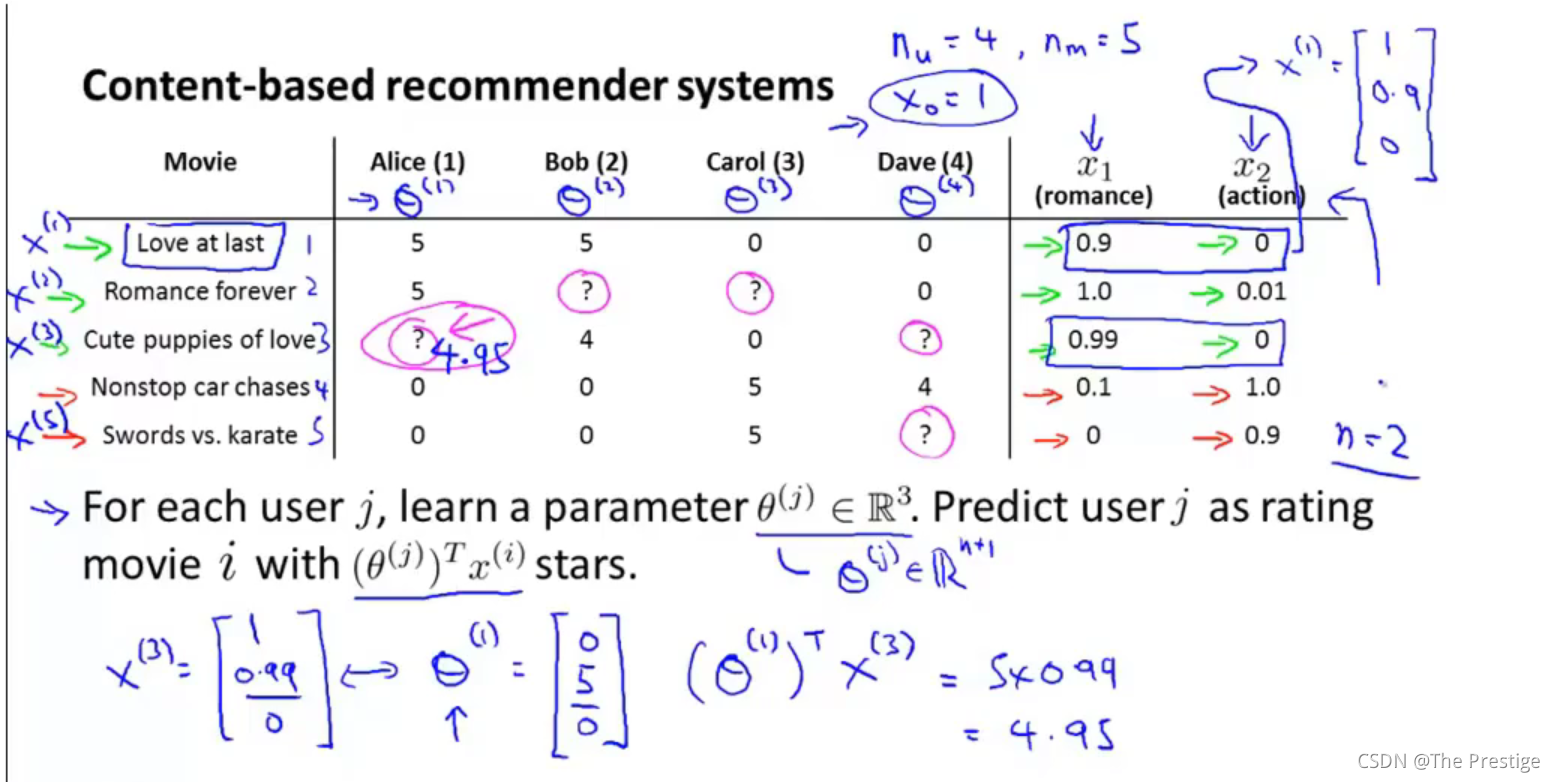
Problem formulation
$r(i,j)=$1 if user j has movie i (0,otherwise)
y ( i , j ) y^{(i,j)} y(i,j) =rating by user j on movie i (if defined)
θ ( j ) \theta^{(j)} θ(j)=parameter vector for user j
x ( j ) x^{(j)} x(j)=feature vector for movie i
For user j,movie i,predicted rating: ( θ ( j ) ) T ( x ( i ) ) (\theta^{(j)})^T(x^{(i)}) (θ(j))T(x(i))
m ( j ) = m^{(j)}= m(j)=no. of movie rated by user j
To learn θ ( j ) \theta^{(j)} θ(j):
m i n θ ( j ) 1 2 m ( j ) ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T ( x ( i ) ) ? y ( i , j ) ) 2 + λ 2 m ( j ) ∑ k = 1 n ( θ K ( j ) ) 2 \underset{\theta^{(j)}}{min}\frac{1}{2m^{(j)}}\underset{i:r(i,j)=1}{\sum}((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2+\frac{\lambda}{2m^{(j)}}\sum^{n}_{k=1}(\theta_K^{(j)})^2 θ(j)min?2m(j)1?i:r(i,j)=1∑?((θ(j))T(x(i))?y(i,j))2+2m(j)λ?∑k=1n?(θK(j)?)2 θ ( j ) ∈ R n + 1 \theta^{(j)}\in\mathbb{R}^{n+1} θ(j)∈Rn+1
Optimization objective:
To learn θ ( j ) \theta^{(j)} θ(j)(parameter for user j):
m i n θ ( j ) 1 2 ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) ? y ( i , j ) ) 2 + λ 2 ∑ k = 1 n ( θ k ( j ) ) 2 \underset{\theta^{(j)}}{min}\frac{1}{2}\underset{i:r(i,j)=1}{\sum} ( ( \theta ^ { ( j ) } ) ^ { T } x ^ { ( i ) } - y ^ { ( i , j ) } ) ^ { 2 } + \frac { \lambda } { 2 } \sum _ { k = 1 } ^ { n } ( \theta _ { k } ^ { ( j ) } ) ^ { 2 } θ(j)min?21?i:r(i,j)=1∑?((θ(j))Tx(i)?y(i,j))2+2λ?k=1∑n?(θk(j)?)2
To learn θ ( 1 ) , θ ( 2 ) , ? ? , θ ( n u ) : \theta^{(1)},\theta^{(2)},\cdots,\theta^{(n_u)}: θ(1),θ(2),?,θ(nu?):
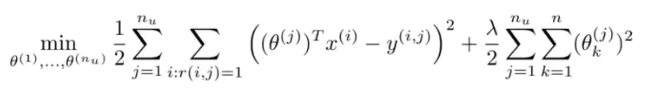

16-3 Collaborative filtering
协同过滤

16-4 Collaborative filtering algorithm
Collaborative filtering optimization objective

Collaborative filtering algorithm
-
Initialize x ( 1 ) , ? ? , x ( n m ) , θ ( 1 ) , ? ? , θ ( n u ) x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_u)} x(1),?,x(nm?),θ(1),?,θ(nu?) to small random values.
-
Minimize J ( x ( 1 ) , ? ? , x ( n m ) , θ ( 1 ) , ? ? , θ ( n u ) ) J(x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_u)}) J(x(1),?,x(nm?),θ(1),?,θ(nu?)) using gradient descent (or an advanced optimization algorithm).E.g. for every j = 1 , ? ? , n u , i = 1 , ? ? , n m j=1,\cdots,n_u,i=1,\cdots,n_m j=1,?,nu?,i=1,?,nm?:
($\color{red}\text{no loger x 0 , θ 0 x_0,\theta_0 x0?,θ0?}$)
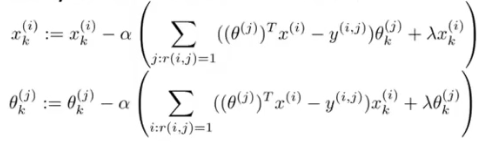
- For a user with parameters θ and a movie with (learned)
features x , predict a star rating of θ T x \theta^Tx θTx.
16-5 Vectorization: Low rank matrix factorization
低秩矩阵分解
Collaborative filtering ? \longrightarrow ?Low rank matrix factorization

Find related movies
For each product i,we learn a feature vector x ( i ) ∈ R n x^{(i)}\in\mathbb{R}^n x(i)∈Rn
find smallest ∣ ∣ x ( i ) ? x ( j ) ∣ ∣ ||x^{(i)}-x^{(j)}|| ∣∣x(i)?x(j)∣∣
16-6 Implementational detail : Mean normalization
User who have not rated any movie
Mean Normalization
