[游戏开发]delte

Chaper 03 Linear Algebra Review

3.1 Matrices and Vectors矩阵和向量

Matrices are 2-dimensional arrays:
A vector is a matrix with one column and many rows:

矩阵Matrix：Rectangular array of numbers:

Dimension of matrix: number of rows x number of columns

矩阵元素 Matrix Elements(entries of matrix)

向量 Vector: An n X 1 matrix

Notation and terms:

• A_ij refers to the element in the i^th row and j^th column of
  matrix A.

• A vector with ‘n’ rows is referred to as an ‘n’-dimensional vector.

• v_i refers to the element in the i^th row of the vector.

• In general, all our vectors and matrices will be 1-indexed. Note that for some programming languages, the arrays are 0-indexed.

• Matrices are usually denoted by uppercase names while vectors are lowercase.

• “Scalar” means that an object is a single value, not a vector or matrix.

• R refers to the set of scalar real numbers.

• Rⁿ refers to the set of n-dimensional vectors of real numbers.

Run the cell below to get familiar with the commands in Octave/Matlab. Feel free to create matrices and vectors and try out different things.

% The ; denotes we are going back to a new row.
A = [1, 2, 3; 4, 5, 6; 7, 8, 9; 10, 11, 12]

% Initialize a vector 
v = [1;2;3] 

% Get the dimension of the matrix A where m = rows and n = columns
[m,n] = size(A)

% You could also store it this way
dim_A = size(A)

% Get the dimension of the vector v 
dim_v = size(v)

% Now let's index into the 2nd row 3rd column of matrix A
A_23 = A(2,3)

3.2 Addition and scalar multiplication 加法和标量乘法

Matrix Addition

Scalar Multiplication

Combination of Operands

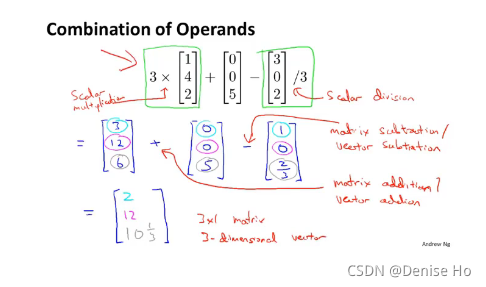
Experiment below with the Octave/Matlab commands for matrix addition and scalar multiplication. Feel free to try out different commands. Try to write out your answers for each command before running the cell below.

% Initialize matrix A and B 
A = [1, 2, 4; 5, 3, 2]
B = [1, 3, 4; 1, 1, 1]

% Initialize constant s 
s = 2

% See how element-wise addition works
add_AB = A + B 

% See how element-wise subtraction works
sub_AB = A - B

% See how scalar multiplication works
mult_As = A * s

% Divide A by s
div_As = A / s

% What happens if we have a Matrix + scalar?
add_As = A + s

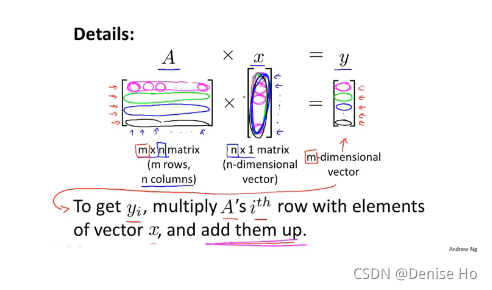
3.3 Matrix-vector multiplication 矩阵向量乘法

Example

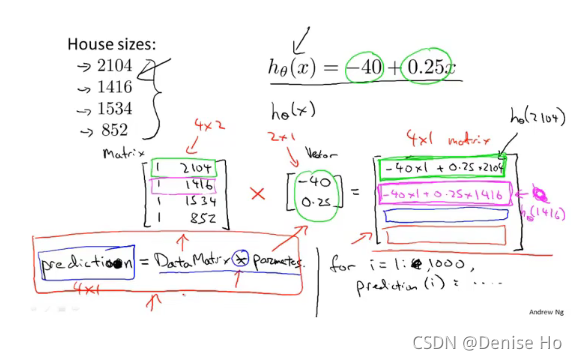
prediction = datamatrix * parameters

An m x n matrix multiplied by an n x 1 vector results in an m x 1 vector.

Below is an example of a matrix-vector multiplication. Make sure you understand how the multiplication works. Feel free to try different matrix-vector multiplications.

% Initialize matrix A 
A = [1, 2, 3; 4, 5, 6;7, 8, 9] 

% Initialize vector v 
v = [1; 1; 1] 

% Multiply A * v
Av = A * v

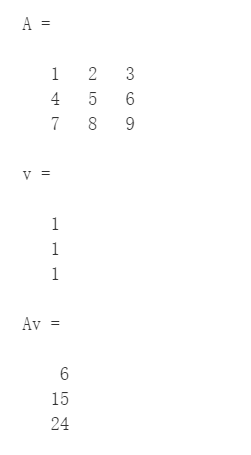
3.3 Matrix-matrix multiplication 矩阵乘法

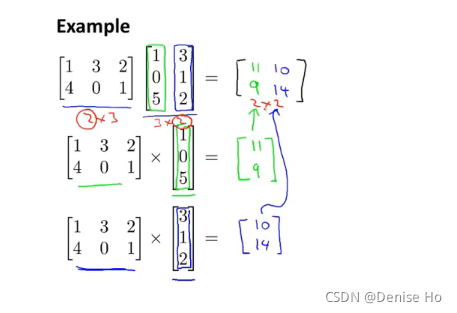
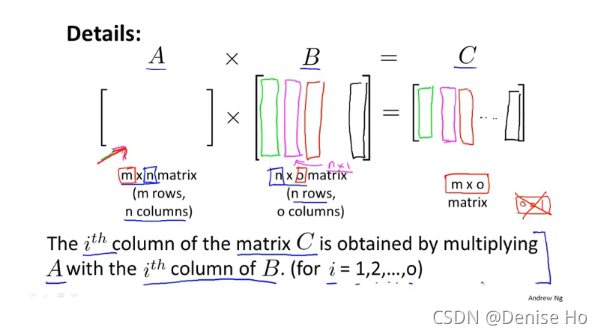
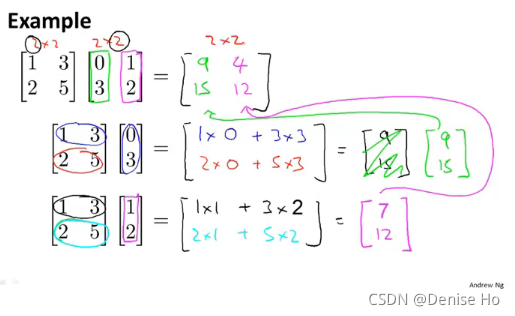
An m x n matrix multiplied by an n x o matrix results in an m x o matrix. In the above example, a 3 x 2 matrix times a 2 x 2 matrix resulted in a 3 x 2 matrix.

To multiply two matrices, the number of columns of the first matrix must equal the number of rows of the second matrix.

For example:

% Initialize a 3 by 2 matrix 
A = [1, 2; 3, 4;5, 6]

% Initialize a 2 by 1 matrix 
B = [1; 2] 

% We expect a resulting matrix of (3 by 2)*(2 by 1) = (3 by 1) 
mult_AB = A*B

% Make sure you understand why we got that result

3.5 Matrix multiplication properties 矩阵乘法特征

不满足交换律

满足结合律

Identity Matrix 单位矩阵

Matrices are not commutative: A?B != B?A
Matrices are associative: (A?B)?C = A?(B?C)

The identity matrix, when multiplied by any matrix of the same dimensions, results in the original matrix.

It’s just like multiplying numbers by 1. The identity matrix simply has 1’s on the diagonal (upper left to lower right diagonal) and 0’s elsewhere.

When multiplying the identity matrix after some matrix (A?I), the square identity matrix’s dimension should match the other matrix’s columns.

When multiplying the identity matrix before some other matrix (I?A), the square identity matrix’s dimension should match the other matrix’s rows.

% Initialize random matrices A and B 
A = [1,2;4,5]
B = [1,1;0,2]

% Initialize a 2 by 2 identity matrix
I = eye(2)

% The above notation is the same as I = [1,0;0,1]

% What happens when we multiply I*A ? 
IA = I*A 

% How about A*I ? 
AI = A*I 

% Compute A*B 
AB = A*B 

% Is it equal to B*A? 
BA = B*A 

% Note that IA = AI but AB != BA

3.5 Inverse and transpose 逆和转置

逆矩阵

A必须是方阵，不能全为0

求逆矩阵
Octave软件

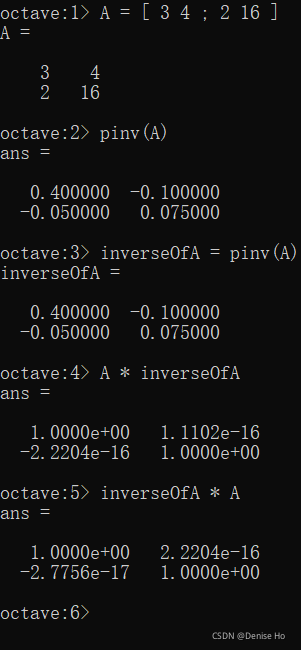
A = [ 3 4 ; 2 16 ]   // 定义矩阵A

inverseOfA = pinv(A) // 求A的逆矩阵

A * inverseOfA  // A与A的逆矩阵相乘，结果是单位矩阵I

inverseOfA * A  // A的逆矩阵相乘与A，结果是单位矩阵I

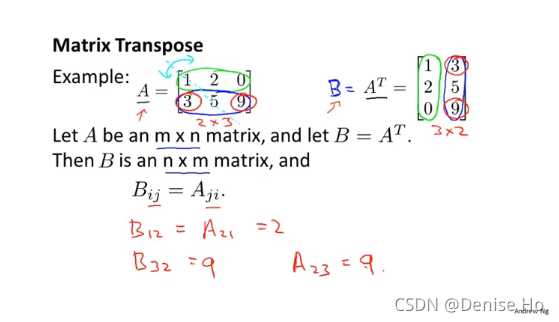
The inverse of a matrix A is denoted A^?1.
Multiplying by the inverse results in the identity matrix.

A non square matrix does not have an inverse matrix. We can compute inverses of matrices in octave with the pinv(A) function and in Matlab with the inv(A) function. Matrices that don’t have an inverse are singular or degenerate.

The transposition of a matrix is like rotating the matrix 90° in clockwise direction and then reversing it.
We can compute transposition of matrices in matlab with the transpose(A) function or A’:

In other words:

A~ij~ = A~ij~^T^

% Initialize matrix A 
A = [1,2,0;0,5,6;7,0,9]

% Transpose A 
A_trans = A' 

% Take the inverse of A 
A_inv = inv(A)

% What is A^(-1)*A? 
A_invA = inv(A)*A