? ? ?The goal of tree-based methods is to segment the feature space into a number of simple rectangular regions, to subsequently make a prediction for a given observation based on either mean or mode (mean for regression and mode for classification, to be precise) of the training observations in the region to which it belongs.
FIGURE 8.3. Top Left: A partition of two-dimensional feature space that could not result from recursive binary splitting. Top Right: The output of recursive binary splitting on a two-dimensional example. Bottom Left: A tree corresponding to the partition in the top right panel. Bottom Right: A perspective plot of the prediction surface corresponding to that tree.06_Decision Trees_01_graphviz_Gini_Entropy_Decision Tree_CART_prune_Regression_Classification_Tree_Linli522362242的专栏-CSDN博客
Unlike most other classifiers, models produced by decision trees are easy to interpret. In this chapter, we will be covering the following decision tree-based models on HR data examples for predicting whether a given employee will leave the organization in the near future or not. In this chapter, we will learn the following topics:
- Decision trees - simple model and model with class weight tuning
- Bagging (bootstrap aggregation, When sampling is performed?with?replacement)
When sampling is performed?without replacement, it is called?pasting
07_Ensemble Learning and Random Forests_Bagging_Out-of-Bag_Random Forests_Extra-Trees极端随机树_Boosting_Linli522362242的专栏-CSDN博客 - Random Forest - basic random forest and application of grid search on hyperparameter tuning
- Boosting (AdaBoost, gradient boost, extreme gradient boost - XGBoost)
- Ensemble of ensembles (with heterogeneous and homogeneous models)
Introducing decision tree classifiers
? ? ?Decision tree classifiers produce rules in simple English sentences, which can easily be interpreted and presented to senior management without any editing. Decision trees can be applied to either classification or regression problems. Based on features in data, decision tree models learn a series of questions to infer the class labels of samples.
? ? In the following figure, simple recursive decision rules have been asked by a programmer himself to do relevant actions. The actions would be based on the provided answers for each question, whether yes or no.
Terminology used in decision trees
? ? ?Decision Trees do not have much machinery as compared with logistic regression. Here we have a few metrics to study. We will majorly focus on impurity measures; decision trees split variables recursively based on set impurity criteria until they reach some stopping criteria (minimum observations per terminal node(min_samples_leaf), minimum observations for split at any node(min_samples_split), and so on):
- (cross)Entropy:?
? ? ?Here,
?is the proportion of the samples that belongs to class i for a particular node t. The entropy is therefore 0 if all samples at a node belong to the same class, and the entropy is maximal if we have a uniform class distribution.
? ? ?For example, in a binary class setting, the entropy is 0 (= -(1*0 + 0*
(0)) ) if p (i =1| t ) =1 or p(i = 0 | t ) = 0. If the classes are distributed uniformly with p (i =1| t ) = 0.5 and p(i = 0 | t ) = 0.5, the entropy is 1(= - (0.5*-1 + 0.5*-1) ) . Therefore, we can say that the entropy criterion attempts to maximize the mutual information in the tree.cp3 ML Classifiers_2_support vector_Maximum margin_soft margin_C~slack_kernel_Gini_pydot+_Infor Gai_Linli522362242的专栏-CSDN博客
? ? ?Entropy came from information theory and is the measure of impurity in data. If the sample is completely homogeneous[?ho?m??d?i?ni?s], the entropy is 0, and if the sample is equally divided, it has entropy of 1. In decision trees, the predictor with most heterogeneousness will be considered nearest to the root node to classify the given data into classes in a greedy mode. We will cover this topic in more depth in this chapter:
? ? ?Where n = number of classes. Entropy is maximum in the middle, with a value of 1 and minimum at the extremes with a value of 0. The low value of entropy is desirable, as it will segregate classes better. - Information Gain:
? ? ?Information gain is the expected reduction in entropy caused by partitioning the examples according to a given attribute. The idea is to start with mixed classes and to continue partitioning until each node reaches its observations of purest class. At every stage, the variable with maximum information gain is chosen in a greedy fashion.
Maximizing?information?gain?? ? ?In order to split the nodes at the most informative features, we need to define an objective function that we want to optimize via the tree learning algorithm. Here, our objective function is to maximize the information gain at each split, which we define as follows:
? ? ?Here, f is the feature to perform the split,
?and 
?are the dataset of the parent and jth child node, I is our impurity measure,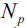 
is the total number of samples at the parent node, and 
?is the number of samples in the jth child node. As we can see, the information gain is simply the difference between the impurity of the parent node and the sum of the child node impurities—the lower the impurity of the child nodes, the larger the information gain.? ? ?However, for simplicity and to reduce the combinatorial search space, most libraries (including scikit-learn) implement binary decision trees. This means that each parent node is split into two child nodes,
Information Gain = Entropy of Parent - sum (weighted % * Entropy of Chil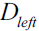d)
?and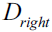 
?:
information?gain:?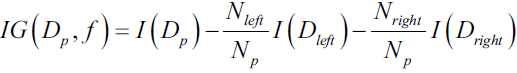
Weighted % = Number of observations in particular child/sum (observations in all
child nodes) - Gini:
? ? ?Gini impurity is a measure of misclassification, which applies in a multiclass classifier context. Gini works similar to entropy, except Gini is quicker to calculate:?? ? ?The Gini impurity can be computed by summing the probability
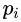?of an item with label i being chosen times the probability
?of a mistake in categorizing that item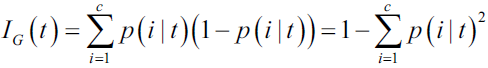
OR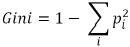
?Where i = Number of classes.
If every item in the set is in the same category, the guess will always be correct, so the error rate is 0. If there are four possible results evenly divided in the group, there’s a 75 percent chance that the guess would be incorrect, so the error rate is 0.75
p(i | t) = 1/4,? the?probability?p(i | t)?of an item with?label i?being chosen at node t,?
1- ( (1/4)^2 +?(1/4)^2 + (1/4)^2 + (1/4)^2 ) = 1- 4*0.25^2 = 1-4*0.625=1-0.25=0.75
OR 1 - 1/4 = 0.75
The similarity between Gini and entropy is shown in the following figure:
? ? ?The main difference between entropy and Gini impurity is that entropy peaks more slowly. Consequently, it tends to penalize mixed sets a little more heavily. -
Another impurity measure is the?classification error:?
?
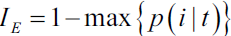? ? ?This is a useful criterion for pruning but not recommended for growing a decision tree, since it is less sensitive to changes in the class probabilities of the nodes. We can illustrate this by looking at the two possible splitting scenarios shown in the following figure:
? ? ?We start with a dataset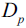
?at the parent node?that consists of 40 samples from class 1 and 40 samples from class 2 that we split into two datasets 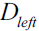?and 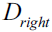?, respectively.
? ? ?The information gain using the?classification error?as a splitting criterion would be the same (?
?) in both scenario A and B:
? ? ?However, the Gini impurity??would favor the split in??scenario A(
) over?scenario B(?
), which is?indeed more pure:
https://blog.csdn.net/Linli522362242/article/details/104542381
example:?
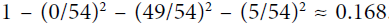and 1 == 
?+ 
?+ 
(the sum of all probabilities of all classes is equal to 1)
Decision tree working methodology from first principles
? ? ?In the following example, the response variable(target) has only two classes: whether to play tennis or not. But the following table has been compiled based on various conditions recorded on various days. Now, our task is to find out which output the variables are resulting in most significantly: YES or NO.
1. This example comes under the Classification tree:
2. Taking the Humidity[hju??m?d?ti]湿度 variable as an example to classify the Play Tennis field:
- CHAID: Humidity has two categories and our expected values should be evenly distributed in order to calculate how distinguishing the variable is:
卡方检验就是统计样本的实际观测值(Play tennis)与理论推断值(Expected)之间的偏离程度(Difference)，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。 注意：卡方检验针对分类变量
Calculating χ2 (Chi-square卡方) value:?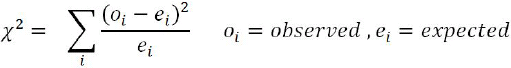
Calculating degrees of freedom = (r-1) * (c-1)
Where
????????r = number of row components or number of variable categories,
????????c = number of response variables.
Here, there are two row categories (High and Normal) and two column categories (No and
Yes).
Hence,?degrees of freedom = (r-1) * (c-1)? = (2-1) * (2-1) = 1
p-value for Chi-square?2.8 with 1 d.f = 0.0942
p-value can be obtained with the following Excel formulae: = CHIDIST (2.8, 1) = 0.0942
?from scipy import stats # https://www.graduatetutor.com/statistics-tutor/probability-density-function-pdf-and-cumulative-distribution-function-cdf/ pval = 1 - stats.chi2.cdf(2.8, 1) # Cumulative Distribution Function pval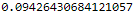
In a similar way, we will calculate the p-value for all variables and select the best variable
with a low p-value. - ENTROPY:
<==
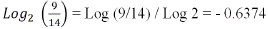
Observed Play tennis (parent node) is split by High(child or leaf node) and Normal(child or leaf node)
=0.1518
In a similar way, we will calculate information gain for all variables and select the best
variable with the highest information gain. - GINI:
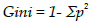OR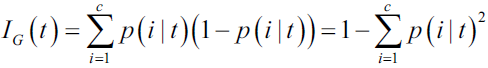
Gini_High = 1- (4/7)^2 + (3/7)^2 = 0.489
In a similar way, we will calculate Expected Gini for all variables and select the best with the
lowest expected value.
For the purpose of a better understanding, we will also do similar calculations for the Wind variable:
- CHAID: Wind has two categories and our expected values should be evenly distributed in order to calculate how distinguishing the variable is:
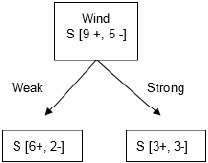
Expected = [Yes=9 ~Play tennis, No=5]
when wind is weak: [Yes=6, No=2]
When wind is strong: [Yes=3, No=3]
degrees of freedom = (r-1) * (c-1)? = (2-1) * (2-1) = 1
Where
????????r = number of row components or number of variable categories,
????????c = number of response variables.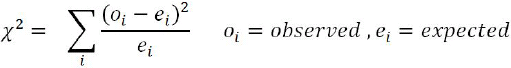
from scipy import stats # https://www.graduatetutor.com/statistics-tutor/probability-density-function-pdf-and-cumulative-distribution-function-cdf/ pval = 1 - stats.chi2.cdf(1.2, 1) # Cumulative Distribution Function pval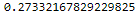
- ENTROPY:
=0.0482 - GINI:
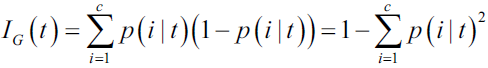
Now we will compare both variables for all three metrics so that we can understand them better.
? ? ?For all three calculations, Humidity is proven to be a better classifier than Wind. Hence, we
can confirm that all methods convey a similar story.
Comparison between logistic regression and decision trees?
? ? ?Before we?dive into the coding details of decision trees, here, we will quickly compare the differences between logistic regression and decision trees, so that we will know which model is better and in what way.
| Logistic regression | Decision trees |
| Logistic regression model looks like an equation between independent variables with respect to its dependent variable. | Tree classifiers produce rules in simple English sentences, which can be easily explained to senior management. |
| Logistic regression is a parametric model, in which the model is defined by having parameters multiplied by independent variables to predict the dependent variable. | Decision Trees are a non-parametric model, in which no pre-assumed parameter exists. Implicitly performs variable screening变量筛选 or feature selection. |
| Assumptions are made on response (or dependent) variable, with binomial or Bernoulli distribution. | No assumptions are made on the underlying distribution of the data. |
| Shape of the model is predefined (logistic curve). | Shape of the model is not predefined; model fits in best possible classification based on the data instead. |
| Provides very good results when independent variables are continuous in nature, and also linearity holds true. | Provides best results when most of the variables are categorical in nature. |
| Difficult to find complex interactions among variables (non-linear relationships between variables). | Non-linear relationships between parameters do not affect tree performance. Often uncover complex interactions. Trees can handle numerical data with highly skewed or multimodal, as well as categorical predictors with either ordinal or non-ordinal structure. |
| Outliers and missing values deteriorate[d??t?ri?re?t]恶化 the performance of logistic regression. | Outliners and missing values are dealt with grace in decision trees. |
Comparison of error components across various styles of models
? ? ?Errors need to be evaluated in order to measure the effectiveness of the model in order to
improve the model's performance further by tuning various knobs. Error components consist of a bias component, variance component, and pure white noise:?
??Out of the following three regions:
- The 1st region has high bias and low variance error components. In this region, models are very robust in nature, such as linear regression or logistic regression.
- Whereas the 3rd region has high variance and low bias error components, in this region models are very wiggly and vary greatly in nature, similar to decision trees, but due to the great amount of variability in the nature of their shape, these models tend to overfit on training data and produce less accuracy on test data.
- Last but not least, the middle region, also called the second region, is the ideal
sweet spot, in which both bias and variance components are moderate, causing it
to create the lowest total errors.
Remedial actions to push the model towards the ideal region
? ? ?Models with either high bias or high variance error components do not produce the ideal fit. Hence, some makeovers(or remedial补救的?actions) are required to do so. In the following diagram, the various methods applied are shown in detail. In the case of linear regression, there would be a high bias component, meaning the model is not flexible enough to fit some non-linearities in data. One turnaround is to break the single line into small linear pieces and fit them into the region by constraining them at knots, also called Linear Spline. Whereas decision trees have a high variance problem, meaning even a slight change in X values leads to large changes in its corresponding Y values, this issue can be resolved by performing an ensemble of the decision trees:
? ? ?In practice, implementing splines would be a difficult and not so popular method, due to the involvement of the many equations a practitioner has to keep tabs on, in addition to checking the linearity assumption and other diagnostic KPIs (p-values, AIC, multicollinearity, and so on) of each separate equation. Instead, performing ensemble on decision trees is most popular in the data science community, similar to bagging, random forest, and boosting, which we will be covering in depth in later parts of this chapter. Ensemble techniques tackle variance problems by aggregating the results from highly variable individual classifiers such as decision trees.
HR attrition data example
? ? ?In this section, we will be using IBM Watson's HR Attrition data (the data has been utilized[?ju?t?la?zd利用 in the book after taking prior permission from the data administrator) shared in Kaggle datasets under open source license agreement IBM HR Analytics Employee Attrition & Performance | Kaggle to predict whether employees would attrite[?t?ra?t]磨损以便使…变小,减员? or not based on independent explanatory variables:
import pandas as pd
hr_attr_data = pd.read_csv("./data/WA_Fn-UseC_-HR-Employee-Attrition.csv")
hr_attr_data.head()? ? ?There are about 1470 observations and 35 variables in this data, the top five rows are shown
here for a quick glance of the variables:
? ? ?The following code is used to convert Yes or No categories into 1 and 0 for modeling purposes, as scikit-learn does not fit the model on character/categorical variables directly, hence dummy coding is required to be performed for utilizing the variables in models:
hr_attr_data['Attrition_ind'] = 0 # new feature or new column
hr_attr_data.loc[ hr_attr_data['Attrition']=='Yes', 'Attrition_ind'] = 1
hr_attr_data.head()? ? ?We level simply create an indicator(13_Loading & Preproces Data from multiple CSV with TF 2_Feature Columns_TF eXtended_num_oov_buckets_Linli522362242的专栏-CSDN博客) or dummy variable that takes on two possible dummy numerical values. For example, based on the gender variable, we can create variable a new variable that takes the form
? ? ?Dummy variables are created for all seven categorical variables (shown here in alphabetical order), which are Business Travel, Department, Education Field, Gender, Job Role, Marital Status, and Overtime. We have ignored four variables from the analysis, as they do not change across the observations, which are Employee count, Employee number, Over18, and Standard Hours:
Business Travel
set( hr_attr_data['BusinessTravel'] )
dummy_businessTravel = pd.get_dummies( hr_attr_data['BusinessTravel'],
prefix = 'busns_trvl'
)
dummy_businessTravel ?
dumpy_dept = pd.get_dummies( hr_attr_data['Department'], prefix='dept' )
dumpy_edufield = pd.get_dummies( hr_attr_data['EducationField'], prefix='edufield' )
dumpy_gender = pd.get_dummies( hr_attr_data['Gender'], prefix='gend' )
dumpy_jobrole = pd.get_dummies( hr_attr_data['JobRole'], prefix='jobrole' )
dumpy_maritstat = pd.get_dummies( hr_attr_data['MaritalStatus'], prefix='maritalstat' )
dumpy_overtime = pd.get_dummies( hr_attr_data['OverTime'], prefix='overtime' )? ? Continuous variables are separated and will be combined with the created dummy variables later:
continuous_columns = ['Age','DailyRate','DistanceFromHome', 'Education',
'EnvironmentSatisfaction','HourlyRate','JobInvolvement',
'JobLevel','JobSatisfaction', 'MonthlyIncome', 'MonthlyRate',
'NumCompaniesWorked','PercentSalaryHike', 'PerformanceRating',
'RelationshipSatisfaction','StockOptionLevel', 'TotalWorkingYears',
'TrainingTimesLastYear','WorkLifeBalance', 'YearsAtCompany',
'YearsInCurrentRole', 'YearsSinceLastPromotion','YearsWithCurrManager'
]
hr_attr_continous = hr_attr_data[continuous_columns]
hr_attr_continous.head()
? ? ?In the following step, both derived dummy variables from categorical variables and straight continuous variables are combined:
hr_attr_data_new = pd.concat( [dummy_businessTravel, dumpy_dept, dumpy_edufield, dumpy_gender,
dumpy_jobrole, dumpy_maritstat, dumpy_overtime,
hr_attr_continous, hr_attr_data['Attrition_ind']
],
axis=1
)
hr_attr_data_new.head()
? ? ?Here, we have not removed one extra derived dummy variable for each categorical variable due to the reason that multi-collinearity does not create a problem in decision trees as it does in either logistic or linear regression, hence we can simply utilize all the derived variables in the rest of the chapter, as all the models utilize decision trees as an underlying model, even after performing ensembles of it.
dummy_businessTravel?: {'Non-Travel', 'Travel_Frequently', 'Travel_Rarely'}
Dummy_businessTravel variable has 3 possible values, in fact we can use 2 bits to represent {'Travel_Frequently': 10,'Travel_Rarely':01, ?'Non-Travel':00}.But, here we use 3 digits, which means that the first digit is redundant {'Travel_Frequently': 010,'Travel_Rarely':001, ?'Non-Travel':000}。 In other words, 'Non-Travel' is a redundant dummy variable
? ? ?Once basic data has been prepared, it needs to be split by 70-30 for training and testing purposes:
# Train and Test split
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split( hr_attr_data_new.drop(['Attrition_ind'], axis=1),
hr_attr_data_new['Attrition_ind'],
train_size=0.7,
random_state=42
)
x_train.shape, x_test.shape, y_train.shape?
Decision tree classifier
? ? ?The DecisionTtreeClassifier from scikit-learn has been utilized for modeling purposes, which is available in the tree submodule:
# Decision Tree Classifier
from sklearn.tree import DecisionTreeClassifier? ? ?The parameters selected for the DT classifier are in the following code with splitting criterion as Gini, Maximum depth as 5, the minimum number of observations required for qualifying split is 2(min_samples_split=2), and the minimum samples that should be present in the terminal node is 1(min_samples_leaf=1):
dt_fit = DecisionTreeClassifier( criterion='gini', max_depth=5, min_samples_split=2,
min_samples_leaf=1, random_state=42
)
dt_fit.fit(x_train, y_train)?
print( "\nDecision Tree - Train Confusion Matrix\n\n",
pd.crosstab( y_train, dt_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)?
- Accuracy = (TP+TN)/(TP+FP+FN+TN) = (844 + 78)/(844+9+98+78) = 0.896
Accuracy answers the following question: How many instances did we correctly label out of all the instances? - Precision = TP/(TP+FP) # True predicted/ (True predicted + False predicted)? = 78/(78+9)=0.896
Precision answers the following: How many of those who we labeled as target class(Attrition)?are actually target class(Attrition=Yes)? - Recall (aka Sensitivity)?= TP/(TP+FN) = 78/(78+98) = 0.443
Recall answers the following question: Of all the instances who are target class(Attrition=Yes), how many of those we correctly predict? - F1 Score = 2*(Recall*Precision) / (Recall+Precision) = 2*(0.443*0.896)/(0.443+0.896)=0.593
F1 Score considers both precision and recall.
from sklearn.metrics import accuracy_score, classification_report
print( '\nDecision Tree - Train accuracy\n\n',
round( accuracy_score( y_train,
dt_fit.predict(x_train)
),
3
)
)?
print( '\nDecision Tree - Train Classification Report\n',
classification_report( y_train,
dt_fit.predict(x_train),
digits=3
)
)Accuracy = (TP+TN)/(TP+FP+FN+TN) = (844 + 78)/(844+9+98+78) = 922/1029 = 0.896
Precision = TP/(TP+FP) # True predicted/ (True predicted + False predicted)? = 78/(78+9)=0.896
Recall (aka Sensitivity)?= TP/(TP+FN) = 78/(78+98) =78/176= 0.443
?
<==
macro avg:?进行简单算术平均 unweighted mean; AllClassesAreEquallyImportant
0.896 = (0.896+0.897)/2 ? ?0.716=(0.989+0.443)/2 ? ?0.767= (0.940+0.593)/2
Note: 2 since there exist 2 possible values(0,1)
weighted avg: (start from left bottom)
0.896=(0.896*853 +0.897*176)/(853+176) ?: 853,176 are weights or supports
0.896=(0.989*853 +0.443*176)/(853+176)
0.881=(0.940*853 +0.593*176)/(853+176)
03_Classification_2_regex_confusion matrix_.reshape([-1])_score(average=“macro“)_interpolation.shift_Linli522362242的专栏-CSDN博客
print( "\nDecision Tree - Test Confusion Matrix\n\n",
pd.crosstab( y_test, dt_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nDecision Tree - Test accuracy\n\n',
round( accuracy_score( y_test,
dt_fit.predict(x_test)
),
3
)
)?
print( '\nDecision Tree - Test Classification Report\n',
classification_report( y_test,
dt_fit.predict(x_test),
digits=3
)
)?
? ? ?By carefully observing the results, we can infer that, even though the test accuracy is high (84.6%), the precision and recall of one category (Attrition = Yes) is low (precision = 0.39 and recall = 0.20). This could be a serious issue when management tries to use this model to provide some extra benefits proactively[?pro???kt?vli]主动地 to the employees with a high chance of attrition prior to actual attrition, as this model is unable to identify the real employees who will be leaving. Hence, we need to look for other modifications; one way is to control the model by using class weights. By utilizing class weights, we can increase the importance of a particular class at the cost of an increase in other errors.
? ? ?For example, by increasing class weight to category 1(Attrition = Yes, we care), we can identify more employees with the characteristics of actual attrition, but by doing so, we will mark some of the nonpotential churner employees as potential attriters (which should be acceptable).
例如，通过将类权重增加到类别 1，我们可以识别出更多具有实际流失特征的员工，但这样做，我们会将一些非潜在流失员工标记为潜在流失员工（这应该是可以接受的）。
churner
? ? ?Another classic example of the important use of class weights is, in banking scenarios. When giving loans, it is better to reject some good applications than accepting bad loans与其接受不良贷款，不如拒绝一些好的申请. Hence, even in this case, it is a better idea to use higher weight to defaulters over nondefaulters:(My understanding: because applicants with good applications have bad credit records, they are rejected. But applicants for non-performing loans have good credit records)
Tuning class weights in decision tree classifier
? ? ?In the following code, class weights are tuned to see the performance change in decision trees with the same parameters. A dummy DataFrame is created to save all the results of various precision-recall details of combinations:
dummyarray = np.empty( (6,10) )
dt_wttune = pd.DataFrame( dummyarray )? ? Metrics to be considered for capture are weight for zero and one category (for example, if the weight for zero category given is 0.2, then automatically, weight for the one should be 0.8, as total weight should be equal to 1), training and testing accuracy, precision for zero category, one category, and overall. Similarly, recall for zero category, one category, and overall are also calculated:
dt_wttune.columns = ['zero_wght', 'one_wght', # weight for zero and one category
'tr_accuracy', 'tst_accuracy', # training and testing accuracy
'prec_zero', 'prec_one', 'prec_ovll', # precision
'recl_zero', 'recl_one', 'recl_ovll' # recall
]? ? ?Weights for the zero category are verified from 0.01 to 0.5, as we know we do not want to explore cases where the zero category will be given higher weightage than one category:
#######################
classification_report( y_test,
dt_fit.predict(x_test),
digits=3
).split()
#######################
zero_clwghts = [0.01, 0.1, 0.2, 0.3, 0.4, 0.5]
for i in range( len(zero_clwghts) ):
clwght = { 0:zero_clwghts[i],
1:1.0-zero_clwghts[i]
}
dt_fit = DecisionTreeClassifier( criterion='gini', max_depth=5, min_samples_split=2,
min_samples_leaf=1, random_state=42,
class_weight=clwght )######
dt_fit.fit( x_train, y_train )
dt_wttune.loc[i, 'zero_wght'] = clwght[0]
dt_wttune.loc[i, 'one_wght'] = clwght[1]
dt_wttune.loc[i, 'tr_accuracy'] = round( accuracy_score( y_train, dt_fit.predict(x_train) ),
3
)
dt_wttune.loc[i, 'tst_accuracy'] = round( accuracy_score( y_test, dt_fit.predict(x_test) ),
3
)
clf_sp = classification_report( y_test, dt_fit.predict( x_test) ).split()
dt_wttune.loc[i, 'prec_zero'] = float( clf_sp[5] ) # ['0', 'precision']
dt_wttune.loc[i, 'prec_one'] = float( clf_sp[10] ) # ['1', 'precision']
dt_wttune.loc[i, 'prec_ovll'] = float( clf_sp[19]) # ['macro avg','precision']
dt_wttune.loc[i, 'recl_zero'] = float( clf_sp[6] ) # [0, 'recall']
dt_wttune.loc[i, 'recl_one'] = float( clf_sp[11] ) # [1, 'recall']
dt_wttune.loc[i, 'recl_ovll'] = float( clf_sp[20] )# ['macro avg','recall']
print( '\nClass Weights', clwght,
'Train accuracy:', round( accuracy_score( y_train,
dt_fit.predict(x_train)
),
3
),
'Test accuracy:', round( accuracy_score( y_test,
dt_fit.predict(x_test)
),
3
)
)
print( 'Test Confusion Matrix\n\n', pd.crosstab( y_test, dt_fit.predict( x_test ),
rownames = ['Actuall'],
colnames = ['Predicted']
)
)?
? ? ?From the preceding screenshot, we can see that at class weight values of 0.3 (for zero) and 0.7 (for one) it is identifying a higher number of attriters (24 out of 61=37+24, Recall (aka Sensitivity)=TP/(TP+FN) , Recall answers the following: Of all the instances who are target class(Attrition=Yes), how many of those we correctly predict?) without compromising 妥协，让步； 损害test accuracy 83.7%(higher) using decision trees methodology:?
Hidden:?First consider the high accuracy rate, and then consider the high recall
?
dt_wttune
Bagging classifier
? ? ?As we have discussed already, decision trees suffer from high variance, which means if we split the training data into two random parts separately and fit two decision trees for each sample, the rules obtained would be very different. Whereas low variance and high bias models, such as linear or logistic regression, will produce similar results across both samples. Bagging refers to bootstrap aggregation (repeated sampling with replacement and perform aggregation of results to be precise), which is a general purpose methodology to reduce the variance of models. In this case, they are decision trees.
? ? ?Aggregation reduces the variance, for example, when we have n independent observations
each with variance 
and the variance of the mean x? of the observations is given by 
, which illustrates by averaging a set of observations that it reduces variance. Here, we are reducing variance by taking many samples from training data (also known as bootstrapping), building a separate decision tree on each sample separately, averaging the predictions for regression, and calculating mode for classification problems in order to obtain a single low-variance model that will have both low bias and low variance:?
? ? ?In a bagging procedure, rows are sampled while selecting all the columns/variables (whereas, in a random forest, both rows and columns would be sampled, which we will cover in the next section) and fitting individual trees for each sample. In the following diagram, two colors (pink and blue) represent two samples, and for each sample, a few rows are sampled, but all the columns (variables) are selected every time. One issue that exists due to the selection of all columns is that most of the trees will describe the same story, in which the most important variable will appear initially in the split, and this repeats in all the trees, which will not produce decorrelated trees, so we may not get better performance when applying variance reduction. This issue will be avoided in random forest (we will cover this in the next section of the chapter), in which we will sample both rows and columns as well:
? ? ?In the following code, the same HR data has been used to fit the bagging classifier in order to compare the results apple to apple with respect to decision trees:
# Bagging Classifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier? ? ?The base classifier used here is Decision Trees with the same parameter setting that we used in the decision tree example:
? ? ?Parameters used in bagging are,
- n_estimators to represent the number of individual decision trees used as 5,000,
- max_samples(The number of samples to draw from X to train each base estimator (with replacement by default, see?
bootstrap?for more details).) and - max_features(The number of features to draw from X to train each base estimator (without replacement by default, see?
bootstrap_features?for more details).) - selected are 0.67 and 1.0 respectively, which means it will select
of observations for each tree and all the features. For further details, please refer to the scikit-learn manual sklearn.ensemble.BaggingClassifier — scikit-learn 0.24.2 documentation: bag_fit = BaggingClassifier( base_estimator=dt_fit, n_estimators=5000, max_samples=0.67, max_features=1.0, bootstrap=True, # with replacement, There may be duplication in 67% of the samples for each tree bootstrap_features=False, # without replacement n_jobs=-1, #(–1 tells Scikit-Learn to use all available CPU cores random_state=42 ) bag_fit.fit( x_train, y_train )print( "\nBagging - Train Confusion Matrix\n\n", pd.crosstab( y_train, bag_fit.predict(x_train), rownames=["Actuall"], colnames=["Predicted"] ) ) print( "\nBagging - Train accuracy", round( accuracy_score( y_train, bag_fit.predict(x_train) ), 3 ) ) print( "\nBagging - Train Classification Report\n", classification_report( y_train, bag_fit.predict(x_train), digits=3 ) ) print( "\nBagging - Test Confusion Matrix\n\n", pd.crosstab( y_test, bag_fit.predict(x_test), rownames=["Actuall"], colnames=["Predicted"] ) ) print( "\nBagging - Test accuracy", round( accuracy_score( y_test, bag_fit.predict(x_test) ), 3 ) ) print( "\nBagging - Test Classification Report\n", classification_report( y_test, bag_fit.predict(x_test), digits=3 ) )
?
? ? ?After analyzing the results from bagging, the test accuracy obtained was 87.1%, whereas for decision tree it was 84.6%(class_weight=None, If None, all classes are supposed to have weight 1) OR?0.837(class_weight={0:0.3, 1:0.7}).
Comparing the number of actual attrited employees identified, there were 13 in bagging, whereas in decision tree there were 12(class_weight=None) OR 24(class_weight={0:0.3, 1:0.7}),
but the number of 0 classified as 1 significantly reduced to 8 (FP) compared with 19 in DT(class_weight=None) OR 35(class_weight={0:0.3, 1:0.7}).
bagging, DT(class_weight=None),?DT(class_weight={0:0.3, 1:0.7}),
,??
,? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Overall, bagging improves performance over the single tree.
Random forest classifier
? ? ?Random forests provide an improvement over bagging by doing a small tweak that utilizes decorrelated trees. In bagging, we build a number of decision trees on bootstrapped samples from training data, but the one big drawback with the bagging technique is that it selects all the feature variables. By doing so, in each decision tree, the order of candidate/variable chosen to split remains more or less the same for all the individual trees, which look correlated with each other. Variance reduction on correlated individual entities does not work effectively while aggregating them.
? ? ?In random forest, during bootstrapping (repeated sampling with replacement), samples were drawn from training data; not just simply the second and third observations randomly selected, similar to bagging, but it also selects the few predictors/columns out of all predictors (m predictors out of total p predictors).
? ? ?The thumb rule经验法则 for variable selection of m variables out of total variables p is m = sqrt(p) for classification and m = p/3 for regression problems randomly to avoid correlation among the individual trees. By doing so, significant improvement in the accuracy can be achieved. This ability of RF makes it one of the favorite algorithms used by the data science community, as a winning recipe across various competitions or even for solving practical problems in various industries.
? ? ?In the following diagram, different colors represent different bootstrap samples. In the first
sample, the 1st, 3rd, 4th, and 7th columns are selected, whereas, in the second bootstrap sample, the 2nd, 3rd, 4th, and 5th columns are selected respectively. In this way, any columns can be selected at random, whether they are adjacent to each other or not. Though the thumb rules of sqrt (p) or p/3 are given, readers are encouraged to tune the number of predictors to be selected:
? ? ?The sample plot shows the impact of a test error change while changing the parameters selected, and it is apparent that a m = sqrt(p) scenario gives better performance on test data compared with m =p (we can call this scenario bagging):
? ? ?Random forest classifier has been utilized from the scikit-learn package here for illustration purposes:
# Random Forest Classifier
from sklearn.ensemble import RandomForestClassifier? ? ?The parameters used in random forest are: n_estimators representing the number of individual decision trees used is 5000, maximum features(max_features) selected are auto, which means it will select sqrt(p) for classification and p/3 for regression automatically. Here is the straightforward classification problem though. Minimum samples per leaf(min_samples_leaf) provide the minimum number of observations required in the terminal node:
? ? ?The number of features to consider when looking for the best split:
-
If int, then consider?
max_features?features at each split. -
If float, then?
max_features?is a fraction and?round(max_features?*?n_features)?features are considered at each split. -
If “auto”, then?
max_features=sqrt(n_features). -
If “sqrt”, then?
max_features=sqrt(n_features)?(same as “auto”). -
If “log2”, then?
max_features=log2(n_features). -
If None, then?
max_features=n_features.
rf_fit = RandomForestClassifier( n_estimators=5000, criterion='gini', max_depth=5,
min_samples_split=2, bootstrap=True, max_features='auto',
random_state=42, min_samples_leaf=1, class_weight={0:0.3, 1:0.7}
)
rf_fit.fit( x_train, y_train )print( '\nRandom Forest - Train Confusion Matrix\n\n',
pd.crosstab( y_train, rf_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nRandom Forest - Train accuracy',
round( accuracy_score( y_train, rf_fit.predict(x_train) ), 3)
)
print( '\nRandom Forest - Train Classification Report\n',
classification_report( y_train, rf_fit.predict(x_train) )
)?
print( '\nRandom Forest - Test Confusion Matrix\n\n',
pd.crosstab( y_test, rf_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nRandom Forest - Test accuracy',
round( accuracy_score( y_test, rf_fit.predict(x_test) ), 3)
)
print( '\nRandom Forest - Test Classification Report\n',
classification_report( y_test, rf_fit.predict(x_test) )
)?
? ? ?Random forest classifier produced 87.8% test accuracy compared with bagging 87.1%, and also identifies 14 actually attrited employees in contrast with bagging, for which 12 attrited employees have been identified:
x_train.columns?
# Plot of Variable importance by mean decrease in gini
model_ranks = pd.Series( rf_fit.feature_importances_,
index=x_train.columns,
name='Importance', # descending
).sort_values( ascending=False, inplace=False )
model_ranks.index.name = 'Variables'
top_features = model_ranks.iloc[:31].sort_values( ascending=True, inplace=False )rf_fit.feature_importances_
model_ranks[:31]?
import matplotlib.pyplot as plt
plt.figure( figsize=(20,10) )
ax = top_features.plot( kind='barh' )
ax.set_title( 'Variable Importance Plot from RF', fontsize=20 )
ax.set_xlabel( 'Mean decrease in Variance', fontsize=14 )
ax.yaxis.label.set_size(14)
_ = ax.set_yticklabels( top_features.index, fontsize=14 )
? ? ?From the variable importance plot, it seems that the monthly income variable seems to be most significant, followed by overtime, total working years, stock option levels, years at company, and so on. This provides us with some insight into what are major contributing factors that determine whether the employee will remain with the company or leave the organization:
Random forest classifier - grid search
? ? ?Tuning parameters in a machine learning model play a critical role. Here, we are showing a grid search example on how to tune a random forest model:
# Random Forest Classifier - Grid Search
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV
pipeline = Pipeline([
('clf',
RandomForestClassifier( criterion='gini',
class_weight = {0:0.3, 1:0.7},
random_state=42, # random_state=None,
) # the result of each run will be different
)
])? ? ?Tuning parameters are similar to random forest parameters apart from verifying all the combinations using the pipeline function. The number of combinations to be evaluated will be (3 x 3 x 2 x 2) *5 =36*5 = 180 combinations. Here 5 is used in the end, due to the crossvalidation of five-fold:
parameters = {
'clf__n_estimators':(2000,3000,5000),
'clf__max_depth':(5,15,30),
'clf__min_samples_split':(2,3),
'clf__min_samples_leaf':(1,2)
} # (3 x 3 x 2 x 2) * 5 = 180 combinations
grid_search = GridSearchCV( pipeline, parameters, n_jobs=-1, cv=5, verbose=3, scoring='accuracy' )
grid_search.fit( x_train, y_train )
print( 'Best Training score: %0.3f' % grid_search.best_score_ )
print( 'Best parameters set:' )
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted( parameters.keys() ):
print( '\t%s: %r' % (param_name, best_parameters[param_name] ) )?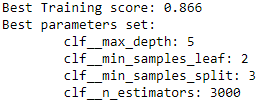
VS
Reason:?random_state=None
Since the parameter values in the running results of the two computers are different, but clf__n_estimators=3000, I use the combination to lock all the parameter combinations of clf__n_estimators=3000
predictions = grid_search.predict( x_test )
print( 'Testing accuracy:', round( accuracy_score(y_test, predictions),
4
)
)
print( '\nComplete report of Testing data\n',
classification_report(y_test, predictions)
)
print( '\n\nRandom Forest Grid Search- Test Confusion Matrix\n\n',
pd.crosstab( y_test, predictions, rownames=['Actual'], colnames=['Predected'] )
)
?#################################combination
? ? ?Since the parameter values in the running results of the two computers are different, but clf__n_estimators=3000, I use the combination to lock all the parameter combinations of clf__n_estimators=3000
? ? ?I divided the parameters into 3 parts, and then ran them on 3 machines, the following is the code of the middle part
import itertools as it
parameters = {
'clf__n_estimators':(2000,3000,5000),
'clf__max_depth':(5,15,30),
'clf__min_samples_split':(2,3),
'clf__min_samples_leaf':(1,2)
}
combinations = [ { param_key:[param_val] for (param_key, param_val) in zip( parameters.keys(),peram_val ) }
for peram_val in it.product( *( parameters[peram_key]
for peram_key in parameters.keys()
)
)
]
combinations[12:24] # 3 x 3 x 2 x 2=36 / 3=12
grid_search = GridSearchCV( pipeline, combinations[12:24], n_jobs=-1, cv=5, verbose=3, scoring='accuracy' )
grid_search.fit( x_train, y_train )
print( 'Best Training score: %0.3f' % grid_search.best_score_ )
print( 'Best parameters set:' )
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted( parameters.keys() ):
print( '\t%s: %r' % (param_name, best_parameters[param_name] ) )
predictions = grid_search.predict( x_test )
print( 'Testing accuracy:', round( accuracy_score(y_test, predictions),
4
)
)
print( '\nComplete report of Testing data\n',
classification_report(y_test, predictions)
)
print( '\n\nRandom Forest Grid Search- Test Confusion Matrix\n\n',
pd.crosstab( y_test, predictions, rownames=['Actual'], colnames=['Predected'] )
) 
vs
?Reason:?random_state=None
#################################
? ? ? In the preceding results, grid search seems to not provide many advantages compared with
the already explored random forest result. But, practically, most of the times, it will provide
better and more robust results compared with a simple exploration of models. However, by carefully evaluating many different combinations, it will eventually discover the best
parameters combination.
AdaBoost classifier
? ? ?Boosting is another state-of-the-art model that is being used by many data scientists to win so many competitions. In this section, we will be covering the AdaBoost algorithm followed by gradient boost and extreme gradient boost (XGBoost). Boosting is a general approach that can be applied to many statistical models. However, we will be discussing the application of boosting in the context of decision trees. In bagging, we have taken multiple samples from the training data and then combined the results of individual trees to create a single predictive model; this method runs in parallel, as each bootstrap sample does not depend on others. Boosting works in a sequential manner and does not involve bootstrap sampling; instead, each tree is fitted on a modified version of an original dataset and finally added up to create a strong classifier:
? ? ?The preceding figure is the sample methodology on how AdaBoost works. We will cover step-by-step procedures in detail in the following algorithm description. Initially, a simple classifier has been fitted on the data (also called a decision stump, which splits the data into just two regions) and whatever the classes correctly classified will be given less weightage in the next iteration (iteration 2) and higher weightage for misclassified classes (observer + blue icons), and again another decision stump/weak classifier will be fitted on the data and will change the weights again for the next iteration (iteration 3, here check the - symbols for which weight has been increased). Once it finishes the iterations, these are combined with weights (weights automatically calculated for each classifier at each iteration based on error rate) to come up with a strong classifier, which predicts the classes with surprising accuracy.
Algorithm for AdaBoost consists of the following steps:
1. Initialize the observation weights 
= 1/N, i=1, 2, …, N. Where N = Number of observations.
? ? OR?Set the weight vector,?W, to?uniform weights, where
= 1 .
2. For m = 1 to M boosting rounds:?
- Fit a classifier Gm(x) to the training data using weights
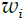
OR?Train a weighted weak learner:?
?= train(𝑿,?𝒚,?W) . - Compute:
? ? ? ? ? ? ? ?
? ? ? ? OR- b. Predict class labels:?
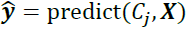??and j=m - c. Compute weighted error rate:?𝜀?= W?? (𝒚? ≠ 𝒚)?,?
the dot-product between?two vectors by a dot symbol?(?? ),? Note: (𝒚? ≠ 𝒚)? refers to a binary vector consisting of 1s and 0s, where a 1 is assigned if the prediction is incorrect and 0 is assigned otherwise.
- b. Predict class labels:?
-
Compute:?
? ? ? ? ? ? ? ??
?
? ? ? ? ? ? ? ??OR
? ? ? ? ? ? ? ??d.?
and j=m and 0.5 is learning rate -
Set:
? ? ??
? ? ? OR?-
e. Update weights:?
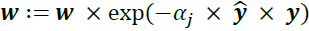?and the?element-wise multiplication?by the cross symbol ( × )? -
f. Normalize weights to sum to 1:?
-
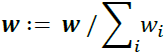
3. Output:
? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? ?OR
? ? ? ? ? ? ? ? ?𝒚? =?
? ? ?In bagging and random forest algorithms, we deal with the columns of the data; whereas, in boosting, we adjust the weights of each observation and don't elect a few columns.
? ? ?Although the AdaBoost algorithm seems to be pretty straightforward, let's walk through a more concrete example using a training dataset consisting of 10 training examples, as illustrated in the following table:
1. The first column of the table depicts the indices of training examples 1 to 10.
2. In the second column, you can see the feature values of the individual samples, assuming this is a one-dimensional dataset.
3. The third column shows the true class label, 
, for each training sample, 
?, where 
?∈ {1, ?1} .
4. The initial weights are shown in the fourth column; we initialize the weights uniformly (assigning the same constant value) and normalize them to sum to 1. In the case of the 10-sample training dataset, we therefore assign 0.1 to each weight, 
, in the weight vector, W.
5. The predicted class labels, 𝒚? , are shown in the fifth column, assuming that our splitting criterion is 𝑥 ≤ 3.0 .
6. The last column of the table then shows the updated weights based on the update rules that we defined in the pseudo code.
? ? ?Since the computation of the weight updates may look a little bit complicated at first, we will now follow the calculation step by step. We will start by computing the weighted error rate, 𝜀 , as described in step 2.c:(𝜀 = 𝒘 ? (𝒚? ≠ 𝒚))
? 𝜀 = 𝒘 ? (𝒚? ≠ 𝒚), 1 is assigned if the prediction is incorrect and 0 is assigned otherwise
? ? ?Next, we will compute the coefficient, 
— shown in step 2.d(??)—which will later be used in step 2.e?(
) to update the weights, as well as for the weights in the majority vote prediction (step 3):
??? ?After we have computed the coefficient,??, we can now update the weight vector using the following equation (step?2e):?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Here, 𝒚? × 𝒚 is an element-wise multiplication between the vectors of the predicted and true class labels, respectively. Thus, if a prediction, 
, is correct, 
?will have a positive sign so that we decrease the ith weight, since ?is a positive number as well:?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Similarly, we will increase the ith weight?if??predicted the label incorrectly, like this:?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Alternatively, it's like this:?
?After we have?updated each weight?in the weight vector, we?normalize the weights?so that they sum up to 1?(step 2.f ):?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Here,?
= 7 × 0.065 + 3 × 0.153 = 0.914 .
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Thus, each weight that corresponds to a correctly classified example will be reduced from the initial value of 0.1 to 0.065/0.914 ≈ 0.071 for the next round of boosting. Similarly, the weights of the incorrectly classified examples will increase from 0.1 to 0.153/0.914 ≈ 0.167.
? ? ?We fit a classifier on the data and evaluate overall errors. The error used for calculating weight should be given for that classifier in the final additive model (α) evaluation. The intuitive sense is that the higher weight will be given for the model with fewer errors. Finally, weights for each observation will be updated. Here, weight will be increased for incorrectly classified observations in order to give more focus to the next iterations, and weights will be reduced for correctly classified observations.
? ? ?All the weak classifiers are combined with their respective weights to form a strong classifier. In the following figure, a quick idea is shared on how weights changed in the last iteration compared with the initial iteration:
# Adaboost Classifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier? ? ?Decision stump is used as a base classifier for AdaBoost. If we observe the following code, the depth of the tree remains as 1, which has decision taking ability only once (also considered a weak classifier):
dtree = DecisionTreeClassifier( criterion='gini', max_depth=1 )? ? ?In AdaBoost, decision stump has been used as a base estimator to fit on whole datasets and
then fits additional copies of the classifier on the same dataset up to 5000 times(n_estimators=5000). The learning rate shrinks the contribution of each classifier by 0.05(learning_rate=0.05). There is a trade-off between the learning rate and number of estimators. By carefully choosing a low learning rate and a long number of estimators, one can converge optimum very much, however at the expense of computing power:
adabst_fit = AdaBoostClassifier( base_estimator=dtree, n_estimators=5000,
learning_rate=0.05,
algorithm='SAMME.R',
random_state=42
)
adabst_fit.fit( x_train, y_train )algorithm：这个参数只有AdaBoostClassifier有。主要原因是scikit-learn实现了两种Adaboost分类算法，SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量，SAMME使用了和我们的原理篇里二元分类Adaboost算法的扩展，即用对样本集(Ensemble)分类效果作为弱学习器(weak learner)权重，而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值，迭代一般比SAMME快，因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了，但是要注意的是使用了SAMME.R， 则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。?
learning_rate
<==
<==
（这个是一般的权重更新）:?AdaBoostClassifier和AdaBoostRegressor权重更新(0.5 is learning rate)==>==>normalize==>𝒚? =OR 都有learning_rate，即每个弱学习器的权重缩减系数
，在原理篇的正则化章节我们也讲到了，加上了正则化项，我们的强学习器的迭代公式为
。
的取值范围为0<
≤1。对于同样的训练集拟合效果，较小的
意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。所以这两个参数n_estimators和learning_rate要一起调参。一般来说，可以从一个小一点的
开始调参，默认是1.
sklearn.ensemble.AdaBoostRegressor
loss：这个参数只有AdaBoostRegressor有，Adaboost.R2算法需要用到。有线性‘linear’, 平方‘square’和指数 ‘exponential’三种选择, 默认是线性，一般使用线性就足够了，除非你怀疑这个参数导致拟合程度不好。这个值的意义在原理篇我们也讲到了，它对应了我们对第k个弱分类器的中第i个样本的误差的处理，即：如果是线性误差，则
；如果是平方误差，则
，如果是指数误差，则
，Ek为训练集上的最大误差
?
print( '\nAdaBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, adabst_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nAdaBoost - Train accuracy',
round( accuracy_score( y_train, adabst_fit.predict(x_train) ), 3)
)
print( '\nAdaBoost - Train Classification Report\n',
classification_report( y_train, adabst_fit.predict(x_train) )
)?
print( '\nAdaBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, adabst_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nAdaBoost - Test accuracy',
round( accuracy_score( y_test, adabst_fit.predict(x_test) ), 3)
)
print( '\nAdaBoost - Test Classification Report\n',
classification_report( y_test, adabst_fit.predict(x_test) )
)?
? ? ?The result of the AdaBoost seems to be much better than the known best random forest classifiers in terms of the recall of 1 value(0.38 vs random forest?recall rate=0.23). Though there is a slight decrease in accuracy to 86.8% compared with the best accuracy of 87.8%, the number of 1's predicted is 23 from the AdaBoost, which is 15 with some expense of an increase in 0's, but it really made good progress in terms of identifying actual attriters.
Gradient boosting classifier
? ? ?Gradient boosting is one of the competition-winning algorithms that work on the principle of boosting weak learners iteratively by shifting focus towards problematic observations that were difficult to predict in previous iterations and performing an ensemble of weak learners, typically decision trees. It builds the model in a stage-wise fashion as other boosting methods do, but it generalizes them by allowing optimization of an arbitrary differentiable loss function.
? ? ?Let's start understanding Gradient Boosting with a simple example, as GB challenges many data scientists in terms of understanding the working principle:
- 1. Initially, we fit the model on observations producing 75% accuracy and the remaining unexplained variance is captured in the error term:
- 2. Then we will fit another model on the error term to pull the extra explanatory component and add it to the original model, which should improve the overall accuracy:
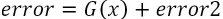
similar to?
- 3. Now, the model is providing 80% accuracy and the equation looks as follows:
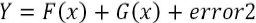
- 4. We continue this method one more time to fit a model on the error2 component to extract a further explanatory component:
- 5. Now, model accuracy is further improved to 85% and the final model equation looks as follows:
- 6. Here, if we use weighted average (higher importance given to better models that
predict results with greater accuracy than others) rather than simple addition, it
will improve the results further. In fact, this is what the gradient boosting
algorithm does!
? ? After incorporating weights, the name of the error changed from error3 to error4, as both errors may not be exactly the same. If we find better weights, we will probably get an accuracy of 90% instead of simple addition, where we have only got 85%.
Gradient boosting involves three elements:
- Loss function to be optimized: Loss function depends on the type of problem being solved. In the case of
- regression problems, mean squared error is used, and in
- classification problems, the logarithmic loss will be used. In boosting, at each stage, unexplained loss from prior iterations will be optimized rather than starting from scratch.
- Weak learner to make predictions: Decision trees are used as a weak learner in gradient boosting.
- Additive model to add weak learners to minimize the loss function: Trees are added one at a time and existing trees in the model are not changed. The gradient descent procedure is used to minimize the loss when adding trees.
The algorithm for Gradient boosting consists of the following steps:
输出是强学习器f(x)?梯度提升树(GBDT)原理小结 - 刘建平Pinard - 博客园
- 1. Initialize model with a constant value(使损失函数极小化的常数值):
a constant function
OR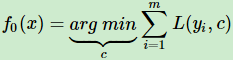
Initializes the constant optimal constant model, which is just a single terminal node that will be utilized as a starting point to tune it further in the next steps - 2. For Iteration m = 1 to M（从区域/树1 到 区域/树M，逐渐划分disjoint regions）:
- a) For each sample from index i = 1, 2, …, N compute:?计算负梯度
calculates the (so-called pseudo-residuals伪残差)residuals/errors
by comparing actual outcome
with predicted results
计算损失函数的负梯度在当前模型的值，将它作为残差的估计，followed by (2b and 2c) in which the next decision tree will be fitted on error terms to bring in more explanatory power to the model(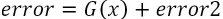==>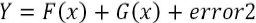), - b) （Many attempts）Fit a regression tree to the targets
?==>giving terminal regions(叶子区域m)?
,
j = 1, 2, …,
,?其中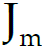为回归区域/树m的叶子节点的个数。 - c) For?terminal regions(叶子区域m) j = 1, 2, …, 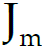, compute计算最佳拟合值（找到了最佳划分位置m）:
- d) Update 更新强学习器:
https://en.wikipedia.org/wiki/Gradient_boosting
add the extra component to the model at last iteration
- a) For each sample from index i = 1, 2, …, N compute:?计算负梯度
- Output:
ensemble all weak learners to create a strong learner.（类似于AdaBoost (Adaptive Boosting适应性提升)
）
?? ? ?Gradient boosting is a machine learning technique for regression and classification problems, which produces a prediction model in the form of an ensemble of weak?prediction models, typically decision trees.?(Wikipedia definition)
? ? ?The objective of any supervised learning algorithm is to define a loss function and minimize it. Let’s see how maths work out for Gradient Boosting algorithm. Say we have mean squared error (MSE) as loss defined as:
?? ? ?We want our predictions, such that our loss function (MSE) is minimum. By using?gradient descent( Note, we usually use gradient descent to?update each sample feature coefficents or feature weights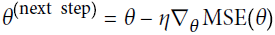
?then?
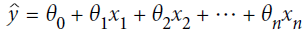, But here is different, after we got the predicted value,?we?use gradient descent method to adjust the learning rate (also called step size) according to the following?formula?
?for making?all?predicted values are sufficiently close to actual values?集成学习之Boosting —— Gradient Boosting原理 - massquantity - 博客园
)?and updating our predictions based on a learning rate, we can find the values where MSE is minimum.
##############################https://en.wikipedia.org/wiki/Gradient_boosting
? ? ?Generic gradient boosting at the m-th step would fit a decision tree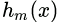 
?to pseudo-residuals. Let 
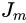?be the number of its leaves. The tree partitions the input space
into 
?disjoint regions and predicts a constant value in each region. Using the indicator notation, the output of 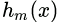?for input x can be written as the sum:
where?
is the value predicted in the region
? ? Then the coefficients ?are multiplied by some value
, chosen using line search so as to minimize the loss function, and the model is updated as follows:
OR
?==>
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? VS?
? ? ? Friedman proposes to modify this algorithm so that it chooses a separate optimal value??for each of the tree's regions, instead of a single?for the whole tree. He calls the modified algorithm "TreeBoost". The coefficients??from the tree-fitting procedure can be then simply discarded and the model update rule becomes:
OR
##############################https://blog.csdn.net/Linli522362242/article/details/105046444
Note: the residual errors 
made by the previous predictor(e.g. classifiers)
? ? ?So, we are basically updating the predictions such that the sum of our residuals is close to 0 (or minimum) and predicted values are sufficiently close to actual values.
? ? ?Let's go through a simple regression example using Decision Trees as the base predictors (of course Gradient Boosting also works great with regression tasks). This is called Gradient Tree Boosting, or Gradient Boosted Regression Trees (GBRT).
First, let's fit a DecisionTreeRegressor to the training set (for example, a noisy quadratic training set):
np.random.seed(42)
X = np.random.rand(100,1) - 0.5
y = 3*X[:,0]**2 + 0.05*np.random.randn(100)
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X,y)
Now train a second DecisionTreeRegressor on the residual errors made by the first predictor:
y2 = y-tree_reg1.predict(X) #residual errors
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X,y2) #y-tree_reg1.predict(X)
Then we train a third regressor on the residual errors made by the second predictor:
y3 = y2-tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X,y3)
Now we have an ensemble containing three trees. It can make predictions on a new instance simply by adding up the predictions of all the trees:
?Here, if we use weighted average (higher importance given to better models that
predict results with greater accuracy than others) rather than simple addition, it
will improve the results further. In fact, this is what the gradient boosting
algorithm does!
X_new = np.array([[0.8]])
y_pred = sum( tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3) )
y_pred
def plot_predictions(regressors, X,y, axes, label=None, style="r-", data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum( regressor.predict( x1.reshape(-1,1) ) for regressor in regressors )
plt.plot( X[:,0], y, data_style, label=data_label ) # plotting data points
plt.plot( x1, y_pred, style, linewidth=2, label=label ) # plotting decision boundaries
if label or data_label:
plt.legend( loc="upper center", fontsize=16 )
plt.axis(axes)plt.figure( figsize=(13,13) )
plt.subplot(321)
plot_predictions( [tree_reg1], X,y, axes=[ -0.5,0.5, -0.1,0.8 ], label="$h_1(x_1)$", style="g-",
data_label="Training set")
plt.ylabel( "$y$", fontsize=16, rotation=0 )#IndexError: string index out of range: plt.ylabel("$y_$", fontsize=16, rotation=0)
plt.title( "Residuals and tree predictions", fontsize=16 )
plt.subplot(322)
plot_predictions( [tree_reg1], X,y, axes=[ -0.5,0.5, -0.1,0.8 ], label="$h(x_1)=h_1(x_1)$",
data_label="Training set")
plt.ylabel("y^ ", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(323)
plot_predictions( [tree_reg2], X,y2, axes=[ -0.5,0.5, -0.5,0.5 ], label="$h_2(x_1)$", style="g-",
data_label="Residuals", data_style="k+") #y2 = y-tree_reg1.predict(X) #residual errors
plt.ylabel("$y-h_1(x_1)$", fontsize=16, rotation=0)
plt.subplot(324)
plot_predictions( [tree_reg1,tree_reg2], X,y, axes=[ -0.5,0.5, -0.1,0.8 ], label="$h(x_1)=h_1(x_1)+h_2(x_1)$")
plt.ylabel("y^ ", fontsize=16, rotation=0)
plt.subplot(325)
plot_predictions( [tree_reg3], X,y3, axes=[-0.5,0.5, -0.5,0.5], label="$h_3(x_1)$", style="g-",
data_label="$y-h_1(x_1)-h_2(x_1)$", data_style="k+") #y3 = y-tree_reg2.predict(X)
plt.ylabel("$y-h_1(x_1)-h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(326)
plot_predictions( [tree_reg1, tree_reg2, tree_reg3], X,y, axes=[-0.5,0.5, -0.1,0.8],
label="$h(x_1)=h_1(x_1)+h_2(x_1)+h_3(x_1)$" )
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("y^", fontsize=16, rotation=0)
plt.subplots_adjust(left=0.1, right=0.9, wspace=0.25)
plt.show()
Figure 7-9. Gradient Boosting
?? ? ?Figure 7-9 represents the predictions of these three trees in the left column, and the ensemble's predictions in the right column. In the first row, the ensemble has just one tree, so its predictions are exactly the same as the first tree's predictions. In the second row, a new tree is trained on the residual errors of the first tree. On the right you can see that the ensemble's predictions are equal to the sum of the predictions of the first two trees. Similarly, in the third row another tree is trained on the residual errors of the second tree. You can see that the ensemble's predictions gradually get better as trees are added to the ensemble.
Comparison between AdaBoosting versus gradient boosting
? ? ?After understanding both AdaBoost and gradient boost, readers may be curious to see the differences in detail. Here, we are presenting exactly that to quench your thirst!
? ? ?The gradient boosting classifier from the scikit-learn package has been used for computation here:
# Gradientboost Classifier
from sklearn.ensemble import GradientBoostingClassifier? ? ? Parameters used in the gradient boosting algorithms are as follows. Deviance has been used
for loss, as the problem we are trying to solve is 0/1 binary classification. The learning rate
has been chosen as 0.05(learning_rate=0.05), number of trees to build is 5000 trees(n_estimators=5000), minimum sample per leaf/terminal node is 1(min_samples_leaf=1), and minimum samples needed in a bucket for qualification for splitting is 2(min_samples_split=2):
loss{‘deviance’, ‘exponential’}, default=’deviance’
The loss function to be optimized. ‘deviance’ refers to deviance (= logistic regression) for classification with probabilistic outputs. For loss ‘exponential’ gradient boosting recovers the AdaBoost algorithm.
gbc_fit = GradientBoostingClassifier( loss='deviance',
learning_rate=0.05, n_estimators = 5000,
min_samples_split=2, min_samples_leaf=1,
max_depth=1, random_state=42
)
gbc_fit.fit(x_train, y_train)
from sklearn.metrics import accuracy_score, classification_report
print( '\nGradient Boost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, gbc_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted'] )
)
print( '\nGradient Boost - Train accuracy',
round( accuracy_score(y_train, gbc_fit.predict(x_train) ),
3
)
)
print( '\ngradient Boost - Train Classification Report\n',
classification_report( y_train, gbc_fit.predict(x_train) )
)
print( '\nGradient Boost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, gbc_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted'] )
)
print( '\nGradient Boost - Test accuracy',
round( accuracy_score(y_test, gbc_fit.predict(x_test) ),
3
)
)
print( '\ngradient Boost - Test Classification Report\n',
classification_report( y_test, gbc_fit.predict(x_test) )
)
If we analyze the results, Gradient boosting has given better results than AdaBoost with the highest possible test accuracy of 87.5% with most 1's captured as 24, compared with AdaBoost with which the test accuracy obtained was 86.8%. Hence, it has been proven that it is no wonder why every data scientist tries to use this algorithm to win competitions!
Extreme gradient boosting - XGBoost classifier
? ? ?XGBoost is the new algorithm developed in 2014 by Tianqi Chen based on the Gradient boosting principles. It has created a storm in the data science community since its inception[?n?sep?n]开始?. XGBoost has been developed with both deep consideration in terms of system optimization and principles in machine learning. The goal of the library is to push the extremes of the computation limits of machines to provide scalable, portable, and accurate results:
# Xgboost Classifier
try:
import xgboost
except ImportError as ex:
print( "Error: the xgboost library is not installed." )
xgboost = None
# Xgboost Classifier
try:
import xgboost as xgb
except ImportError as ex:
print( "Error: the xgboost library is not installed." )
xgboost = None?
xgb_fit = xgb.XGBClassifier( n_estimators=5000,
max_depth=2,
learning_rate=0.05, # eta
random_state = 42, # seed
use_label_encoder=False
)
xgb_fit.fit(x_train, y_train)
print( '\nXGBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, xgb_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Train accuracy',
round( accuracy_score( y_train, xgb_fit.predict(x_train) ),
3
)
)
print( '\nXGBoost - Train Classification Report\n',
classification_report( y_train, xgb_fit.predict(x_train) )
)
print( '\nXGBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, xgb_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Test accuracy',
round( accuracy_score( y_test, xgb_fit.predict(x_test) ),
3
)
)
print( '\nXGBoost - Test Classification Report\n',
classification_report( y_test, xgb_fit.predict(x_test) )
)
The results obtained from XGBoost are almost similar to gradient boosting. The test accuracy obtained was 87.1%, whereas Gradientboost got 87.5%, and also the number of 1's identified is 23 compared with 24 in gradient boosting. The greatest advantage of XGBoost over Gradient boost is in terms of performance and the options available to control model tune. By changing a few of them, makes XGBoost even beat gradient boost as well!
?xgboost参数调节 - 知乎XGBoost Parameters | XGBoost Parameter Tuning
- min_child_weight [default=1]
- Defines the minimum sum of weights of all observations required in a child.
- Used to control over-fitting. Higher values prevent a model from learning relations which might be highly specific to the particular sample selected for a tree.
- 这个参数用来控制过拟合
- Too high values can lead to under-fitting hence, it should be tuned using CV.
- 如果数值太大可能会导致欠拟合
- max_depth [default=6]
- The maximum depth of a tree, same as GBM.
- 控制子树中样本数占总的样本数的最低比例
- 设置树的最大深度
- Used to control over-fitting as higher depth will allow model to learn relations very specific to a particular sample.
- 控制过拟合，如果树的深度太大会导致过拟合
- Should be tuned using CV.
- 应该使用CV来调节。
- Typical values: 3-10
- subsample [default=1]
- Same as the subsample of GBM. Denotes the fraction of observations to be randomly samples for each tree.
- 对原数据集进行随机采样来构建单个树。这个参数代表了在构建树时候 对原数据集采样的百分比。eg：如果设为0.8表示随机抽取样本中80%的个体来构建树。
- Lower values make the algorithm more conservative and prevents overfitting but too small values might lead to under-fitting.
- 相对小点的数值可以防止过拟合，但是过小的数值会导致欠拟合（因为采样过小）。
- Typical values: 0.5-1
- 一般取值 0.5 到 1
- lambda [default=1]
- L2 regularization term on weights (analogous to Ridge regression)
- L2正则项，类似于Ridge Regression
- This used to handle the regularization part of XGBoost. Though many data scientists don’t use it often, it should be explored to reduce overfitting.
- 可以用来考虑降低过拟合，L2本身可以防止过分看重某个特定的特征。尽量考虑尽量多的特征纳入模型。
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
pipeline = Pipeline([
('XGBoost',
xgb.XGBClassifier(
random_state = 42, # random_state
use_label_encoder=False
)
)
])
parameters = {
'XGBoost__n_estimators':(850,5000),# overfit # 2nd step
'XGBoost__max_depth':(2,5), # overfit
'XGBoost__learning_rate':(0.05,), # 1st step
'XGBoost__min_child_weight':(1,6), # 1, 5, 6, 7, 8
'XGBoost__gamma':(0.5,0.6), # acc
'XGBoost__reg_lambda':(1,2), # 0.5, 1, 2
'XGBoost__reg_alpha':(0.1,0.8) # 0, 0.5,0.7, 0.8, 0.9,1.0
}
grid_search = GridSearchCV( pipeline, parameters, n_jobs=-1, cv=5, verbose=3, scoring='accuracy' )
grid_search.fit( x_train, y_train )
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted( parameters.keys() ):
print( '\t%s: %r' % (param_name, best_parameters[param_name] ) )?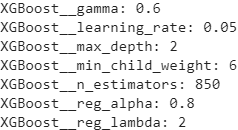
xgb_fit= grid_search
print( '\nXGBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, xgb_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Train accuracy',
round( accuracy_score( y_train, xgb_fit.predict(x_train) ),
3
)
)
print( '\nXGBoost - Train Classification Report\n',
classification_report( y_train, xgb_fit.predict(x_train) )
)
print( '\nXGBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, xgb_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Test accuracy',
round( accuracy_score( y_test, xgb_fit.predict(x_test) ),
3
)
)
print( '\nXGBoost - Test Classification Report\n',
classification_report( y_test, xgb_fit.predict(x_test) )
)
?
VS
xgb_fit = xgb.XGBClassifier( n_estimators=850,
max_depth=2,
learning_rate=0.05, # learning rate
random_state = 42, # random_state
use_label_encoder=False,
min_child_weight=6, #5, 6, 7, 8
gamma=0.5, # acc
#subsample=1,
#colsample_bytree=1,
reg_lambda=1, #,0.5, 1, 2
reg_alpha=0.1, #0, 0.5,0.7, 0.8, 0.9,1.0
)
xgb_fit.fit(x_train, y_train)
print( '\nXGBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, xgb_fit.predict(x_train),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Train accuracy',
round( accuracy_score( y_train, xgb_fit.predict(x_train) ),
3
)
)
print( '\nXGBoost - Train Classification Report\n',
classification_report( y_train, xgb_fit.predict(x_train) )
)
print( '\nXGBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, xgb_fit.predict(x_test),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nXGBoost - Test accuracy',
round( accuracy_score( y_test, xgb_fit.predict(x_test) ),
3
)
)
print( '\nXGBoost - Test Classification Report\n',
classification_report( y_test, xgb_fit.predict(x_test) )
)
? ? ?The results obtained from XGBoost are almost similar to gradient boosting. Just used?850?estimators, the test accuracy obtained was 88.9%, whereas boosting got 87.5%, and also the number of 1's identified is 23 compared with 24 in gradient boosting. The greatest advantage of XGBoost over Gradient boost is in terms of performance and the options available to control model tune. By changing a few of them, I made?XGBoost beat gradient boost as well!
Ensemble of ensembles - model stacking
? ? ?Ensemble of ensembles or model stacking is a method to combine different classifiers into a meta-classifier that has a better generalization performance than each individual classifier in isolation. It is always advisable to take opinions from many people when you are in doubt, when dealing with problems in your personal life too! There are two ways to perform ensembles on models:
- Ensemble with different types of classifiers: In this methodology, different types of classifiers (for example, logistic regression, decision trees, random forest, and so on) are fitted on the same training data and results are combined based on either majority voting or average, based on if it is classification or regression problems.
- Ensemble with a single type of classifiers, but built separately on various bootstrap samples: In this methodology, bootstrap samples are drawn from training data and, each time, separate models will be fitted (individual models could be decision trees, random forest, and so on) on the drawn sample, and all these results are combined at the end to create an ensemble. This method suits dealing with highly flexible models where variance reduction still improves performance.
Ensemble of ensembles with different types of classifiers
? ? ?As briefly mentioned in the preceding section, different classifiers will be applied on the same training data and the results ensembled either taking majority voting cp7_SelectModel_Ensemble Learning_MajorityVoteClassifier_weight_logistic_get_params_bagging_transAxe_Linli522362242的专栏-CSDN博客OR?07_Ensemble Learning and Random Forests_02_AdaBoost_Gradient Boosting_XGBoost_Linli522362242的专栏-CSDN博客or applying another classifier (also known as a meta-classifier) fitted on results obtained from individual classifiers. This means, for meta-classifier X, variables would be model outputs and Y variable would be an actual 0/1 result. By doing this, we will obtain the weightage that should be given for each classifier and those weights will be applied accordingly to classify unseen observations. All three methods of application of ensemble of ensembles are shown here:
- Majority voting or average: In this method, a simple mode function (classification problem) is applied to select the category with the major number of appearances out of individual classifiers. Whereas, for regression problems, an average will be calculated to compare against actual values.cp7_SelectModel_Ensemble Learning_MajorityVoteClassifier_weight_logistic_get_params_bagging_transAxe_Linli522362242的专栏-CSDN博客 OR07_Ensemble Learning and Random Forests_02_AdaBoost_Gradient Boosting_XGBoost_Linli522362242的专栏-CSDN博客
from sklearn.ensemble import VotingClassifier named_estimators =[ ("random_forest_clf", random_forest_clf), ("extra_trees_clf", extra_trees_clf), ("svm_clf", svm_clf), ("mpl_clf", mlp_clf), ] voting_clf = VotingClassifier(named_estimators) voting_clf.fit(X_train,y_train) - Method of application of meta-classifiers on outcomes: Predict actual outcome either 0 or 1 from individual classifiers and apply a meta-classifier on top of 0's and 1's. A small problem with this type of approach is that the meta-classifier will be a bit brittle[?br?tl]易碎的 and rigid[?r?d??d]严格的,死板的. I mean 0's and 1's just gives the result, rather than providing exact sensibility (such as probability).
- Method of application of meta-classifiers on probabilities: In this method, probabilities are obtained from individual classifiers instead of 0's and 1's. Applying meta-classifier on probabilities makes this method a bit more flexible than the first method. Though users can experiment with both methods to see which one performs better. After all, machine learning is all about exploration and trial and error methodologies.
? ? ?In the following diagram, the complete flow of model stacking has been described with various stages:
Steps in the following ensemble with multiple classifiers example:
- Four classifiers have been used separately on training data (logistic regression, decision tree, random forest, and AdaBoost)
- Probabilities have been determined for all four classifiers, however, only the probability for category 1 has been utilized in meta-classifier due to the reason that the probability of class 0?plus?probability of class 1 = 1, hence only one probability is good enough to represent, or else multi-collinearity issues appearing
- Logistic regression has been used as a meta-classifier to model the relationship between four probabilities (obtained from each individual classifier) with respect to a final 0/1 outcome
- Coefficients have been calculated for all four variables used in meta-classifier and applied on new data for calculating the final aggregated probability for classifying observations into the respective categories:
fit_intercept????????bool, default=True
Specifies if a constant (a.k.a. bias or intercept) should be added to the decision function
#Ensemble of Ensembles - by fitting various classifiers
# Hidden:?First consider the high accuracy score,
# and then consider the high recall score
# ==> class weight
clwght = {0:0.3, 1:0.7} # class weight
# Classfier 1 - Logistic Regession
from sklearn.linear_model import LogisticRegression
clf1_logreg_fit = LogisticRegression( fit_intercept = True, class_weight=clwght,
solver = 'liblinear'
)
clf1_logreg_fit.fit( x_train, y_train )
print( '\nLogistic Regression for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf1_logreg_fit.predict( x_train ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nLogistic Regression for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf1_logreg_fit.predict( x_train ) ),
3
)
)
print( '\nLogistic Regression for Ensemble - Train Classification Report\n',
classification_report( y_train, clf1_logreg_fit.predict( x_train ) )
)
######
print( '\nLogistic Regression for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf1_logreg_fit.predict( x_test ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nLogistic Regression for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf1_logreg_fit.predict( x_test ) ),
3
)
)
print( '\nLogistic Regression for Ensemble - Test Classification Report\n',
classification_report( y_test, clf1_logreg_fit.predict( x_test ) )
)
# Classifier 2 – Decision Tree
from sklearn.tree import DecisionTreeClassifier
clf2_dt_fit = DecisionTreeClassifier( criterion='gini', max_depth=5,
min_samples_split=2, min_samples_leaf=2,
random_state=42,
class_weight=clwght
)
clf2_dt_fit.fit( x_train, y_train )
print( '\nDecision Tree for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf2_dt_fit.predict( x_train ),
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\nDecision Tree for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf2_dt_fit.predict(x_train) ),
3
),
)
print( '\nDecision Tree for Ensemble - Train Classification Report\n',
classification_report( y_train, clf2_dt_fit.predict(x_train) )
)
######
print( '\nDecision Tree for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf2_dt_fit.predict( x_test ),
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\nDecision Tree for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf2_dt_fit.predict(x_test) ),
3
),
)
print( '\nDecision Tree for Ensemble - Test Classification Report\n',
classification_report( y_test, clf2_dt_fit.predict(x_test) )
)?
# Classifier 3 – Random Forest
from sklearn.ensemble import RandomForestClassifier
clf3_rf_fit = RandomForestClassifier( n_estimators=10000, # 5000
criterion='gini',
max_depth=6, # 2, 5
min_samples_split=2,
min_samples_leaf=1, class_weight=clwght
)
clf3_rf_fit.fit( x_train, y_train )
print( '\nRandom Forest for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf3_rf_fit.predict( x_train ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nRandom Forest for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf3_rf_fit.predict(x_train) ),
3
)
)
print( '\nRandom Forest for Ensemble - Train Classification Report\n',
classification_report( y_train, clf3_rf_fit.predict(x_train) ),
)
######
print( '\nRandom Forest for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf3_rf_fit.predict( x_test ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nRandom Forest for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf3_rf_fit.predict(x_test) ),
3
)
)
print( '\nRandom Forest for Ensemble - Test Classification Report\n',
classification_report( y_test, clf3_rf_fit.predict(x_test) ),
)?
#################Change some parameter values
# Classifier 3 – Random Forest
from sklearn.ensemble import RandomForestClassifier
clwght = {0:0.3, 1:0.7} # class weight
clf3_rf_fit = RandomForestClassifier( n_estimators=2500, #### 10000
criterion='gini',
max_depth=5, #### 5,6
min_samples_split=2,
min_samples_leaf=1, class_weight=clwght
)
clf3_rf_fit.fit( x_train, y_train )
print( '\nRandom Forest for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf3_rf_fit.predict( x_train ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nRandom Forest for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf3_rf_fit.predict(x_train) ),
3
)
)
print( '\nRandom Forest for Ensemble - Train Classification Report\n',
classification_report( y_train, clf3_rf_fit.predict(x_train) ),
)
######
print( '\nRandom Forest for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf3_rf_fit.predict( x_test ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nRandom Forest for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf3_rf_fit.predict(x_test) ),
3
)
)
print( '\nRandom Forest for Ensemble - Test Classification Report\n',
classification_report( y_test, clf3_rf_fit.predict(x_test) ),
)
Better!
#################
# Classifier 4 - Adaboost classifier
from sklearn.ensemble import AdaBoostClassifier
clf4_dtree = DecisionTreeClassifier( criterion='gini', max_depth=1,
class_weight = clwght
)
clf4_adabst_fit = AdaBoostClassifier( base_estimator=clf4_dtree,
n_estimators=5000, learning_rate=0.05,
random_state=42
)
clf4_adabst_fit.fit( x_train, y_train )
print( '\nAdaBoost for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf4_adabst_fit.predict( x_train ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nAdaBoost for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf4_adabst_fit.predict( x_train ) ),
3
)
)
print( '\nAdaBoost for Ensemble - Train Confusion Report\n',
classification_report( y_train, clf4_adabst_fit.predict( x_train ) ),
)
######
print( '\nAdaBoost for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf4_adabst_fit.predict( x_test ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nAdaBoost for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf4_adabst_fit.predict( x_test ) ),
3
)
)
print( '\nAdaBoost for Ensemble - Test Confusion Report\n',
classification_report( y_test, clf4_adabst_fit.predict( x_test ) ),
)?
#################Change some parameter values
# Classifier 4 - Adaboost classifier
from sklearn.ensemble import AdaBoostClassifier
clf4_dtree = DecisionTreeClassifier( criterion='gini', max_depth=1,
class_weight = clwght
)
clf4_adabst_fit = AdaBoostClassifier( base_estimator=clf4_dtree,
n_estimators=2500, #5000
learning_rate=0.05,
random_state=42,
algorithm='SAMME.R'
)
clf4_adabst_fit.fit( x_train, y_train )
print( '\nAdaBoost for Ensemble - Train Confusion Matrix\n\n',
pd.crosstab( y_train, clf4_adabst_fit.predict( x_train ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nAdaBoost for Ensemble - Train accuracy',
round( accuracy_score( y_train, clf4_adabst_fit.predict( x_train ) ),
3
)
)
print( '\nAdaBoost for Ensemble - Train Confusion Report\n',
classification_report( y_train, clf4_adabst_fit.predict( x_train ) ),
)
######
print( '\nAdaBoost for Ensemble - Test Confusion Matrix\n\n',
pd.crosstab( y_test, clf4_adabst_fit.predict( x_test ),
rownames = ['Actuall'], colnames = ['Predicted']
)
)
print( '\nAdaBoost for Ensemble - Test accuracy',
round( accuracy_score( y_test, clf4_adabst_fit.predict( x_test ) ),
3
)
)
print( '\nAdaBoost for Ensemble - Test Confusion Report\n',
classification_report( y_test, clf4_adabst_fit.predict( x_test ) ),
)?
Better!
850 n_estimators, Great!But it will reduce the performance of ensemble's meta-classifier, so I use 2500
?this result from the following code
?#################
?In the following step, we perform an ensemble of classifiers:
ensemble = pd.DataFrame()on the same training data?the results ensembled and?then?applying another classifier (also known as a meta-classifier) fitted on results obtained from individual classifiers?
? ? ?In the following step, we take probabilities only for category 1, as it gives intuitive sense for high probability and indicates the value towards higher class 1. But this should not stop someone if they really want to fit probabilities on a 0 class instead. In that case, low probability values are preferred for category 1, which gives us a little bit of a headache!
# LogisticRegression Classifier # [1]: get the class '1' probabilities
ensemble['log_output_one'] = pd.DataFrame( clf1_logreg_fit.predict_proba( x_train ) )[1]
# Decision Tree Classifier
ensemble['dtr_output_one'] = pd.DataFrame( clf2_dt_fit.predict_proba( x_train ) )[1]
# RandomForestClassifier
ensemble['rf_output_one'] = pd.DataFrame( clf3_rf_fit.predict_proba( x_train ) )[1]
# Adaboost classifier
ensemble['adb_output_one'] = pd.DataFrame( clf4_adabst_fit.predict_proba( x_train ) )[1]
ensemble = pd.concat( [ ensemble,
pd.DataFrame(y_train).reset_index( drop=True ),
], # y_train is a pandas series
axis=1
)
# Fitting meta-classifier
meta_logit_fit = LogisticRegression( fit_intercept=False )
meta_logit_fit.fit( ensemble[ ['log_output_one', 'dtr_output_one',
'rf_output_one', 'adb_output_one'
]
],
ensemble['Attrition_ind'], # y_actual
)
?
?
==>
==>
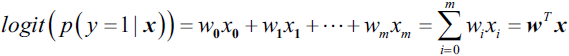
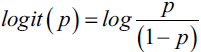
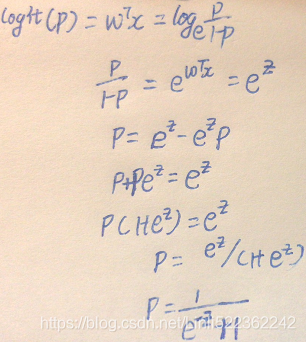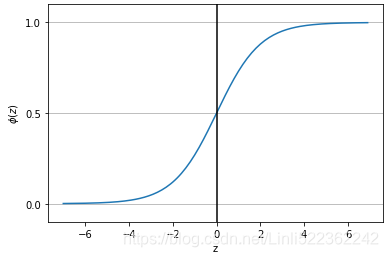
? ? ?Here z is the net input, the linear combination of weights and sample features(here is weak learner's output probabilities),?
?==>
coefs = meta_logit_fit.coef_
coefs?
ensemble
ensemble_test = pd.DataFrame()
# LogisticRegression Classifier # [1]: get the class '1' probabilities
ensemble_test['log_output_one'] = pd.DataFrame( clf1_logreg_fit.predict_proba( x_test ) )[1]
# Decision Tree Classifier
ensemble_test['dtr_output_one'] = pd.DataFrame( clf2_dt_fit.predict_proba( x_test ) )[1]
# RandomForestClassifier
ensemble_test['rf_output_one'] = pd.DataFrame( clf3_rf_fit.predict_proba( x_test ) )[1]
# Adaboost classifier
ensemble_test['adb_output_one'] = pd.DataFrame( clf4_adabst_fit.predict_proba( x_test ) )[1]
ensemble_test = pd.concat( [ ensemble_test,
pd.DataFrame(y_test).reset_index( drop=True ),
], # note: y_test is a pandas series
axis=1
)
ensemble_test['all_one']=meta_logit_fit.predict( ensemble_test[ ['log_output_one',
'dtr_output_one',
'rf_output_one',
'adb_output_one'
]
]
)
ensemble_testensemble_test['all_one'] is the prediction of?meta-classifier
print( '\n\nEnsemble of Models - Test Confusion Matrix\n\n',
pd.crosstab( ensemble_test['Attrition_ind'], ensemble_test['all_one'],
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\n\nEnsemble of Models - Test Accuracy',
round( accuracy_score( ensemble_test['Attrition_ind'], ensemble_test['all_one'] ),
3
)
)
print( '\nEnsemble of Models - Test Classification Report\n',
classification_report( ensemble_test['Attrition_ind'], ensemble_test['all_one'] )
)
? ? ?Though code prints Train, Test accuracies, Confusion Matrix, and Classification Reports, we have not shown them here due to space constraints. Users are advised to run and check the results on their computers. Test accuracy came as 87.3%, which is near the highest value of the gradient boosting results(87.5%). However, by careful tuning, ensembles do give much better results based on adding better models and removing models with low weights:
print( 'Co-efficients for LR, DT, RF and AB are:', coefs )
? ? ?It seems that, surprisingly, AdaBoost is dragging down performance of the ensemble. A tip is to either change the parameters used in AdaBoost and rerun the entire exercise, or remove the AdaBoost classifier from the ensemble and rerun the ensemble step to see if there is any improvement in ensemble test accuracy, precision, and recall values:
I disagree with this suggestion
# let's remove the decision tree classifier since AdaBoost and RandomForest both built based on tree. Besides, I also change some parameter values of? the previous weak learners:
ensemble = pd.DataFrame()
# LogisticRegression Classifier # [1]: get the class '1' probabilities
ensemble['log_output_one'] = pd.DataFrame( clf1_logreg_fit.predict_proba( x_train ) )[1]
# Decision Tree Classifier
# ensemble['dtr_output_one'] = pd.DataFrame( clf2_dt_fit.predict_proba( x_train ) )[1]
# RandomForestClassifier
ensemble['rf_output_one'] = pd.DataFrame( clf3_rf_fit.predict_proba( x_train ) )[1]
# Adaboost classifier
ensemble['adb_output_one'] = pd.DataFrame( clf4_adabst_fit.predict_proba( x_train ) )[1]
ensemble = pd.concat( [ ensemble,
pd.DataFrame(y_train).reset_index( drop=True ),
],
axis=1
)
# Fitting meta-classifier
meta_logit_fit = LogisticRegression( fit_intercept=False )
meta_logit_fit.fit( ensemble[ ['log_output_one',
# 'dtr_output_one',
'rf_output_one',
'adb_output_one'
]
],
ensemble['Attrition_ind'], # y_actual
)ensemble_test = pd.DataFrame()
# LogisticRegression Classifier # [1]: get the class '1' probabilities
ensemble_test['log_output_one'] = pd.DataFrame( clf1_logreg_fit.predict_proba( x_test ) )[1]
# Decision Tree Classifier
#ensemble_test['dtr_output_one'] = pd.DataFrame( clf2_dt_fit.predict_proba( x_test ) )[1]
# RandomForestClassifier
ensemble_test['rf_output_one'] = pd.DataFrame( clf3_rf_fit.predict_proba( x_test ) )[1]
# Adaboost classifier
ensemble_test['adb_output_one'] = pd.DataFrame( clf4_adabst_fit.predict_proba( x_test ) )[1]
ensemble_test = pd.concat( [ ensemble_test,
pd.DataFrame(y_test).reset_index( drop=True ),
], # note: y_test is a pandas series
axis=1
)
ensemble_test['all_one']=meta_logit_fit.predict( ensemble_test[ ['log_output_one',
# 'dtr_output_one',
'rf_output_one',
'adb_output_one'
]
]
)print( '\n\nEnsemble of Models - Test Confusion Matrix\n\n',
pd.crosstab( ensemble_test['Attrition_ind'], ensemble_test['all_one'],
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\n\nEnsemble of Models - Test Accuracy',
round( accuracy_score( ensemble_test['Attrition_ind'], ensemble_test['all_one'] ),
3
)
)
print( '\nEnsemble of Models - Test Classification Report\n',
classification_report( ensemble_test['Attrition_ind'], ensemble_test['all_one'] )
)# 88.7% > 87.5%?
?#?I get a better accuracy and recall score
print( 'Co-efficients for LR, RF and AB are:', coefs )?
Summary:?
Removal of a weak learner can increase the coefficient value of other weak learners, improve the accuracy of the other weak learners(or weak classifiers) （Strong alliance）, and also affect the coefficient value of the weak learner, which in turn affects the accurate score of ensemble (here also includes the recall rate of class 1)
Ensemble of ensembles with bootstrap samples using a single type of classifier
? ? ?In this methodology, bootstrap samples are drawn randomly with replacement from training data and, each time, separate models will be fitted (individual models could be decision trees, random forest, and so on) on the drawn sample, and all these results are combined at the end to create an ensemble. This method suits dealing with highly flexible models where variance reduction will still improve performance:
? ? ?In the following example, AdaBoost is used as a base classifier and the results of individual AdaBoost models are combined using the bagging classifier to generate final outcomes. Nonetheless, each AdaBoost is made up of decision trees with a depth of 1 (decision stumps). Here, we would like to show that classifier inside classifier inside classifier is possible (sounds like the Inception movie盗梦空间 though!):
# Ensemble of Ensembles - by applying bagging on simple classifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import AdaBoostClassifier
clwght = {0:0.3, 1:0.7}?The following is the base classifier (decision stump) used in the AdaBoost classifier:
eoe_dtree = DecisionTreeClassifier( criterion='gini',
max_depth=1,
class_weight = clwght
)Each AdaBoost classifier consists of 850 decision trees with a learning rate of 0.05:
eoe_adabst_fit = AdaBoostClassifier( base_estimator = eoe_dtree,
n_estimators=850,
learning_rate=0.05,
random_state=42
)
eoe_adabst_fit.fit( x_train, y_train )
print( '\nAdaBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, eoe_adabst_fit.predict( x_train ),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nAdaBoost - Train accuracy',
round( accuracy_score( y_train, eoe_adabst_fit.predict(x_train) ),
3
)
)
print( '\nAdaBoost - Train Classification Report\n',
classification_report( y_train, eoe_adabst_fit.predict(x_train) )
)
######
print( '\nAdaBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, eoe_adabst_fit.predict( x_test ),
rownames=['Actuall'], colnames=['Predicted']
)
)
print( '\nAdaBoost - Test accuracy',
round( accuracy_score( y_test, eoe_adabst_fit.predict(x_test) ),
3
)
)
print( '\nAdaBoost - Test Classification Report\n',
classification_report( y_test, eoe_adabst_fit.predict(x_test) )
)n_estimators=850 in?AdaBoost(better)? ? ? ? ?n_estimators=500 in?AdaBoost
?VS?
?The bagging classifier consists of 50 AdaBoost classifiers to ensemble the ensembles:
# ?In a bagging procedure, rows are sampled while selecting all the column variables
bag_fit = BaggingClassifier( base_estimator = eoe_adabst_fit,
n_estimators=50,
max_samples=1.0,
max_features=1.0,
bootstrap=True, # with replacement
bootstrap_features=False, # without replacement
n_jobs = -1,
random_state=42
)
bag_fit.fit(x_train, y_train)
print( '\nEnsemble of AdaBoost - Train Confusion Matrix\n\n',
pd.crosstab( y_train, bag_fit.predict(x_train),
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\nEnsemble of AdaBoost - Train accuracy',
round( accuracy_score( y_train, bag_fit.predict(x_train) ),
3
)
)
print( '\nEnsemble of AdaBoost - Train Classification Report\n',
classification_report( y_train, bag_fit.predict(x_train) )
)
######
print( '\nEnsemble of AdaBoost - Test Confusion Matrix\n\n',
pd.crosstab( y_test, bag_fit.predict(x_test),
rownames = ['Actuall'], colnames=['Predicted']
)
)
print( '\nEnsemble of AdaBoost - Test accuracy',
round( accuracy_score( y_test, bag_fit.predict(x_test) ),
3
)
)
print( '\nEnsemble of AdaBoost - Train Classification Report\n',
classification_report( y_test, bag_fit.predict(x_test) )
)n_estimators=850 in?AdaBoost? ? ? ? ? ? ? ? ? ? ?n_estimators=500 in?AdaBoost(better)
vs
the parameter adjustment of the weak learners should consider the overall performance of the ensemble classifer
? ? ?The results of the ensemble on AdaBoost have shown some improvements, in which the test accuracy obtained is 87.1%, which is almost to that of gradient boosting at 87.5%. However, the number of 1's identified is 25 here, which is greater than Gradient Boosting. Hence, it has been proven that an ensemble of ensembles does work! ?
Summary
? ? ?In this chapter, you have learned the complete details about tree-based models, which are currently the most used in the industry, including individual decision trees with grid search and an ensemble of trees such as bagging, random forest, boosting (including AdaBoost, gradient boost and XGBoost), and finally, ensemble of ensembles, also known as model stacking, for further improving accuracy by reducing variance errors by aggregating results further. In model stacking, you have learned how to determine the weights for each model, so that decisions can be made as to which model to keep in the final results to obtain the best possible accuracy.
? ? ?In the next chapter, you will be learning k-nearest neighbors and Naive Bayes, which are
less computationally intensive than tree-based models. The Naive Bayes model will be explained with an NLP use case. In fact, Naive Bayes and SVM are often used where variables (number of dimensions) are very high in number to classify.