[游戏开发]【图形学基础】Unity直观感受矩阵是如何影响点的

刚手推完矩阵，正好就学到一篇用正方体模拟顶点和矩阵做运算的文章

文章链接

这个DEMO是把每一个正方体预制件当成一个顶点，然后通过顶点直接和这些顶点的位置做运算，让我们可以更直观的看到矩阵是如何影响每一个顶点，进而影响一整个物体的

首先是整个操控脚本，这里有一个小技巧，通过GetCompents可以获得组件上所有的具有相同父类的脚本。然后所有的变换矩阵都继承自同一个变换父类Transformation，于是就可以通过这个方法得到所有的变换矩阵

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class TransformationGrid : MonoBehaviour
{
    public Transform prefab;
    public int gridResolution = 10;

    //学会了，还可以声明Transform数组，那么之前A*算法的代码应该会更简洁
    Transform[] grid;
    Matrix4x4 transformation;

    List<Transformation> transformations;//存储连续的变换矩阵

    Vector3 GetCoordinates(int x,int y,int z)
    {
        return new Vector3
        (
            x - (gridResolution -1) *0.5f,
            y - (gridResolution -1) *0.5f,
            z - (gridResolution -1) *0.5f
        );
    }

    Transform CreateGridPoint(int x,int y,int z)//创建预制体
    {
        Transform point = Instantiate<Transform>(prefab);
        point.localPosition = GetCoordinates(x, y, z);
        point.GetComponent<MeshRenderer>().material.color = new Color(//对颜色做一个插值
            (float)x/gridResolution,
            (float)y/gridResolution,
            (float)z/gridResolution
            );
        return point;
    }

    private void Awake()
    {
        transformations = new List<Transformation>();//初始化一下列表
        grid = new Transform[gridResolution * gridResolution * gridResolution];//立方体数组
        for(int i = 0, z = 0; z < gridResolution; z++)
        {
            for(int y = 0; y < gridResolution; y++)
            {
                for(int x = 0;x<gridResolution;x++,i++)
                {
                    grid[i] = CreateGridPoint(x, y, z);
                }
            }
        }
    }

    private void Update()
    {
        UpdateTransformation();
        GetComponents<Transformation>(transformations);//将得到的参数放入transformations中
        for (int i = 0, z = 0; z < gridResolution; z++)
        {
            for (int y = 0; y < gridResolution; y++)
            {
                for (int x = 0; x < gridResolution; x++, i++)
                {
                    grid[i].localPosition = TransformPoint(x, y, z);
                }
            }
        }
    }

    void UpdateTransformation()//将所有的矩阵全部综合算成一个矩阵，这样可以节省性能
    {
        GetComponents<Transformation>(transformations);//将得到的参数放入transformations中
        if (transformations.Count > 0)
        {
            transformation = transformations[0].Matrix;
            for(int i=1;i<transformations.Count;i++)
            {
                transformation = transformations[i].Matrix * transformation;
            }
        }
    }

    Vector3 TransformPoint(int x,int y,int z)
    {
        Vector3 coordinates = GetCoordinates(x, y, z);
        return transformation.MultiplyPoint(coordinates);//这个函数的意思是矩阵乘上点
    }

}

//记录一个操作
//使用GetCompents去获取 组件上 所有继承自同一个父类的脚本组件，然后统一调用虚函数完成点和矩阵的变换
//又学到了

所有变换矩阵的公共父类Transformation

public abstract class Transformation : MonoBehaviour
{
    public abstract Vector3 Apply(Vector3 point);//统一的矩阵以用接口
    public abstract Matrix4x4 Matrix { get; }
}

缩放矩阵：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class ScaleTransformation : Transformation
{
    public Vector3 scale;
    public override Vector3 Apply(Vector3 point)
    {
        point.x *= scale.x;
        point.y *= scale.y;
        point.z *= scale.z;
        return point;
    }
    public override Matrix4x4 Matrix
    {
        get
        {
            Matrix4x4 matrix = new Matrix4x4();//设置缩放矩阵
            matrix.SetRow(0, new Vector4(scale.x, 0f, 0f, 0f));
            matrix.SetRow(1, new Vector4(0f, scale.y, 0f, 0f));
            matrix.SetRow(2, new Vector4(0f, 0f, scale.z, 0f));
            matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
            return matrix;
        }
    }
}

旋转矩阵：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class RotationTransformation : Transformation
{
    public Vector3 rotation;

    public override Vector3 Apply(Vector3 point)
    {
        float radX = rotation.x * Mathf.Deg2Rad;
        float radY = rotation.y * Mathf.Deg2Rad;
        float radZ = rotation.z * Mathf.Deg2Rad;//将度转换为弧度制然后去计算旋转后的坐标
        float sinX = Mathf.Sin(radX);
        float cosX = Mathf.Cos(radX);
        float sinY = Mathf.Sin(radY);
        float cosY = Mathf.Cos(radY);
        float sinZ = Mathf.Sin(radZ);
        float cosZ = Mathf.Cos(radZ);

        Vector3 xAxis = new Vector3(
                cosY*cosZ,
                cosX*sinZ + sinX*sinY*cosZ,
                sinX*sinZ - cosX*sinY*cosZ
            );
        Vector3 yAxis = new Vector3(
                -cosY*sinZ,
                cosX*cosZ - sinX*sinY*sinZ,
                sinX*cosZ + cosX*sinY*sinZ
            );
        Vector3 zAxis = new Vector3(
                sinY,
                -sinX*cosY,
                cosX*cosY
            );

        return xAxis * point.x + yAxis * point.y + zAxis * point.z;
    }

    public override Matrix4x4 Matrix
    {
        get
        {
            float radX = rotation.x * Mathf.Deg2Rad;
            float radY = rotation.y * Mathf.Deg2Rad;
            float radZ = rotation.z * Mathf.Deg2Rad;//将度转换为弧度制然后去计算旋转后的坐标
            float sinX = Mathf.Sin(radX);
            float cosX = Mathf.Cos(radX);
            float sinY = Mathf.Sin(radY);
            float cosY = Mathf.Cos(radY);
            float sinZ = Mathf.Sin(radZ);
            float cosZ = Mathf.Cos(radZ);

            Matrix4x4 matrix = new Matrix4x4();
            matrix.SetColumn(0, new Vector4(
                cosY * cosZ,
                cosX * sinZ + sinX * sinY * cosZ,
                sinX * sinZ - cosX * sinY * cosZ,
                0f
            ));
            matrix.SetColumn(1, new Vector4(
                -cosY * sinZ,
                cosX * cosZ - sinX * sinY * sinZ,
                sinX * cosZ + cosX * sinY * sinZ,
                0f
            ));
            matrix.SetColumn(2, new Vector4(
                sinY,
                -sinX * cosY,
                cosX * cosY,
                0f
            ));
            matrix.SetColumn(3, new Vector4(0f,0f,0f,1f));
            return matrix;
        }
    }
}

位移矩阵：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PositionTransformation : Transformation
{
    public Vector3 position;
    public override Vector3 Apply(Vector3 point)
    {
        return point + position;
    }

    public override Matrix4x4 Matrix
    {
        get
        {
            //设置位移矩阵
            Matrix4x4 matrix = new Matrix4x4();
            matrix.SetRow(0, new Vector4(1f, 0f, 0f, position.x));
            matrix.SetRow(1, new Vector4(0f, 1f, 0f, position.y));
            matrix.SetRow(2, new Vector4(0f, 0f, 1f, position.z));
            matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
            return matrix;
        }
    }
}

模仿投影矩阵

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class CameraTransform : Transformation
{
    public float focalLength = 0f;
    // Start is called before the first frame update
    public override Vector3 Apply(Vector3 point)
    {
        return point;//暂时不用这个方法了
    }

    public override Matrix4x4 Matrix
    {
        get
        {
            Matrix4x4 matrix = new Matrix4x4();
            matrix.SetRow(0, new Vector4(focalLength, 0f, 0f, 0f));
            matrix.SetRow(1, new Vector4(0f, focalLength, 0f, 0f));
            matrix.SetRow(2, new Vector4(0f, 0f, 0f, 0f));
            matrix.SetRow(3, new Vector4(0f, 0f, 1f, 0f));
            return matrix;
        }
    }
}

使用方法就是将这些脚本依次挂在摄像机上即可

效果大致如下图

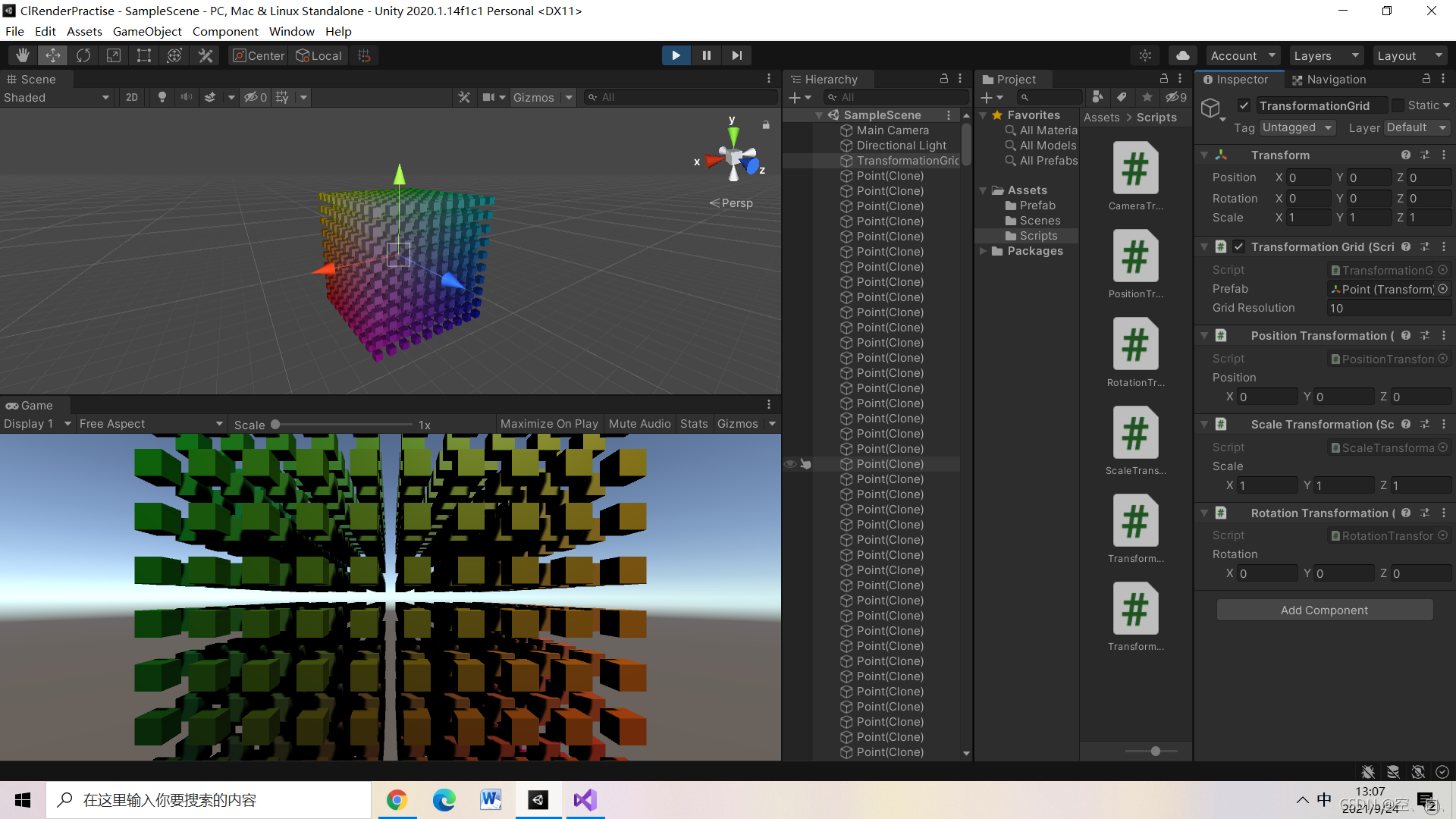
矩阵是如何推出来的可以参考链接文章