unity3d版本-version2017
参考文献:
(1)部分内容由千峰教育(莫新宇)听课笔记总结
Transform组件特点
1)控制游戏对象的变换、包含父子关系的内容
2)关于坐标 世界坐标(以场景的原点为原点);本地坐标(相对于父物体的坐标) 以父物体的位置为原点
3)关于旋转 世界旋转/本地旋转(相对于父物体的旋转)
(1)坐标系内容
?在Unity3D中,分为世界坐标系、屏幕坐标系、视口坐标系
了解左手坐标系的概念
没有父物体时,localPosition与position等价
localPosition 和 position 的区别就在于:前者是相对父物体的相对世界坐标;后者是在初始化空间里的绝对世界坐标;当然,如果一个物体没有父物体,则二者等效。
其中,在Unity3D的Inspector面板中,显示的便是每一个物体的localPosition 数值。
InverseTransformVector 和 TransformPoint上述二者,实现localPosition 和postion 的互相转化
#1 : 求A物体下相对坐标为(10, 10, 10)的物体,其绝对世界坐标是多少??
A.tranform.TransformPoint(new Vector3(10, 10, 10));
#2 : 求绝对世界坐标为(20, -20, 20)的物体,相对于A物体的相对世界坐标是多少?
A.tranform.InverseTransformVector(new Vector3(20, -20, 20));


子物体显示的是相对于父物体的变换
子物体世界坐标=子物体本地坐标+父物体的世界坐标
子物体世界旋转=子物体本地旋转+父物体的世界旋转
子物体世界缩放=子物体本地缩放+父物体的世界缩放
基础知识总结
normalized 当前向量的标准化向量(归一化)
Normalize()
magnitude 向量的模,长度
sqrMagnitude 模的平方 比较两个向量的长度
static forword 世界的前方 (0,0,1)
static right 世界的右方(1,0,0)
static up 世界的上方(0,1,0)
static zero 0,0,0
static one1,1,1
static float Distance(Vector3,Vector3)求两个点的距离
static float Angle(Vector3,Vector3)求两个向量的夹角
static Vector3 Cross(Vector3a,Vector3b)求两个向量的叉乘
(2)旋转的概念
?欧拉角EularAngle
物体绕x,y,z轴(世界的)旋转角度
优点:好理解,好操作
角色方向控制:transform.eulerAngles += Vector3.up * hor * turnSpeed;
缺点:容易出现多个欧拉角的值表示一个旋转
四元数
由四个值组成x,y,z,w;优点:可以避免欧拉角及万向锁存在的问题
Rotation是一个四元数,而其数值的正负值往往代表的是旋转方向,而其数值大小0到1则对应0到180度的对应Rotation
Rotate:
- 旋转通常以欧拉角而不是四元数
- Rotate将Vector3参数作为欧拉角。第二个参数是旋转轴,可以将其设置为局部轴(Space.Self)或全局轴(Space.World)。旋转是欧拉量
具体使用方法的几种案例:
?1)相对于世界坐标
void Update () {
? ? ? ? transform.Rotate(Vector3.left, Space.World); //左手坐标系,绕x轴旋转
? ? ? ? Debug.Log(transform.eulerAngles);
?? ?}?
 2)相对于局部坐标,也就是自身坐标
2)相对于局部坐标,也就是自身坐标
?transform.Rotate(Vector3.forward, Space.Self);
3)基本用法
? ? ? ? float speed = 3f;
?? ?void Update () {
? ? ? ? Vector3 v3 = new Vector3(10, 10, 10);
? ? ? ? transform.Rotate(v3*turnSpeed*Time.deltaTime);
? ? ? ? Debug.Log(transform.eulerAngles);
? ? }
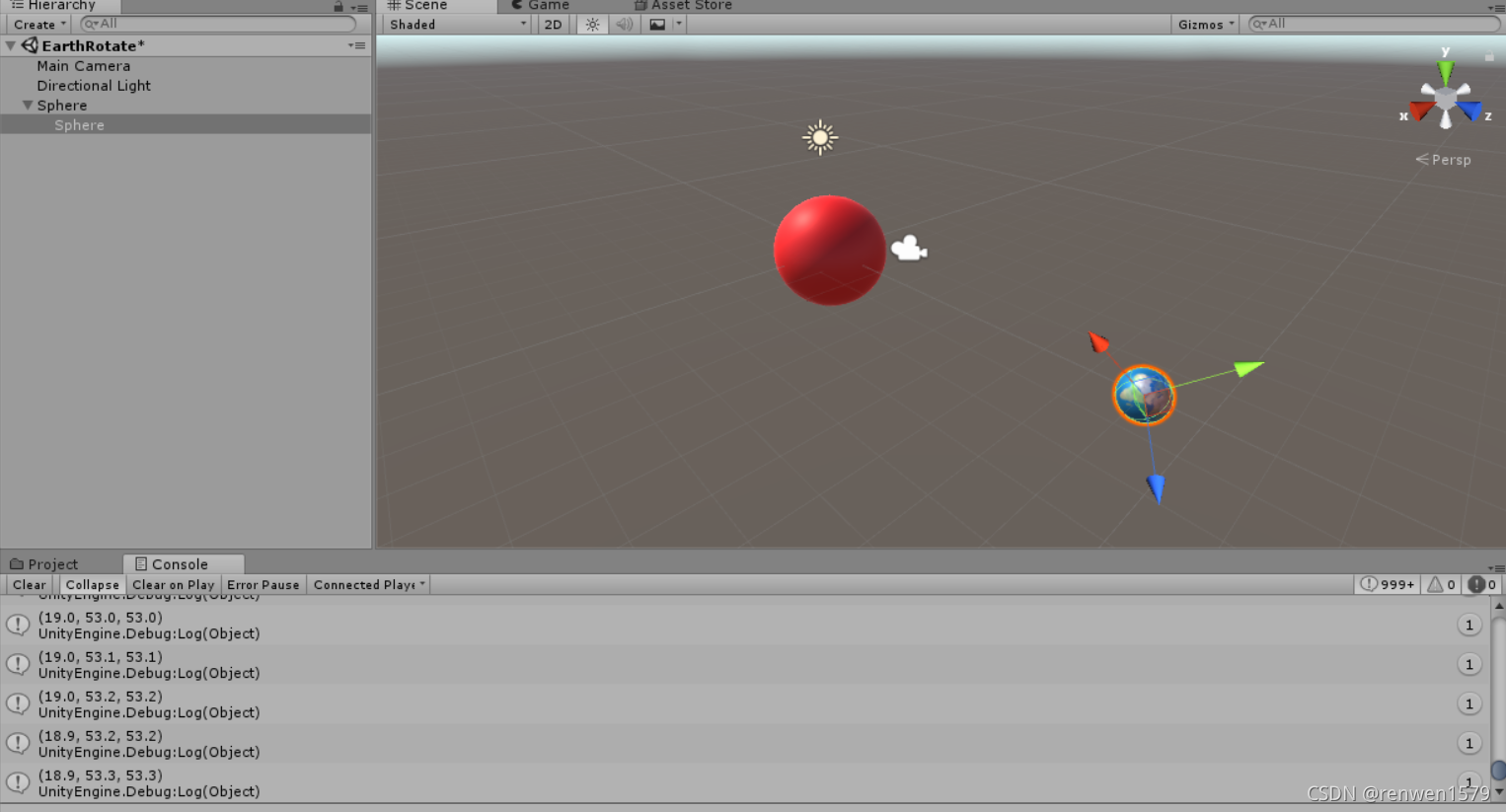
绕着Vector3(10,10,10)这个轴进行转动
eulerAngles:
Transform.eulerAngles表示世界空间中的旋转。在检查器中查看GameObject的旋转时,可能会看到与此属性中存储的角度值不同的角度值。这是因为Inspector显示本地旋转,可以使用Transform.localEulerAngles来查看本地的角度显示。
键盘控制物体转动的代码为:
?控制物体方向的常见代码为:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class earthMove : MonoBehaviour {
? ? public float turnSpeed = 0.3f;
? ? private float hor;
?? ?// Use this for initialization
?? ?void Start () {
? ? ? ??
?? ?}
?? ?
?? ?// Update is called once per frame
?? ?void Update () {
? ? ? ? hor=Input.GetAxis("Horizontal"); //获取方向键
? ? ? ? transform.eulerAngles += Vector3.up * hor * turnSpeed;
? ? ? ? Debug.Log(transform.eulerAngles);
?? ?}
}


欧拉角与四元数的转换
//将欧拉角转换为四元数
?Quaternion qua=Quaternion.Euler(new Vector3(x,y,z));
Quaternion结构体的3个方法:?
Static identity 空旋转
Static LookRotation 将一个向量转换为这个方向所代表的四元数
Static Lerp 插值,有过渡动画
关于Transform.eulerAngles
最需要注意的一点是欧拉角的读取数值是介于0到360度的,所以无论读写,可能数值与Transform面板数值不同,同时,最重要的一点,由于这种特性,对其数值的累加可能出错
Quaternion:
Unity提供了将欧拉角转换为四元数的方法,可以使用Quaternion.Lerp()方法来完成,这是一种插值旋转方法,所以旋转速度会越来越慢,适合模拟减速效果:
transform.rotation = Quaternion.Lerp(transform.rotation, Quaternion.Euler(0, 0, 90), 0.05f);
Quaternion方法:
Quaternion.RotateTowards():插值旋转至与目标角度相同
Quaternion.LookRotation():插值旋转看向目标
可以通过上面两种方法完成看向目标,或与目标角度一致,具体用法可以为:
? ? ? ? //与target保持一样的角度
? ? ? ? transform.rotation = Quaternion.RotateTowards(transform.rotation,target.rotation,2f);
? ? ? ? //看向目标
? ? ? ? transform.rotation = Quaternion.LookRotation(target.position);
Transform.RotateAround 围绕旋转
gameObject.transform.RotateAround(new Vector3(x,y,z),new Vector3(x,y,z),Speed)
其中,第一个vector3表示围绕中心点坐标,第二个vector3表示所围绕旋转的轴,Speed表示旋转速度。
范例用途:比如太阳系行星旋转
了解向量的内容后,为主摄像机添加脚本
范例:
照相机跟随
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CameraMove : MonoBehaviour {
? ? [Header("跟随目标")]
? ? public Transform fllowTarget;
? ? private Vector3 dir;
?? ?// Use this for initialization
?? ?void Start () {
? ? ? ? dir = fllowTarget.position - transform.position;
?? ?}
//awake()一般用来寻找对象,如Tag
? ? private void Awake()
? ? {
? ? ? ??
? ? }
? ? // Update is called once per frame
? ? void Update () {
? ? ? ? transform.position = fllowTarget.position - dir;
?? ?}
}
?
?