开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 游戏开发 -> unity3D数学基础-坐标系、向量、矩阵 -> 正文阅读

[游戏开发]unity3D数学基础-坐标系、向量、矩阵

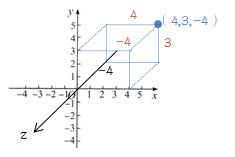
坐标系

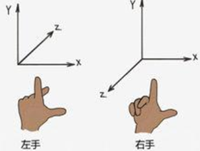
左右手坐标系

左手坐标系：伸开左手，大拇指指向X轴正方向，食指指向Y轴正方向，其他三个手指指向Z轴正方向。
右手坐标系：伸开右手，大拇指指向X轴正方向，食指指向Y轴正方向，其他三个手指指向Z轴正方向。

3D笛卡尔坐标系：右手坐标系
OpenGL：右手坐标系
Direct3D：左手坐标系
Unity3D：左手坐标系（世界坐标系），即+x, +y, +z分别指向右方，上方和前方。????

各种坐标空间(坐标系)

部分空间种类

模型空间

unity约定：使用的左手坐标系，XYZ分别对应着右上前。
模型空间的原点和坐标轴通常由美术人员在建模软件里确定好的。当导入到unity中，我们可以在顶点着色器中访问到模型的顶点信息，其中包含了每个顶点的坐标，这些坐标都是相对于模型空间中的原点（通常位于模型的重心）定义的。
检视视图中显示的为localPosition的值。
transform.localPosition（本地坐标）可以获得物体在父物体的局部坐标系中的位置点。

世界空间

unity约定：使用左手坐标系，但它的XYZ轴是固定不变的。
transform.position来获取游戏对象的世界坐标。

观察空间

右手坐标系，这是符合OpenGL传统的，再这样的观察空间中，摄像机的正前方向指的是-z轴方向。
unity约定：摄像机位于原点，+x轴指向右方，+y轴指向上分，而+z轴指向的是摄像机的后方。

裁切空间

目标是能够方便地对渲染图元进行裁剪：完全位于这块空间内部的图元将会被保留，完全位于这块空间外部的图元将会被剔除，而与这块空间边界相交的图元就会被裁剪。
这块空间是由视椎体来决定。

屏幕空间

左手坐标系
以像素来定义的，屏幕的左下角为（0,0），右上角为（Screen.width, Screen.height），z轴的坐标是相机的世界坐标中z轴坐标的负值。
屏幕空间是一个二维空间。
鼠标位置坐标属于屏幕坐标，通过Input.mousePosition可以获得该位置的坐标。
手指触摸屏幕也为屏幕坐标，Input.GetTouch(0).position可以获得单个手指触摸屏幕时手指的坐标。

视口空间

将Game视图的屏幕坐标系单位化
左下角（0,0），右上角（1,1）。z轴的坐标是相机的世界坐标中z轴坐标的负值。

相互空间转换

shader中空间转换

模型变换：顶点变换的第一步就是将顶点从模型空间变换到世界空间中。这个变换通常叫做模型变换。注意这里的变换顺序是不能互换的，即先进行缩放，然后进行旋转，最后是平移，然后我们可以构建出模型变换的变换矩阵(因为矩阵不满足交换律，所以不要随便调换变换顺序)
观察变换：顶点变换的第二步，就是将顶点坐标从世界空间变换到观察空间中，这个变换通常叫做观察变换。一种方法是计算观察空间中的三个坐标轴在世界空间下的表示，然后构建出观察空间变换到世界空间的变换矩阵，再对该矩阵求逆得到从世界空间变换到观察空间的变换矩阵。另一种方法是想象平移整个观察空间，让摄像机原点位于世界坐标的原点，坐标轴与世界空间中的坐标轴重合即可
投影变换：顶点变换的第三步，就是将顶点坐标从观察空间变换到裁切空间(也被称为齐次裁剪空间)中，这个变换通常叫做投影变换，这个用于变换的矩阵叫做裁剪矩阵，也被称为投影矩阵。
- 目的：首先是为投影做准备，真正的投影发生在后面的齐次除法过程中，而经过投影矩阵变换后，顶点的w分量将会有特殊的意义；其次是对x,y,z分量进行缩放。
- 视椎体指的是空间中的一块区域，这块区域决定了摄像机可以看到的空间。视椎体由两种类型，这涉及两种投影：一种是正交投影，一种是透视投影。
- 投影：可以理解成一个空间的降维，例如从四维空间投影到三维空间，而投影矩阵实际上并不会真正的进行投影，它会为真正的投影做准备工作。真正的投影会在屏幕映射时发生，通过齐次除法来得到二维坐标。
屏幕映射：就是把顶点从裁剪空间投影到屏幕空间中，来生成对应的2D坐标。在unity中，从裁剪空间到屏幕空间的转换一般是底层帮我们完成的，我们顶点着色器只需要把顶点转换到裁剪空间即可。最后由此通过齐次除法和映射到屏幕。——分为两个步骤：首先进行标准齐次除法，也被称为透视除法。就是用齐次坐标系的w分量去除以x，y，z分量；经过齐次除法后，透视投影和正交投影的视椎体都变换到一个相同的立方体内。接下来可以根据变换后的x和y坐标来映射输出窗口的对应像素坐标。

unity中C#相关API

Transform.forward, Transform.right, Transform.up：当前物体的物体坐标系的z轴，x轴，y轴在世界坐标系上的指向。
Transform.TransformPoint(Vector3 position) :将一个坐标点从局部坐标系转换到全局坐标系。
Transform.InverseTransformPoint(Vector3 position)：将坐标点从全局坐标系转换到局部坐标系。
Transform.TransformDirection(Vector3 direction):将一个方向从局部坐标系转换到全局坐标系。
Transform.InverseTransformDirection(Vector3 direction)：将一个方向从全局坐标系转换到局部坐标系。
Transform.TransformVector(Vector3 vector):将一个向量从局部坐标系转换到全局坐标系。
Transform.InverseTransformVector(Vector3 vector):将一个向量从全局坐标系转换到局部坐标系。
Camera.ScreenToWorldPoint(Vector3 position): 将屏幕坐标转换为全局坐标。
Camera.WorldToScreenPoint(Vector3 position):将全局坐标转换为屏幕坐标。
Camera.ScreenToViewportPoint(Vector3 position)：将屏幕坐标转换为视口坐标。
Camera.ViewportToScreenPoint(Vector3 position)：将视口坐标转换为屏幕坐标。
Camera.WorldToViewportPoint(Vector3 position)：将全局坐标转换为视口坐标。
Camera.ViewportToWorldPoint(Vector3 position)：将视口坐标转换为全局坐标。

向量

认识向量

在数学中，向量（也称为矢量），是指具有大小和方向的量；书写向量时，水平书写的向量叫做行向量
$\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}$
垂直书写的向量叫做列向量。
$\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$
向量的大小就是向量的长度，也叫做模。向量的方向描述了空间中向量的指向；向量中的数表达了向量在每个维度上的有向位移。
点中的数表示了一个位置，它没有大小、方向的概念；点只有位置，适量只有方向和大小，任何一个点都可以表示成一个从原点出发的矢量。

向量运算

特殊向量

零向量：大小为0，没有方向的向量，并且它不可以被归一化。
负向量：向量变负,将得到一个和原向量方向相反、大小相等的向量。
单位向量：也叫做标准化向量，就是大小为1的向量；对任意的非零向量，我们都可以计算出它的单位向量，即将其归一化(normalization)。单位向量的表示
$\widehat{\bf{a}} =\frac{\bf{a}}{\begin{vmatrix} \bf{a} \end{vmatrix}}$
在Unity中，可以使用Vector3.Normalize来归一化向量。使用Vector3.normalized来获得归一化后的单位向量；Vector3.Normalize改变当前向量，Vector3.normalized当前向量是不改变的并且返回一个新的规范化的向量。

向量的长度

即向量的大小，或者向量的模。
向量的大小就是向量各分量平方和的平方根
在Unity中，可以通过Vector3.magnitude计算向量的长度。Vector3.sqrMagnitude则返回向量长度的平方；Vector3.Distance(A,B)可以计算2个点A,B之间的距离，即返回向量AB或向量BA的长度。

向量与标量的乘/除法

向量与标量的乘法，即将向量的每个分量分别与标量相乘。
向量与非零标量的除法，即乘以该标量的倒数。

向量的加/减法

只有在两个向量的维度相同时，才可以相加或相减。
向量的加法和减法，即将向量的各个分量相加或相减。
向量的加法满足交换律和结合律，向量的减法仅满足结合律。
几何意义：对于加法，我们可以把矢量a的头连接到矢量b的尾，然后画一条从a的尾到b的头的矢量，来得到a和b相加后的矢量。减法类似
公式： $\vec{a} + \vec{b}=(a_x+b_x,a_y+b_y,a_z+b_z) \\ \vec{a} - \vec{b}=(a_x-b_x,a_y-b_y,a_z-b_z)$

向量的点积

也叫做向量的内积。表示如下：其中点不可以省略
$\vec{a} \cdot \vec{b}$
两种计算公式如下：
$\vec{a} \cdot \vec{b}=\rvert \vec{a} \rvert \rvert \vec{b} \rvert \cos \theta \\ \vec{a} \cdot \vec{b}=(a_xb_x+a_yb_y+a_zb_z)$
点积满足交换律。
向量点积的结果是一个标量
几何意义：
- 点乘结果描述了两个向量的“相似”程度，点乘结果越大，两向量越相近
- 投影：向量b在向量a上的投影的长度可以表示为
  $\begin{vmatrix} \vec{b} \to \vec{a} \end{vmatrix}=\begin{vmatrix} \vec{b} \end{vmatrix} \cos \theta=\frac{\vec{a} \cdot \vec{b}}{\begin{vmatrix} \vec{a} \end{vmatrix}}$
重要性质：
- 点积可结合标量乘法
  $\vec{a}) \cdot \vec{b} = \vec{a} \cdot (k \vec{b})=k ( \vec{a} \cdot \vec{b})$
- 点积可结合矢量加减法
  $\vec{a} \cdot ( \vec{b}+\vec{c}) = \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}$
- 一个矢量和本身进行点积的结果是该矢量的模的平方

向量的叉积

也叫做向量的外积。表示如下：其中叉不可以省略
$\vec{a} \times \vec{b}$
计算公式如下：
$\begin{bmatrix} x_{1}\\ y_{1}\\ z_{1} \end{bmatrix}\times\begin{bmatrix} x_{2}\\ y_{2}\\ z_{2} \end{bmatrix} =\begin{bmatrix} y_{1}z_{2}-z_{1}y_{2}\\ z_{1}x_{2}-x_{1}z_{2}\\ x_{1}y_{2}-y_{1}x_{2} \end{bmatrix}$
三重积： $\vec{a} \cdot \vec{b} \times \vec{c}=\vec{a} \cdot (\vec{b} \times \vec{c})$
点积不满足交换律，也不满足结合律。
向量叉积的结果仍是一个向量
几何意义：
- 叉乘得到的向量垂直于原来的两个向量
- 叉乘的长度等于向量的大小与向量夹角sin值的积
  $\begin{vmatrix} \vec{a} \times \vec{b} \end{vmatrix} = \begin{vmatrix} \vec{a} \end{vmatrix} \begin{vmatrix} \vec{b} \end{vmatrix} \sin \theta$
- 叉乘的长度也等于以a和b为两边的平行四边形的面积

矩阵

认识矩阵

在数学中，矩阵是一个按照长方阵排列的复数或实数的集合。
在一个m×n的矩阵A中，有m×n个数，这些数称为矩阵A的元素。数 a_ij 位于矩阵的第i行，第j列，称为矩阵A的(i,j)元素。
矩阵中元素的下标是从1开始的。
$\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1j} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2j} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & a_{i3} & \cdots &a_{ij} \\ \end{bmatrix}$

矩阵和标量的乘法

矩阵和标量相乘，得到的仍然是一个相同维度的矩阵。矩阵和标量的乘法，即矩阵的每个元素和该标量相乘

矩阵和矩阵的加/减法

只有维度相同的矩阵，才可以相加相减
矩阵和矩阵的相加/相减即矩阵各相同位置的元素的相加相减

矩阵和矩阵的乘法

公式：一个r×n的矩阵A和一个n×c的矩阵B相乘，它们的结果AB将会是一个r×c大小的矩阵。这里第一个矩阵的列数必须和第二个矩阵的行数相同，他们相乘得到的矩阵的行数是第一个矩阵的行数，列数是第二个矩阵的列数。
演示：
矩阵乘法不满足交换律，但是满足结合律及以下关系： $\mathbf{AB}\neq \mathbf{BA} \\ \left ( \mathbf{AB} \right )\mathbf{C}= \mathbf{A}\left ( \mathbf{BC} \right ) \\ \mathbf{AB}= \mathbf{B^{T}A}$
矩阵的几何意义
1. 方阵的的行能被解释为坐标系的基向量；
2. 为了将向量从原坐标系变换到新坐标系，用它乘以一个矩阵；
3. 从原坐标系到这些基向量定义的新坐标系的变换是一种线性变换；线性变换保持直线和平行线，但角度、长度、面积和体积可能会被改变。
4. 零向量乘以任何矩阵仍然得到零向量。因此，方阵代表的线性变换的原点和原坐标系的原点一致，变换不包含原点。
5. 可以通过想象变换后的坐标系的基向量来想象矩阵，这些基向量在2D中构成“L”型，在3D中构成“三角架”型。

如何理解矩阵相乘的几何意义或现实意义？

向量和矩阵相乘：行向量左乘矩阵时，结果是行向量；列向量右乘矩阵时，结果是列向量，其他相乘顺序是不允许的。

特殊矩阵

方阵

行数和列数相等的矩阵被称为方块矩阵

对角矩阵

对角线元素：方阵中行号和列号相同的元素，其他元素为非对角线元素
如果一个矩阵除了对角元素外的所有元素都为0，那么这个矩阵就叫做对角矩阵

单位矩阵

对角线元素为1，其他元素为0。（乘法单位元）

转置矩阵

一个r×c矩阵M,M的转置记作 $\bf M^T$ 是一个c×r矩阵，它的列由M的行组成。即
$M_{ij}^{T}=M_{ji}$
性质1：矩阵转置的转置等于原矩阵：
$\left (\mathbf{M} ^{T}\right )^{T}=\mathbf{M}$
性质2：矩阵串接的转置等于反向串接各个矩阵的转置：
$\left ( \mathbf{AB} \right )^{T}=\mathbf{B}^{T}\mathbf{A}^{T}$

逆矩阵

给定一个方阵M，它的逆矩阵表示:
$\bf{M}^{-1}$
如果一个矩阵有相应的逆矩阵，则可以说这个矩阵是可逆的，或者说是非奇异的。如果一个矩阵没有相应的逆矩阵，则可以说这个矩阵是不可逆的，或者说是奇异的。
性质1：只有方块矩阵才可能有逆矩阵，因为一个矩阵A和它的逆矩阵B需要满足条件：AB = I(I是单位矩阵)。
$\mathbf{M}\mathbf{M}^{-1}=\mathbf{M}^{-1}\mathbf{M}=\mathbf{I}$
性质2：逆矩阵的逆矩阵是原矩阵本身。
$\left ( \mathbf{M}^{-1} \right )^{-1}=\mathbf{M}$
性质3：单位矩阵的逆矩阵是它本身
$\mathbf{I}^{-1}=\mathbf{I}$
性质4：转置矩阵的逆矩阵是逆矩阵的转置
$\left ( \mathbf{M}^{T} \right )^{-1}=\left ( \mathbf{M}^{-1} \right )^{T}$
性质5：矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵（这个性质可以扩展到更多矩阵相乘）
$\left ( \mathbf{AB} \right )^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1}$
对于所有元素都为0的矩阵，没有对应的逆矩阵。
?矩阵的逆的几何解释：如果向量v用矩阵M来进行变换，接着用M的逆进行变换，将会得到原向量。

正交矩阵

如果一个方阵M和它的转置矩阵的乘积是单位矩阵的话，我们就说这个矩阵是正交的： $\mathbf{M}\mathbf{M}^{T}=\mathbf{M}^{T}\mathbf{M}=\mathbf{I}$
推理：如果一个矩阵是正交的，那么它的转置矩阵和逆矩阵是一样的。
几何意义：若一个矩阵是正交矩阵，它必须满足下列条件：
1. 矩阵的每一行都是单位向量
2. 矩阵的所有行互相垂直
线性代数中一组向量互相垂直，这组向量被认为是正交基；如果他们同时满足都是单位向量，则称他们是标准正交基

矩阵的行列式

定义
- 在任意方阵中都存在一个标量，称作该方阵的行列式；非方阵的行列式是未定义的。
  在书写行列式时，两边用竖线将数字块围起来，省略方括号。
- 2D：帮助记忆法：将主对角线和反对角线上的元素各自相乘，然后用主对角线元素的积减去反对角线元素的积。
  $\left | M \right |=\begin{vmatrix} m_{11} &m_{12} \\ m_{21} & m_{22} \end{vmatrix}=m_{11}m_{22}-m_{12}m_{21}$
- 3D：帮助记忆法：把矩阵M连写两遍，将主对角线上的元素和反对角线上的元素各自相乘，然后用主对角线上元素积的和减去反对角线上元素积的和。
  $\left | M \right |=\begin{vmatrix} m_{11} & m_{12} &m_{13} \\ m_{21} & m_{22} &m_{23} \\ m_{31} & m_{32} &m_{33} \end{vmatrix}=m_{11}m_{22}m_{33}+m_{12}m_{23}m_{31}+m_{13}m_{21}m_{32}-m_{13}m_{22}m_{31}-m_{12}m_{21}m_{33}-m_{11}m_{23}m_{32}=m_{11}(m_{22}m_{33}-m_{23}m_{32})+m_{12}(m_{23}m_{31}-m_{21}m_{33})+m_{13}(m_{21}m_{32}-m_{22}m_{31})$
行列式的一些性质：
- 任意行或列的非零积加到另一行或列上不会改变行列式的值
- 交换矩阵的任意两行或两列，行列式变负
- 如果矩阵的任意行或列全为零，那么它的行列式等于零
- 矩阵积的行列式等于矩阵行列式的积；这个性质可以扩展到多个矩阵情况.
  $\left | AB \right |=\left| A \right|\left| B \right|$
- 矩阵转置的行列式等于原矩阵的行列式。
  $\left | M^{T} \right |=\left | M \right |$
矩阵的行列式的几何意义：
- 2D中，行列式等于以基向量为两边的平行四边形的有符号面积；（有符号面积是指如果平行四边形相对于远来的方位“翻转”，那么面积变负。）
- 3D中，行列式等于以变换后的基向量为三边的平行六面体的有符号体积，3D中，如果变换使得平行六面体“由里向外”翻转，则行列式变负。
- 行列式和矩阵变换导致的尺寸改变相关。其中行列式的绝对值和面积(2D)，体积(3D)的改变相关。行列式的符号说明了变换矩阵是否包含镜像或投影。
- 矩阵的行列式还可以对矩阵所代表的变换分类：如果矩阵行列式为零，那么该矩阵包含投影；如果矩阵行列式为负，那么该矩阵包含镜像。

变换

齐次坐标

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。

线性变换

定义：从代数上，是指可以保留矢量加和标量乘的变换。需要满足下面的2个条件。
$A(α+β)=A（α）+A（β）\\[1ex] A (kα)=kA(α)$
从几何的角度上去理解，需要满足：
1. 变换前是直线的，变换后依然是直线。
2. 直线比例保持不变。
3. 变换前是原点的，变换后依然是原点。
旋转和缩放都属于线性变换
1. 旋转
  2D旋转
  $R(\theta )=\begin{bmatrix} p^{'}\\ q^{'} \end{bmatrix}=\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$
  3D旋转
  绕X轴
  $R(\theta )=\begin{bmatrix} p^{'}\\ q^{'}\\ r^{'} \end{bmatrix}=\begin{bmatrix} 1&0&0 \\ 0&cos\theta&sin\theta \\ 0&-sin\theta&cos\theta \end{bmatrix}$
  绕Y轴
  $R(\theta )=\begin{bmatrix} p^{'}\\ q^{'}\\ r^{'} \end{bmatrix}=\begin{bmatrix} cos\theta&0&-sin\theta \\ 0&1&0 \\ sin\theta&0&cos\theta \end{bmatrix}$
  绕Z轴
  $R(\theta )=\begin{bmatrix} p^{'}\\ q^{'}\\ r^{'} \end{bmatrix}=\begin{bmatrix} cos\theta&sin\theta&0 \\ -sin\theta&cos\theta&0 \\ 0&0&1 \end{bmatrix}$
  2.缩放（沿着每个坐标轴应用单独的缩放因子k）
  2D缩放
  $S(k_{x},k_{y})=\begin{bmatrix} p^{'} \\ q^{'} \end{bmatrix}=\begin{bmatrix} k_{x} & 0\\ 0 & k_{y} \end{bmatrix}$
  3D缩放
  $S(k_{x},k_{y},k_{y})=\begin{bmatrix} p^{'} \\ q^{'} \\ r^{'} \end{bmatrix}=\begin{bmatrix} k_{x}&0&0 \\ 0&k_{y}&0 \\ 0&0&k_{z} \end{bmatrix}$

仿射变换

定义：从几何的角度去理解，需要满足：
1. 变换前是直线的，变换后依然是直线。
2. 直线比例保持不变。
推理：平移、旋转、缩放都属于仿射变换。
1. 对点平移
  $\begin{bmatrix} 1 & 0 & 0 & t_{x}\\ 0 & 1 & 0 & t_{y}\\ 0 & 0 & 1 & t_{z}\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}=\begin{bmatrix} x+t_{x}\\ y+t_{y}\\ z+t_{z}\\ 1 \end{bmatrix}$
2. 性质
  1、平移变换不会对方向矢量产生任何影响。
  2、平移矩阵的逆矩阵就是反向平移得到的矩阵
3. 复合变换
  由于上面我们使用的是列矩阵，因此阅读顺序是从右向左，即先缩放，在旋转，最后平移。顺序很重要。
透视投影
1. 将3D空间投影到2D平面上，该平面称作投影平面，使用的是正交投影。正交投影也称作平行投影；透视投影的投影线不再是平行的，它们相交于一点，该点称作投影中心。因为投影中心在投影平面前面，投影线到达平面之前已经相交，所以投影平面上的图像是翻转的。。。当物体原理投影中心时，正交投影仍保持不变，但透视投影变小了，这种视觉现象称作透视缩略。
2. 小孔成像：
  公式：(向z=d平面投影)
  ${p}'=\begin{bmatrix} {x}'\\ {y}'\\ {z}' \end{bmatrix}=\begin{bmatrix} dx/z\\ dy/z\\ d \end{bmatrix}$
  使用矩阵进行透视投影
  $\begin{bmatrix} x & y & z & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1/d\\ 0 & 0 & 0 & 0 \end{bmatrix}=\begin{bmatrix} x & y & z & z/d \end{bmatrix}$
unity相关API
1. 使用Matrix4x4.Translate创建一个平移矩阵。
2. 使用Matrix4x4.Rotate创建一个旋转矩阵。
3. 使用Matrix4x4.Scale创建一个缩放矩阵。
4. 使用Matrix4x4.TRS创建一个移动、旋转、缩放的复合矩阵。
5. 使用Matrix4x4.MultiplyPoint或者Matrix4x4.MultiplyPoint3x4来变换一个点。
6. 使用Matrix4x4.MultiplyVector来变换一个向量。